23.2.1 中心对称 人教版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 23.2.1 中心对称 人教版九年级数学上册课时作业(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 321.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 14:26:56 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册课时作业
第二十三章 旋转
23.2 中心对称
23.2.1 中心对称
1. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2. 若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是( )
A.AB=CD B.AB∥CD C.AB平行且等于CD D.不确定
3. 如图,在 ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有( )
A.4对 B.3对 C.2对 D.1对
4. 如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或4 B.2或3 C.3或4 D.1或2
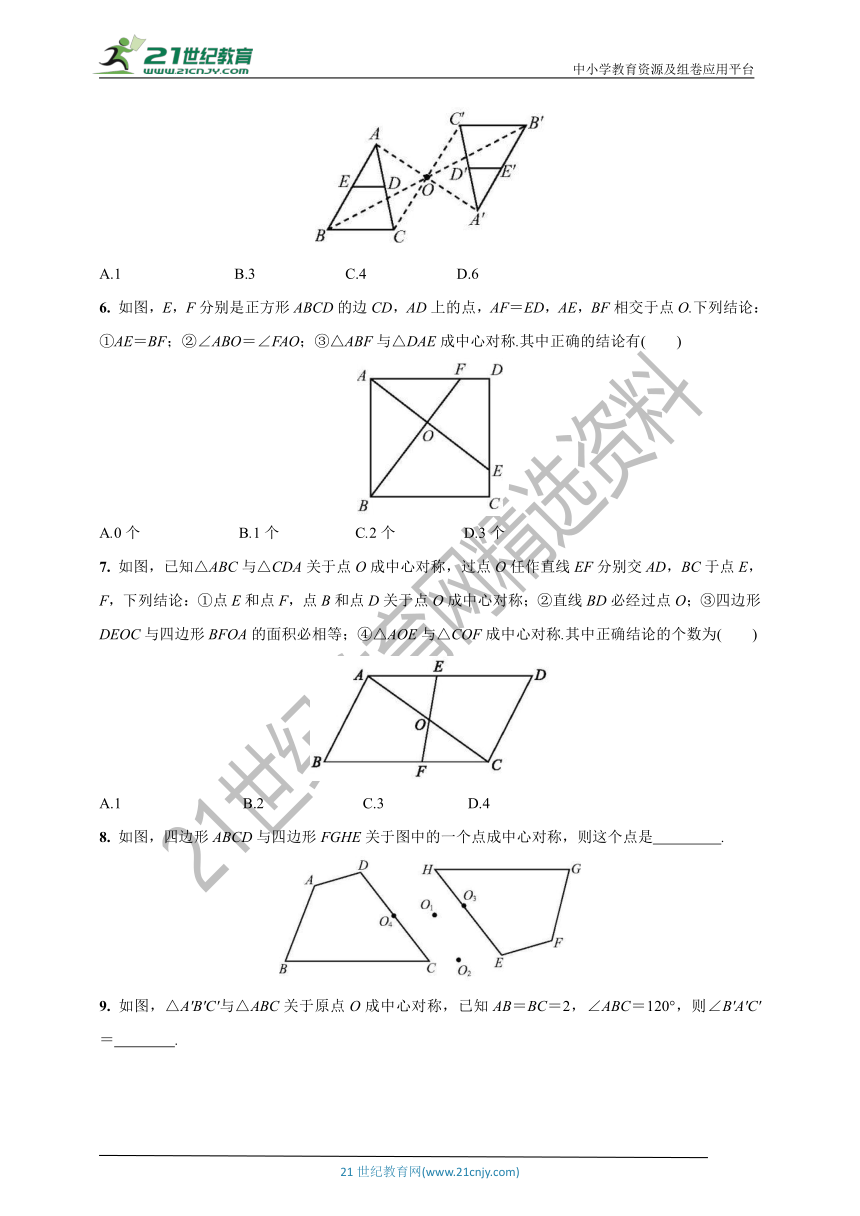
5. 如图,△ABC与△A'B'C'关于点O成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线.已知BC=6,则E'D'的长是( )
A.1 B.3 C.4 D.6
6. 如图,E,F分别是正方形ABCD的边CD,AD上的点,AF=ED,AE,BF相交于点O.下列结论:①AE=BF;②∠ABO=∠FAO;③△ABF与△DAE成中心对称.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
7. 如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
8. 如图,四边形ABCD与四边形FGHE关于图中的一个点成中心对称,则这个点是 .
9. 如图,△A'B'C'与△ABC关于原点O成中心对称,已知AB=BC=2,∠ABC=120°,则∠B'A'C'= .
10. 如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 .
11. 如图所示,已知△ABC和点O,请用尺规作出与△ABC关于点O对称的△A'B'C'.
12. 由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
13. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,-1),B(-1,-4),C(-3,-4).
(1)作出△A1B1C1,使△A1B1C1与△ABC关于y轴成轴对称图形;
(2)作出与△ABC关于原点成中心对称的图形△A2B2C2,并求出△A2B2C2的面积.
14. 课外兴趣小组活动时,老师提出了如下问题:
如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
解决问题:受到上述的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
图1 图2
参 考 答 案
1. C 2. C 3. A 4. D 5. B 6. C 7. D
8. O1
9. 30°
10. 2 DE的中点
11. 略
12. 解:如图所示.(答案不唯一)
13. 解:(1)图略.
(2)图略,△A2B2C2的面积=×3×2=3.
14. 解:(1)如图,延长FD到点G,使得DG=DF,连接BG,EG(或把△CFD绕点D逆时针旋转180°得到△BGD),∴CF=BG,DF=DG. 又∵DE⊥DF,∴EF=EG. 在△BEG中,BE+BG>EG,即BE+CF>EF.
(2)若∠A=90°,则∠EBC+∠FCB=90°,由(1)知∠FCB=∠DBG,EF=EG,∴∠EBC+∠DBG=90°,即∠EBG=90°,∴在Rt△EBG中,BE2+BG2=EG2,∴BE2+CF2=EF2.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学上册课时作业
第二十三章 旋转
23.2 中心对称
23.2.1 中心对称
1. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2. 若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是( )
A.AB=CD B.AB∥CD C.AB平行且等于CD D.不确定
3. 如图,在 ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有( )
A.4对 B.3对 C.2对 D.1对
4. 如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或4 B.2或3 C.3或4 D.1或2
5. 如图,△ABC与△A'B'C'关于点O成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线.已知BC=6,则E'D'的长是( )
A.1 B.3 C.4 D.6
6. 如图,E,F分别是正方形ABCD的边CD,AD上的点,AF=ED,AE,BF相交于点O.下列结论:①AE=BF;②∠ABO=∠FAO;③△ABF与△DAE成中心对称.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
7. 如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
8. 如图,四边形ABCD与四边形FGHE关于图中的一个点成中心对称,则这个点是 .
9. 如图,△A'B'C'与△ABC关于原点O成中心对称,已知AB=BC=2,∠ABC=120°,则∠B'A'C'= .
10. 如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 .
11. 如图所示,已知△ABC和点O,请用尺规作出与△ABC关于点O对称的△A'B'C'.
12. 由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
13. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,-1),B(-1,-4),C(-3,-4).
(1)作出△A1B1C1,使△A1B1C1与△ABC关于y轴成轴对称图形;
(2)作出与△ABC关于原点成中心对称的图形△A2B2C2,并求出△A2B2C2的面积.
14. 课外兴趣小组活动时,老师提出了如下问题:
如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2
解决问题:受到上述的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
图1 图2
参 考 答 案
1. C 2. C 3. A 4. D 5. B 6. C 7. D
8. O1
9. 30°
10. 2 DE的中点
11. 略
12. 解:如图所示.(答案不唯一)
13. 解:(1)图略.
(2)图略,△A2B2C2的面积=×3×2=3.
14. 解:(1)如图,延长FD到点G,使得DG=DF,连接BG,EG(或把△CFD绕点D逆时针旋转180°得到△BGD),∴CF=BG,DF=DG. 又∵DE⊥DF,∴EF=EG. 在△BEG中,BE+BG>EG,即BE+CF>EF.
(2)若∠A=90°,则∠EBC+∠FCB=90°,由(1)知∠FCB=∠DBG,EF=EG,∴∠EBC+∠DBG=90°,即∠EBG=90°,∴在Rt△EBG中,BE2+BG2=EG2,∴BE2+CF2=EF2.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
