2021-2022学年人教版数学七年级上册4.3.3余角和补角课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册4.3.3余角和补角课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 323.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 06:59:17 | ||
图片预览







文档简介
(共22张PPT)
七年级上册
4.3.3 余角和补角
学习目标
1.了解一个角的余角和补角的概念,能求出一个角的余角和补角;
2.经历探究互为余角和补角的性质的过程,并能简单应用;
3.了解方位角,能运用方位角确定物体的具体方位;
(打“√”或“×”)
(1)互余的两角一定相等.( )
(2)两个小于90°的角一定互余.( )
(3)若∠1<90°,则∠1的补角大于90°( )
(4)相等且互补的两个角分别等于90°.( )
(5)东南方向在东和南之间的任意一条射线上.( )
×
×
√
×
√
预习反馈
(1)在一副三角板中,每块都有一个角是90°,那么其余两个角的和是多少?它们有什么关系呢?
(2)观察方格如图中的两个角,你能猜想∠1+∠2等于多少度?它们有什么关系呢?
情境导入
1、余角的概念
如果两个角的和等于 ,就说这两个角互为余角,简称互余,即其中的一个角是另外一个角的余角.
如果∠1=30°,∠2=60°,我们可以说∠1与∠2互余,或者可以说∠1是∠2的余角,还可以说 .
90°
∠2是∠1的余角
课堂探究
如果两个角的和等于 ,就说这两个角互为补角,简称互补,即其中的一个角是另外一个角的补角.
2、补角的概念
如果∠1=45°,∠2=135°,我们可以说∠1与∠2互补,或者可以说∠1是∠2的补角,还可以说 .
180°
∠2是∠1的补角
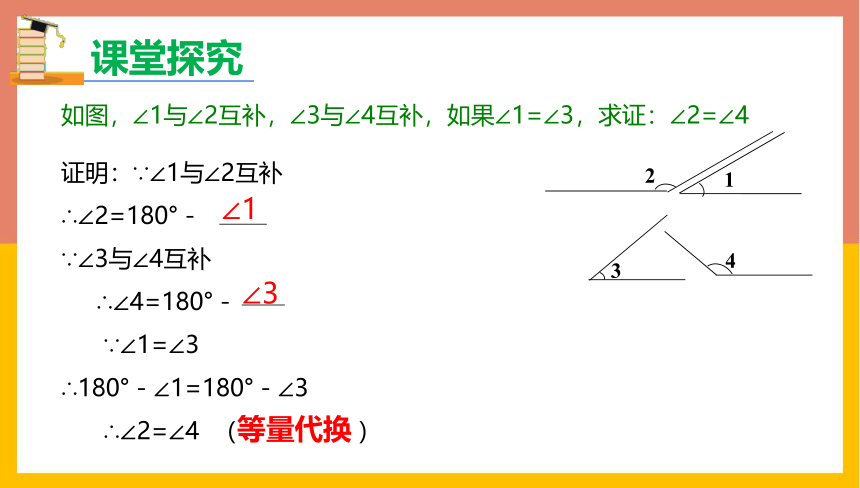
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,求证:∠2=∠4
证明:∵∠1与∠2互补
∴∠2=180°-
∵∠3与∠4互补
∴∠4=180°-
∵∠1=∠3
∴180°-∠1=180°-∠3
∴∠2=∠4 ( )
2
1
3
4
∠1
∠3
等量代换
课堂探究
归纳总结
由此,我们可以得到补角性质:
类似地,余角的性质:
同角(等角)的补角相等
同角(等角)的余角相等
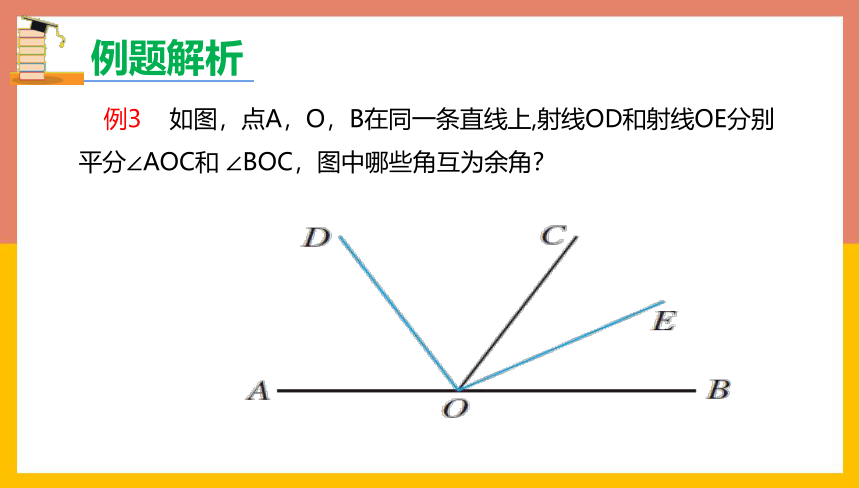
例3 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
例题解析
解: A,O,B在同一直线上,
∠AOC和∠BOC互为补角.
又 射线OD和射线OE分别平分∠AOC和∠BOC,
∠COD +∠COE= ∠AOC+ ∠BOC
= (∠AOC+ ∠BOC)
=90°
∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,∠COD 和∠BOE也互为余角.
方位角的概念
在生活当中,我们有时候需要用到角来描述方位,我们把这样的角称为方位角.方位角有时以______________________为基准,描述物体运动的方向.
正北或正南方向
方位角的表示习惯上以正北、正南方向为基准来描述物体的方向.即用“北偏东多少度”“北偏西多少度”或者“南偏东多少度”“南偏西多少度”来表示方向.
概念学习
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上,同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
例题解析
O
●
东
南
西
北
● A
60°
40°
B
C
10°
45°
D
画法 以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.
1.下列四个角中,最有可能与70°角互补的是( )
2.下列图形中,∠1和∠2互为余角的是( )
课堂练习
D
D
3.已知∠α=26°,则∠α的补角是____ 度.
4.一个角是35°39′,则它的余角为_______,补角为_______.
5.∠A与∠B互补,∠B与∠C互补,∠C=80°,则∠A的度数是________.
154
54°21′
144°21′
80°
6.∠A的余角和它的补角之比是1∶3,求∠A的度数.
解:设∠A的度数为x°,
则180-x=3(90-x),
解得x=45.
所以∠A的度数是45°.
7.如图,一只蚂蚁从O点出发,沿东北方向爬行2.5 cm碰到障碍物B后,折向北偏西60°的方向爬行3 cm到C.
(1)画出蚂蚁的爬行路线.
(2)求出∠OBC的度数.
解: (1)先以O为顶点,表示正北方向的射线为角的一边,画45°的角,使它的一边OB′落在东与北之间,在射线OB′上取OB等于2.5 cm,同理以B点为顶点,画出BC=3 cm,则OB,BC是蚂蚁所爬行的路线.
如图所示:
(2)由题意知,点O在点B的西南方向,
所以∠DBO=45°,
因为∠CBE=60°,所以∠CBD=30°,
所以∠OBC=∠CBD+∠DBO
=30°+45°=75°.
如果两个角的和等于90°,就说这两个角互为余角,简称互余,即其中的一个角是另外一个角的余角;
如果两个角的和等于180°,就说这两个角互为补角,简称互补,即其中的一个角是另外一个角的补角;
同角(等角)的补角相等
同角(等角)的余角相等
方位角是以正北、正南方向为基准,描述物体运动方向的角.
课堂小结
本节课我们学习了什么?你有什么收获呢?
布置作业
书面作业:完成相关书本作业
再见
七年级上册
4.3.3 余角和补角
学习目标
1.了解一个角的余角和补角的概念,能求出一个角的余角和补角;
2.经历探究互为余角和补角的性质的过程,并能简单应用;
3.了解方位角,能运用方位角确定物体的具体方位;
(打“√”或“×”)
(1)互余的两角一定相等.( )
(2)两个小于90°的角一定互余.( )
(3)若∠1<90°,则∠1的补角大于90°( )
(4)相等且互补的两个角分别等于90°.( )
(5)东南方向在东和南之间的任意一条射线上.( )
×
×
√
×
√
预习反馈
(1)在一副三角板中,每块都有一个角是90°,那么其余两个角的和是多少?它们有什么关系呢?
(2)观察方格如图中的两个角,你能猜想∠1+∠2等于多少度?它们有什么关系呢?
情境导入
1、余角的概念
如果两个角的和等于 ,就说这两个角互为余角,简称互余,即其中的一个角是另外一个角的余角.
如果∠1=30°,∠2=60°,我们可以说∠1与∠2互余,或者可以说∠1是∠2的余角,还可以说 .
90°
∠2是∠1的余角
课堂探究
如果两个角的和等于 ,就说这两个角互为补角,简称互补,即其中的一个角是另外一个角的补角.
2、补角的概念
如果∠1=45°,∠2=135°,我们可以说∠1与∠2互补,或者可以说∠1是∠2的补角,还可以说 .
180°
∠2是∠1的补角
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,求证:∠2=∠4
证明:∵∠1与∠2互补
∴∠2=180°-
∵∠3与∠4互补
∴∠4=180°-
∵∠1=∠3
∴180°-∠1=180°-∠3
∴∠2=∠4 ( )
2
1
3
4
∠1
∠3
等量代换
课堂探究
归纳总结
由此,我们可以得到补角性质:
类似地,余角的性质:
同角(等角)的补角相等
同角(等角)的余角相等
例3 如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
例题解析
解: A,O,B在同一直线上,
∠AOC和∠BOC互为补角.
又 射线OD和射线OE分别平分∠AOC和∠BOC,
∠COD +∠COE= ∠AOC+ ∠BOC
= (∠AOC+ ∠BOC)
=90°
∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,∠COD 和∠BOE也互为余角.
方位角的概念
在生活当中,我们有时候需要用到角来描述方位,我们把这样的角称为方位角.方位角有时以______________________为基准,描述物体运动的方向.
正北或正南方向
方位角的表示习惯上以正北、正南方向为基准来描述物体的方向.即用“北偏东多少度”“北偏西多少度”或者“南偏东多少度”“南偏西多少度”来表示方向.
概念学习
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上,同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
例题解析
O
●
东
南
西
北
● A
60°
40°
B
C
10°
45°
D
画法 以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.
1.下列四个角中,最有可能与70°角互补的是( )
2.下列图形中,∠1和∠2互为余角的是( )
课堂练习
D
D
3.已知∠α=26°,则∠α的补角是____ 度.
4.一个角是35°39′,则它的余角为_______,补角为_______.
5.∠A与∠B互补,∠B与∠C互补,∠C=80°,则∠A的度数是________.
154
54°21′
144°21′
80°
6.∠A的余角和它的补角之比是1∶3,求∠A的度数.
解:设∠A的度数为x°,
则180-x=3(90-x),
解得x=45.
所以∠A的度数是45°.
7.如图,一只蚂蚁从O点出发,沿东北方向爬行2.5 cm碰到障碍物B后,折向北偏西60°的方向爬行3 cm到C.
(1)画出蚂蚁的爬行路线.
(2)求出∠OBC的度数.
解: (1)先以O为顶点,表示正北方向的射线为角的一边,画45°的角,使它的一边OB′落在东与北之间,在射线OB′上取OB等于2.5 cm,同理以B点为顶点,画出BC=3 cm,则OB,BC是蚂蚁所爬行的路线.
如图所示:
(2)由题意知,点O在点B的西南方向,
所以∠DBO=45°,
因为∠CBE=60°,所以∠CBD=30°,
所以∠OBC=∠CBD+∠DBO
=30°+45°=75°.
如果两个角的和等于90°,就说这两个角互为余角,简称互余,即其中的一个角是另外一个角的余角;
如果两个角的和等于180°,就说这两个角互为补角,简称互补,即其中的一个角是另外一个角的补角;
同角(等角)的补角相等
同角(等角)的余角相等
方位角是以正北、正南方向为基准,描述物体运动方向的角.
课堂小结
本节课我们学习了什么?你有什么收获呢?
布置作业
书面作业:完成相关书本作业
再见
