2021-2022学年安徽省合肥市庐阳中学九年级(上)第一次段考数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年安徽省合肥市庐阳中学九年级(上)第一次段考数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 07:58:00 | ||
图片预览



文档简介
2021-2022学年安徽省合肥市庐阳中学九年级第一学期第一次段考数学试卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.抛物线y=x2﹣3x﹣4与y轴交点的坐标是( )
A.(0,4) B.(﹣4,0) C.(0,﹣4) D.(4,0)
2.抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为( )
A.y=x2+4x+3 B.y=x2+4x+5 C.y=x2﹣4x+3 D.y=x2﹣4x﹣5
3.对于二次函数y=﹣x2+x﹣4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(﹣2,﹣7)
D.图象与x轴有两个交点
4.把写成比例式,不正确的是( )
A. B. C. D.
5.下面四条线段中成比例线段的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,c=12
C.a=1,b=,c=,d= D.a=1,b=2,c=4,d=6
6.如图,在△ABC中,DE∥BC,AD=9,DB=3,CE=2,则AC的长为( )
A.6 B.7 C.8 D.9
7.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
A.﹣1<x<5 B.x>5 C.x<﹣1且x>5 D.x<﹣1或x>5
8.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么PB的长度为( )
A.cm B.cm C.cm D.cm
9.在同一坐标系中,函数y=kx+k和函数y=﹣kx2+3x+2(k是常数,且k≠0)的图象可能是( )
A. B.
C. D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫做整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W.例如当a=2时,区域W内的整点个数为1,若区域W内恰有7个整点,则a的取值范围是( )
A.2<a≤3 B.2≤a<3 C.3<a≤4 D.3≤a<4
二、填空题(本大题共4小题,每题5分,满分20分)
11.若,则= .
12.若A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=的图象上的点,且x1<x2<0<x3,则y1、y2、y3的大小关系是 .
13.如图,在平面直角坐标系中,点B在y轴上,AB=AO,反比例函数y=(x<0)的图象经过点A,若S△ABO=3,则k的值为 .
14.已知关于x的二次函数y=x2﹣2tx+2.
(1)若点M(t﹣3,m),N(t+5,n)在抛物线上,则m n(用“<”、“=”或“>”填空);
(2)P(x1,y1),Q(x2,y2)是抛物线上的任意两个点,若对于﹣1≤x1<3且x2=3,都有y1≤y2,则t的取值范围为 .
三、(本大题共2小题,每题8分,满分16分)
15.已知二次函数y=﹣x2+4x.
(1)用配方法求出该函数图象的顶点坐标和对称轴.
(2)在如图所示的平面直角坐标系中画出该函数的图象.
16.已知线段a,b,c满足,且a+2b+c=26.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
四、(本大题共2小题,每题8分,满分16分)
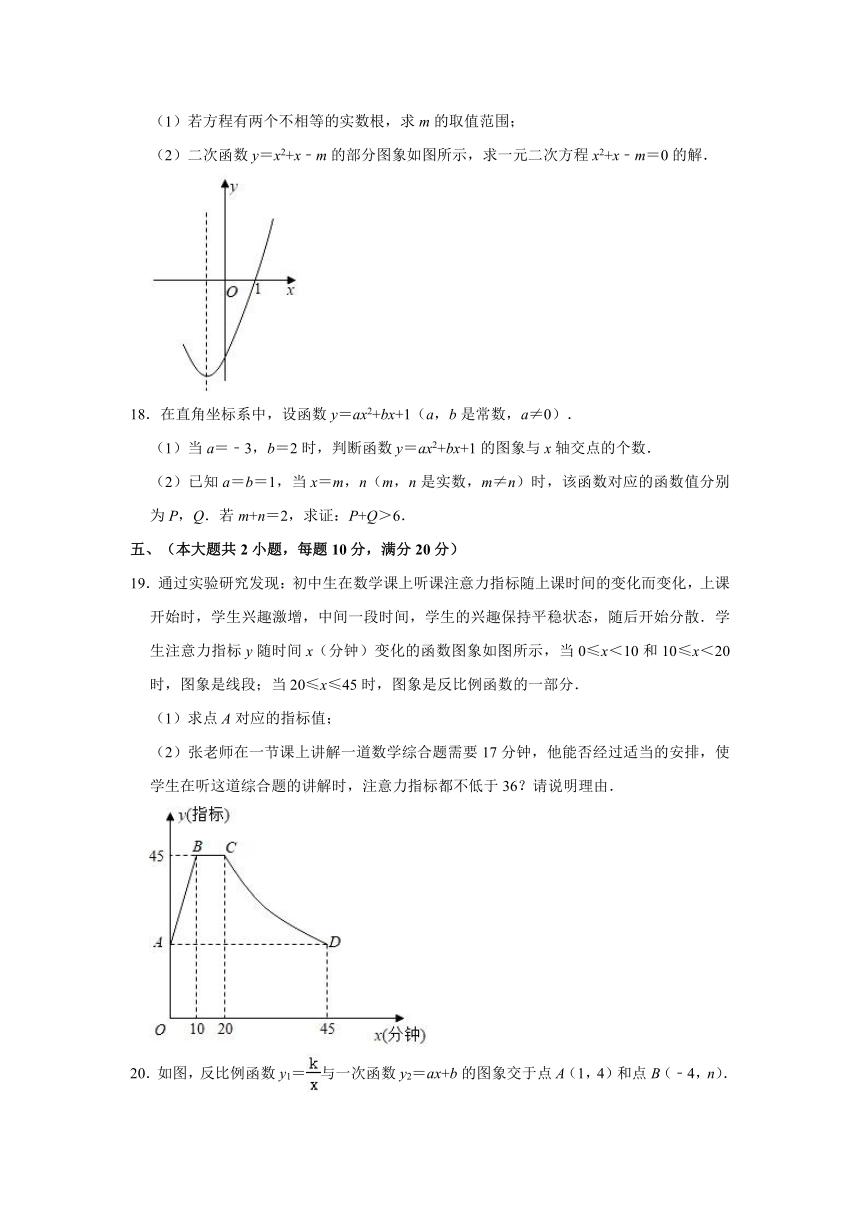
17.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
18.在直角坐标系中,设函数y=ax2+bx+1(a,b是常数,a≠0).
(1)当a=﹣3,b=2时,判断函数y=ax2+bx+1的图象与x轴交点的个数.
(2)已知a=b=1,当x=m,n(m,n是实数,m≠n)时,该函数对应的函数值分别为P,Q.若m+n=2,求证:P+Q>6.
五、(本大题共2小题,每题10分,满分20分)
19.通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
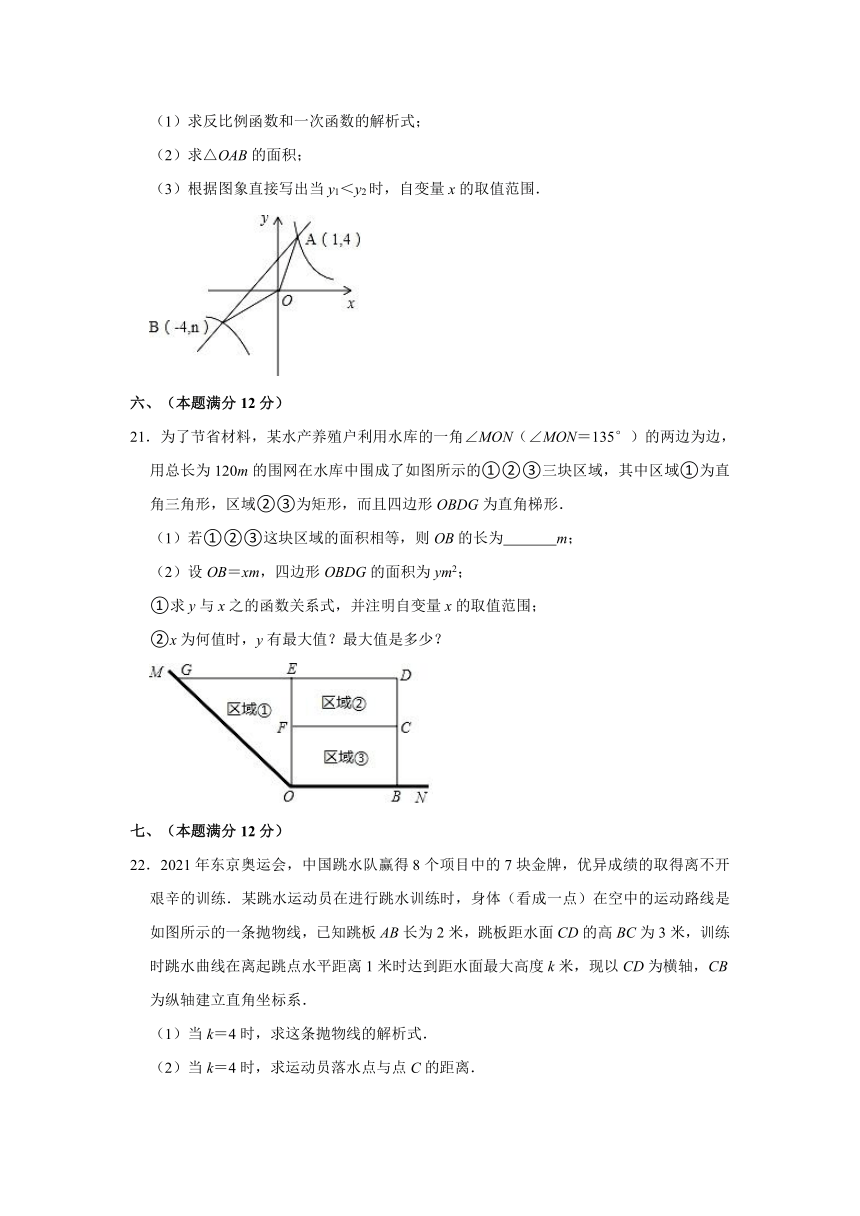
20.如图,反比例函数y1=与一次函数y2=ax+b的图象交于点A(1,4)和点B(﹣4,n).
(1)求反比例函数和一次函数的解析式;
(2)求△OAB的面积;
(3)根据图象直接写出当y1<y2时,自变量x的取值范围.
六、(本题满分12分)
21.为了节省材料,某水产养殖户利用水库的一角∠MON(∠MON=135°)的两边为边,用总长为120m的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形OBDG为直角梯形.
(1)若①②③这块区域的面积相等,则OB的长为 m;
(2)设OB=xm,四边形OBDG的面积为ym2;
①求y与x之的函数关系式,并注明自变量x的取值范围;
②x为何值时,y有最大值?最大值是多少?
七、(本题满分12分)
22.2021年东京奥运会,中国跳水队赢得8个项目中的7块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)当k=4时,求这条抛物线的解析式.
(2)当k=4时,求运动员落水点与点C的距离.
(3)图中CE=米,CF=5米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
八、(本题满分14分)
23.合肥市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:p=,日销售量y(千克)与时间第t(天)之间的函数关系如图所示.
(1)哪一天的日销售利润最大?最大利润是多少?
(2)该养殖户有多少天日销售利润不低于2400元?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
参考答案
一、选择题(本大题共10小题,每小题4分,共40分)
1.抛物线y=x2﹣3x﹣4与y轴交点的坐标是( )
A.(0,4) B.(﹣4,0) C.(0,﹣4) D.(4,0)
【分析】把x=0代入抛物线y=x2﹣3x﹣4,即得抛物线y=x2﹣3x﹣4与y轴的交点坐标.
解:把x=0代入抛物线y=x2﹣3x﹣4,得y=﹣4,
所以抛物线y=x2﹣3x﹣4与y轴的交点坐标为(0,﹣4).
故选:C.
2.抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为( )
A.y=x2+4x+3 B.y=x2+4x+5 C.y=x2﹣4x+3 D.y=x2﹣4x﹣5
【分析】抛物线平移不改变a的值.
解:原抛物线的顶点为(0,0),向左平移2个单位,再向下平移1个单位,那么新抛物线的顶点为(﹣2,﹣1).可设新抛物线的解析式为:y=(x﹣h)2+k,代入得:y=(x+2)2﹣1,化成一般形式得:y=x2+4x+3.故选A.
3.对于二次函数y=﹣x2+x﹣4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(﹣2,﹣7)
D.图象与x轴有两个交点
【分析】先用配方法把函数化为顶点式的形式,再根据其解析式即可求解.
解:∵二次函数y=﹣+x﹣4可化为y=﹣(x﹣2)2﹣3,
又∵a=﹣<0
∴当x=2时,二次函数y=﹣x2+x﹣4的最大值为﹣3.
故选:B.
4.把写成比例式,不正确的是( )
A. B. C. D.
【分析】把已知条件写成2ab=cd,再根据两内项之积等于两外项之积对各选项分析判断后利用排除法求解.
解:∵ab=cd,
∴2ab=cd,
A、∵=,
∴2ab=cd,故本选项不符合题意;
B、∵=,
∴ab=2cd,故本选项符合题意;
C、∵=,
∴2ab=cd,故本选项不符合题意;
D、∵=,
∴2ab=cd,故本选项不符合题意.
故选:B.
5.下面四条线段中成比例线段的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,c=12
C.a=1,b=,c=,d= D.a=1,b=2,c=4,d=6
【分析】根据成比例线段的概念,对选项进行一一分析,选出正确答案即可.
解:A、1×4≠2×3,故本选项不符合题意;
B、3×12≠6×9,故本选项不符合题意;
C、1×≠×,故本选项符合题意;
D、1×6≠2×4,故本选项不符合题意;
故选:C.
6.如图,在△ABC中,DE∥BC,AD=9,DB=3,CE=2,则AC的长为( )
A.6 B.7 C.8 D.9
【分析】利用平行线分线段成比例定理得到=,利用比例性质求出AE,然后计算AE+EC即可.
解:∵DE∥BC,
∴=,即=,
∴AE=6,
∴AC=AE+EC=6+2=8.
故选:C.
7.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
A.﹣1<x<5 B.x>5 C.x<﹣1且x>5 D.x<﹣1或x>5
【分析】先利用抛物线的对称性求出与x轴的另一个交点坐标,然后写出抛物线在x轴上方部分的x的取值范围即可.
解:由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点为(5,0),
所以,抛物线与x轴的另一个交点坐标为(﹣1,0),
所以,不等式ax2+bx+c>0的解集是﹣1<x<5.
故选:A.
8.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么PB的长度为( )
A.cm B.cm C.cm D.cm
【分析】先利用黄金分割的定义求出AP,再计算AB﹣AP即可得到PB的长度.
解:∵P为AB的黄金分割点(AP>PB),AB的长度为10cm,
∴AP=AB
=×10
=(5﹣5)cm,
∴PB=AB﹣AP
=10﹣(5﹣5)
=(15﹣5)cm,
故选:A.
9.在同一坐标系中,函数y=kx+k和函数y=﹣kx2+3x+2(k是常数,且k≠0)的图象可能是( )
A. B.
C. D.
【分析】分两种情况进行讨论:k>0与k<0进行讨论即可.
解:当k>0时,函数y=kx+k的图象经过一、二、三象限;函数y=﹣kx2+3x+2的开口向下,对称轴在y轴的右侧;
当k<0时,函数y=kx+k的图象经过二、三、四象限;函数y=﹣kx2+3x+2的开口向上,对称轴在y轴的左侧,故D正确.
故选:D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫做整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W.例如当a=2时,区域W内的整点个数为1,若区域W内恰有7个整点,则a的取值范围是( )
A.2<a≤3 B.2≤a<3 C.3<a≤4 D.3≤a<4
【分析】根据函数y=﹣x2+a(a>0)的图象对称性得出a的取值范围即可.
解:二次函数y=﹣x2+a(a>0)图象的顶点坐标为(0,a),由对称性可知,
当区域W内恰有7个整点时,这七个整数点坐标为(1,1)(1,2)(0,1)(0,2)(0,3)(﹣1,1)(﹣1,2),
因此a的取值范围为3<a≤4,
故选:D.
二、填空题(本大题共4小题,每题5分,满分20分)
11.若,则= .
【分析】由,得a=,代入所求的式子化简即可.
解:由,得a=,
∴=.
故答案为:.
12.若A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=的图象上的点,且x1<x2<0<x3,则y1、y2、y3的大小关系是 y2<y1<y3 .
【分析】首先根据函数关系式画出草图,然后根据图象可直接得到y1、y2、y3的大小关系.
解:如图所示:
∵x1<x2<0<x3,
∴y2<y1<y3.
故答案为:y2<y1<y3.
13.如图,在平面直角坐标系中,点B在y轴上,AB=AO,反比例函数y=(x<0)的图象经过点A,若S△ABO=3,则k的值为 ﹣3 .
【分析】如图,过点A作AD⊥y轴于点D,结合等腰三角形的性质得到△ADO的面积为1,所以根据反比例函数系数k的几何意义求得k的值.
解:如图,过点A作AD⊥y轴于点D,
∵AB=AO,△ABO的面积为3,
∴S△ADO=|k|=,
又反比例函数的图象位于第一象限,k<0,
则k=﹣3.
故答案为:﹣3.
14.已知关于x的二次函数y=x2﹣2tx+2.
(1)若点M(t﹣3,m),N(t+5,n)在抛物线上,则m < n(用“<”、“=”或“>”填空);
(2)P(x1,y1),Q(x2,y2)是抛物线上的任意两个点,若对于﹣1≤x1<3且x2=3,都有y1≤y2,则t的取值范围为 t≤1 .
【分析】(1)先求得开口方向和对称轴,然后根据二次函数的性质即可判断;
(2)当t≤1时,此时﹣1≤x1<3,x2=3都有y1≤y2,当t>1时,令x1=﹣1时,y1>y2,不符合题意,由此即可解决问题.
解:(1)∵y=x2﹣2tx+2=(x﹣t)2﹣t2+2.
∴抛物线开口向上,对称轴为直线x=t,
∴点M(t﹣3,m)关于对称轴的对称点为(t+3),
∵t<t+3<t+5,
∴m<n,
故答案为<;
(2)当t≤1时,此时﹣1≤x1<3,x2=3都有y1≤y2,符合题意;
当t>1时,令x1=﹣1时,y1>y2,不符合题意.
综上所述:t≤1;
故答案为:t≤1.
三、(本大题共2小题,每题8分,满分16分)
15.已知二次函数y=﹣x2+4x.
(1)用配方法求出该函数图象的顶点坐标和对称轴.
(2)在如图所示的平面直角坐标系中画出该函数的图象.
【分析】(1)用配方法把二次函数的解析式化为顶点式,从而求出函数的顶点和对称轴;
(2)用描点法画出函数图象.
解:(1)∵y=﹣x2+4x=﹣(x2﹣4x+4﹣4)=﹣(x﹣2)2+4,
∴顶点坐标为(2,4),对称轴为直线x=2;
(2)∵a=﹣1,
∴抛物线开口向下,
∵二次函数的常数项为0,
∴抛物线过原点,
∵对称轴为直线x=2,
∴抛物线过点(4,0),
函数图象如图所示:
16.已知线段a,b,c满足,且a+2b+c=26.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
【分析】(1)设===k,然后用k表示出a、b、c,再代入a+2b+c=26求解得到k,即可得到a、b、c的值;
(2)根据比例中项的定义列式得到m2=ab,即m2=4×6,然后根据算术平方根的定义求解.求解即可求出线段m的长.
解:(1)设===k,
则a=3k,b=2k,c=6k,
∵a+2b+c=26
∴3k+2×2k+6k=26,
解得k=2,
∴a=3×2=6,
b=2×2=4,
c=6×2=12;
(2)∵线段m是线段a、b的比例中项,
∴m2=ab=6×4=24,
∴m=2或m=﹣2(舍去),
∴线段m=2.
四、(本大题共2小题,每题8分,满分16分)
17.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
【分析】(1)由Δ>0即可列不等式得到答案;
(2)根据抛物线的对称性可得抛物线与x轴的另一个交点,即可得到答案.
解:(1)∵一元二次方程x2+x﹣m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,
∴m>﹣;
(2)二次函数y=x2+x﹣m图象的对称轴为直线x=﹣,
∴抛物线与x轴两个交点关于直线x=﹣对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
∴一元二次方程x2+x﹣m=0的解为x1=1,x2=﹣2.
18.在直角坐标系中,设函数y=ax2+bx+1(a,b是常数,a≠0).
(1)当a=﹣3,b=2时,判断函数y=ax2+bx+1的图象与x轴交点的个数.
(2)已知a=b=1,当x=m,n(m,n是实数,m≠n)时,该函数对应的函数值分别为P,Q.若m+n=2,求证:P+Q>6.
【分析】(1)将a=﹣3,b=2代入函数,然后通过Δ的符号求解.
(2)把a=b=1代入函数解析式,用含n代数式表示m,再用含m代数式表示P+Q,进而求解.
解:(1)∵a=﹣3,b=2,
∴y=﹣3x2+2x+1,
∵Δ=22+12=14>0,
∴抛物线与x轴有2个交点.
(2)∵a=b=1,
∴y=x2+x+1,
∴P=m2+m+1,Q=n2+n+1,
∴P+Q=m2+m+1+n2+n+1=m2+n2+m+n+2,
∵m+n=2,
∴n=2﹣m,
∴P+Q=m2+(2﹣m)2+4=2(m﹣1)2+6,
∵m≠n,
∴m≠1,
∴P+Q=2(m﹣1)2+6>6.
五、(本大题共2小题,每题10分,满分20分)
19.通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
【分析】(1)设反比例函数的解析式为y=,由C(20,45)求出k,可得D坐标,从而求出A的指标值;
(2)求出AB解析式,得到y≥36时,x≥,由反比例函数y=可得y≥36时,x≤25,根据25﹣=>17,即可得到答案.
解:(1)设当20≤x≤45时,反比例函数的解析式为y=,将C(20,45)代入得:
45=,解得k=900,
∴反比例函数的解析式为y=,
当x=45时,y==20,
∴D(45,20),
∴A(0,20),即A对应的指标值为20;
(2)设当0≤x<10时,AB的解析式为y=mx+n,将A(0,20)、B(10,45)代入得:
,解得,
∴AB的解析式为y=x+20,
当y≥36时,x+20≥36,解得x≥,
由(1)得反比例函数的解析式为y=,
当y≥36时,≥36,解得x≤25,
∴≤x≤25时,注意力指标都不低于36,
而25﹣=>17,
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36.
20.如图,反比例函数y1=与一次函数y2=ax+b的图象交于点A(1,4)和点B(﹣4,n).
(1)求反比例函数和一次函数的解析式;
(2)求△OAB的面积;
(3)根据图象直接写出当y1<y2时,自变量x的取值范围.
【分析】(1)把A(1,4)代入反比例函数y1=,得出k的值,再把B(﹣4,n)代入一次函数的解析式y2=ax+b,运用待定系数法分别求其解析式;
(2)设直线AB与y轴交于点C,把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算.
(3)根据A、B点的坐标即可求得自变量x的取值范围.
解:(1)∵A(1,4)在y1=上,
∴k=4.
∴反比例函数的解析式为y1=.
∵点B(﹣4,n)在y1=上,
∴n=﹣1.
∴B(﹣4,﹣1).
∵y2=ax+b经过A(1,4),B(﹣4,﹣1),
∴.
解得.
∴一次函数的解析式为y2=x+3.
(2)设C是直线AB与y轴的交点,
∴当x=0时,y=3.
∴点C(0,3).
∴OC=3.
∴S△AOB=S△ACO+S△BCO=×3×1+×3×4=.
(3)由图象可知;y1<y2时,自变量x的取值范围为;﹣4<x<0和x>1.
六、(本题满分12分)
21.为了节省材料,某水产养殖户利用水库的一角∠MON(∠MON=135°)的两边为边,用总长为120m的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形OBDG为直角梯形.
(1)若①②③这块区域的面积相等,则OB的长为 24 m;
(2)设OB=xm,四边形OBDG的面积为ym2;
①求y与x之的函数关系式,并注明自变量x的取值范围;
②x为何值时,y有最大值?最大值是多少?
【分析】(1)首先证明EG=EO=DB,DE=FC=OB,设OB=CF=DE=x,则GE=OE=BD=(120﹣2x)=40﹣x,由①②③这块区域的面积相等,得到(40﹣x)2= x(40﹣x),解方程即可.
(2)①由题意可知,∠MON=135°,∠EOB=∠D=∠DBO=90°,∠EGO=∠EOG=45°,CF=DE=OB=x,则GE=OE=BD=(120﹣2x)=40﹣x,则四边形OBDG的面积为y=S△GEO+S△OEBD.
②根据①中求得的解析式,利用配方法化为顶点式即可求最值.
解:(1)由题意可知,∠MON=135°,∠EOB=∠D=∠DBO=90°,
∴∠EGO=∠EOG=45°,
∴EG=EO=DB,DE=FC=OB,设OB=CF=DE=x,则GE=OE=BD=(120﹣2x)=40﹣x,
∵①②③这块区域的面积相等,
∴(40﹣x)2= x (40﹣x),
∴x=24或x=60(舍弃),
∴BO=24m.
故答案为24
(2)由题意可知,∠MON=135°,∠EOB=∠D=∠DBO=90°,
∴∠EGO=∠EOG=45°,
∴CF=DE=OB=x,则GE=OE=BD=(120﹣2x)=40﹣x
①四边形OBDG的面积为y=S△GEO+S△OEBD=,
整理得y=(0<x<60),
故y与x之的函数关系式为:y=(0<x<60),
②由①得,y与x之的函数关系式为:=,
∵<0
∴当x=15时,y有最大值,最大值为900.
七、(本题满分12分)
22.2021年东京奥运会,中国跳水队赢得8个项目中的7块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)当k=4时,求这条抛物线的解析式.
(2)当k=4时,求运动员落水点与点C的距离.
(3)图中CE=米,CF=5米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
【分析】(1)根据抛物线顶点坐标M(3,4),可设抛物线解析为:y=a(x﹣3)2+4,将点A(2,3)代入可得;
(2)在(1)中函数解析式中令y=0,求出x即可;
(3)若跳水运动员在区域EF内(含点E,F)入水达到训练要求,则在函数y=a(x﹣3)2+k中当x=米,y>0,当x=5米时y<0,解不等式即可得.
解:(1)如图所示:
根据题意,可得抛物线顶点坐标M(3,4),A(2,3),
设抛物线解析为:y=a(x﹣3)2+4,
则3=a(2﹣3)2+4,
解得:a=﹣1,
故抛物线解析式为:y=﹣(x﹣3)2+4;
(2)由题意可得:当y=0,则0=﹣(x﹣3)2+4,
解得:x1=1,x2=5,
故抛物线与x轴交点为:(5,0),
当k=4时,运动员落水点与点C的距离为5米;
(3)根据题意,抛物线解析式为:y=a(x﹣3)2+k,
将点A(2,3)代入可得:a+k=3,即a=3﹣k
若跳水运动员在区域EF内(含点E,F)入水,
则当x=时,y=a+k≥0,即(3﹣k)+k≥0,
解得:k≤,
当x=5时,y=4a+k≤0,即4(3﹣k)+k≤0,
解得:k≥4,
故4≤k≤.
八、(本题满分14分)
23.合肥市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:p=,日销售量y(千克)与时间第t(天)之间的函数关系如图所示.
(1)哪一天的日销售利润最大?最大利润是多少?
(2)该养殖户有多少天日销售利润不低于2400元?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
【分析】(1)设日销售量y与时间t的函数解析式为y=kt+b(k≠0),将(1,198)、(80,40)代入,得二元一次方程组,解得k和b的值,再代入y=kt+b即可;设日销售利润为w,根据日利润等于每千克的利润乘以日销售量可得w=(p﹣6)y,分两种情况讨论:①当1≤t≤40时,②当41≤t≤80时;
(2)令w=2400,即﹣(t﹣30)2+2450=2400,解一元二次方程组,求得解,并根据问题的实际意义及函数图象作出取舍;
(4)设日销售利润为w,根据题意,得:w=(t+16﹣6﹣m)(﹣2t+200),再根据前40天w随t的增大而增大,得出﹣×392+39(30+2m)+2000﹣200m<﹣×402+40(30+2m)+200﹣200m,即可得出结论.
解:(1)设日销售量y与时间t的函数解析式为y=kt+b(k≠0),
将(1,198)、(80,40)代入,得:
,
解得:,
∴y=﹣2t+200(1≤t≤80,t为整数);
设日销售利润为w,则w=(p﹣6)y,
①当1≤t≤40时,
w=(t+16﹣6)(﹣2t+200)=﹣(t﹣30)2+2450,
∵﹣<0,
∴当t=30时,w有最大值2450元;
②当41≤t≤80时,
w=(﹣t+46﹣6)(﹣2t+200)=(t﹣90)2﹣100,
∵1>0,
∴抛物线开口向上,
∴当t≤90时,w随t的增大而减小,
∵41≤t≤80,
∴当t=41时,w有最大值,最大值=(41﹣90)2﹣100=2301,
∵2450>2301,
∴第30天的日销售利润最大,最大利润为2 450元;
(2)由(1)得:当1≤t≤40时,
w=﹣(t﹣30)2+2450,
令w=2400,即﹣(t﹣30)2+2450=2400,
解得:t1=20,t2=40,
由函数w=﹣(t﹣30)2+2450图象可知,
当20≤t≤40时,日销售利润不低于2400元,
而当41≤t≤80时,w最大=2301<2400,
∴t的取值范围是20≤t≤40,
∴共有21天符合条件;
(3)设日销售利润为w,根据题意,得:
w=(t+16﹣6﹣m)(﹣2t+200)
=﹣t2+(30+2m)t+2000﹣200m,
由题意知,前40天,w随t的增大而增大,
﹣×392+39(30+2m)+2000﹣200m<﹣×402+40(30+2m)+200﹣200m,
解得:m>,
又m<7,
∴<m<7.
一、选择题(本大题共10小题,每小题4分,共40分)
1.抛物线y=x2﹣3x﹣4与y轴交点的坐标是( )
A.(0,4) B.(﹣4,0) C.(0,﹣4) D.(4,0)
2.抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为( )
A.y=x2+4x+3 B.y=x2+4x+5 C.y=x2﹣4x+3 D.y=x2﹣4x﹣5
3.对于二次函数y=﹣x2+x﹣4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(﹣2,﹣7)
D.图象与x轴有两个交点
4.把写成比例式,不正确的是( )
A. B. C. D.
5.下面四条线段中成比例线段的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,c=12
C.a=1,b=,c=,d= D.a=1,b=2,c=4,d=6
6.如图,在△ABC中,DE∥BC,AD=9,DB=3,CE=2,则AC的长为( )
A.6 B.7 C.8 D.9
7.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
A.﹣1<x<5 B.x>5 C.x<﹣1且x>5 D.x<﹣1或x>5
8.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么PB的长度为( )
A.cm B.cm C.cm D.cm
9.在同一坐标系中,函数y=kx+k和函数y=﹣kx2+3x+2(k是常数,且k≠0)的图象可能是( )
A. B.
C. D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫做整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W.例如当a=2时,区域W内的整点个数为1,若区域W内恰有7个整点,则a的取值范围是( )
A.2<a≤3 B.2≤a<3 C.3<a≤4 D.3≤a<4
二、填空题(本大题共4小题,每题5分,满分20分)
11.若,则= .
12.若A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=的图象上的点,且x1<x2<0<x3,则y1、y2、y3的大小关系是 .
13.如图,在平面直角坐标系中,点B在y轴上,AB=AO,反比例函数y=(x<0)的图象经过点A,若S△ABO=3,则k的值为 .
14.已知关于x的二次函数y=x2﹣2tx+2.
(1)若点M(t﹣3,m),N(t+5,n)在抛物线上,则m n(用“<”、“=”或“>”填空);
(2)P(x1,y1),Q(x2,y2)是抛物线上的任意两个点,若对于﹣1≤x1<3且x2=3,都有y1≤y2,则t的取值范围为 .
三、(本大题共2小题,每题8分,满分16分)
15.已知二次函数y=﹣x2+4x.
(1)用配方法求出该函数图象的顶点坐标和对称轴.
(2)在如图所示的平面直角坐标系中画出该函数的图象.
16.已知线段a,b,c满足,且a+2b+c=26.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
四、(本大题共2小题,每题8分,满分16分)
17.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
18.在直角坐标系中,设函数y=ax2+bx+1(a,b是常数,a≠0).
(1)当a=﹣3,b=2时,判断函数y=ax2+bx+1的图象与x轴交点的个数.
(2)已知a=b=1,当x=m,n(m,n是实数,m≠n)时,该函数对应的函数值分别为P,Q.若m+n=2,求证:P+Q>6.
五、(本大题共2小题,每题10分,满分20分)
19.通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
20.如图,反比例函数y1=与一次函数y2=ax+b的图象交于点A(1,4)和点B(﹣4,n).
(1)求反比例函数和一次函数的解析式;
(2)求△OAB的面积;
(3)根据图象直接写出当y1<y2时,自变量x的取值范围.
六、(本题满分12分)
21.为了节省材料,某水产养殖户利用水库的一角∠MON(∠MON=135°)的两边为边,用总长为120m的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形OBDG为直角梯形.
(1)若①②③这块区域的面积相等,则OB的长为 m;
(2)设OB=xm,四边形OBDG的面积为ym2;
①求y与x之的函数关系式,并注明自变量x的取值范围;
②x为何值时,y有最大值?最大值是多少?
七、(本题满分12分)
22.2021年东京奥运会,中国跳水队赢得8个项目中的7块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)当k=4时,求这条抛物线的解析式.
(2)当k=4时,求运动员落水点与点C的距离.
(3)图中CE=米,CF=5米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
八、(本题满分14分)
23.合肥市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:p=,日销售量y(千克)与时间第t(天)之间的函数关系如图所示.
(1)哪一天的日销售利润最大?最大利润是多少?
(2)该养殖户有多少天日销售利润不低于2400元?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
参考答案
一、选择题(本大题共10小题,每小题4分,共40分)
1.抛物线y=x2﹣3x﹣4与y轴交点的坐标是( )
A.(0,4) B.(﹣4,0) C.(0,﹣4) D.(4,0)
【分析】把x=0代入抛物线y=x2﹣3x﹣4,即得抛物线y=x2﹣3x﹣4与y轴的交点坐标.
解:把x=0代入抛物线y=x2﹣3x﹣4,得y=﹣4,
所以抛物线y=x2﹣3x﹣4与y轴的交点坐标为(0,﹣4).
故选:C.
2.抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为( )
A.y=x2+4x+3 B.y=x2+4x+5 C.y=x2﹣4x+3 D.y=x2﹣4x﹣5
【分析】抛物线平移不改变a的值.
解:原抛物线的顶点为(0,0),向左平移2个单位,再向下平移1个单位,那么新抛物线的顶点为(﹣2,﹣1).可设新抛物线的解析式为:y=(x﹣h)2+k,代入得:y=(x+2)2﹣1,化成一般形式得:y=x2+4x+3.故选A.
3.对于二次函数y=﹣x2+x﹣4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(﹣2,﹣7)
D.图象与x轴有两个交点
【分析】先用配方法把函数化为顶点式的形式,再根据其解析式即可求解.
解:∵二次函数y=﹣+x﹣4可化为y=﹣(x﹣2)2﹣3,
又∵a=﹣<0
∴当x=2时,二次函数y=﹣x2+x﹣4的最大值为﹣3.
故选:B.
4.把写成比例式,不正确的是( )
A. B. C. D.
【分析】把已知条件写成2ab=cd,再根据两内项之积等于两外项之积对各选项分析判断后利用排除法求解.
解:∵ab=cd,
∴2ab=cd,
A、∵=,
∴2ab=cd,故本选项不符合题意;
B、∵=,
∴ab=2cd,故本选项符合题意;
C、∵=,
∴2ab=cd,故本选项不符合题意;
D、∵=,
∴2ab=cd,故本选项不符合题意.
故选:B.
5.下面四条线段中成比例线段的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,c=12
C.a=1,b=,c=,d= D.a=1,b=2,c=4,d=6
【分析】根据成比例线段的概念,对选项进行一一分析,选出正确答案即可.
解:A、1×4≠2×3,故本选项不符合题意;
B、3×12≠6×9,故本选项不符合题意;
C、1×≠×,故本选项符合题意;
D、1×6≠2×4,故本选项不符合题意;
故选:C.
6.如图,在△ABC中,DE∥BC,AD=9,DB=3,CE=2,则AC的长为( )
A.6 B.7 C.8 D.9
【分析】利用平行线分线段成比例定理得到=,利用比例性质求出AE,然后计算AE+EC即可.
解:∵DE∥BC,
∴=,即=,
∴AE=6,
∴AC=AE+EC=6+2=8.
故选:C.
7.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
A.﹣1<x<5 B.x>5 C.x<﹣1且x>5 D.x<﹣1或x>5
【分析】先利用抛物线的对称性求出与x轴的另一个交点坐标,然后写出抛物线在x轴上方部分的x的取值范围即可.
解:由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点为(5,0),
所以,抛物线与x轴的另一个交点坐标为(﹣1,0),
所以,不等式ax2+bx+c>0的解集是﹣1<x<5.
故选:A.
8.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么PB的长度为( )
A.cm B.cm C.cm D.cm
【分析】先利用黄金分割的定义求出AP,再计算AB﹣AP即可得到PB的长度.
解:∵P为AB的黄金分割点(AP>PB),AB的长度为10cm,
∴AP=AB
=×10
=(5﹣5)cm,
∴PB=AB﹣AP
=10﹣(5﹣5)
=(15﹣5)cm,
故选:A.
9.在同一坐标系中,函数y=kx+k和函数y=﹣kx2+3x+2(k是常数,且k≠0)的图象可能是( )
A. B.
C. D.
【分析】分两种情况进行讨论:k>0与k<0进行讨论即可.
解:当k>0时,函数y=kx+k的图象经过一、二、三象限;函数y=﹣kx2+3x+2的开口向下,对称轴在y轴的右侧;
当k<0时,函数y=kx+k的图象经过二、三、四象限;函数y=﹣kx2+3x+2的开口向上,对称轴在y轴的左侧,故D正确.
故选:D.
10.在平面直角坐标系中,横、纵坐标都是整数的点叫做整点,记函数y=﹣x2+a(a>0)的图象在x轴上方的部分与x轴围成的区域(不含边界)为W.例如当a=2时,区域W内的整点个数为1,若区域W内恰有7个整点,则a的取值范围是( )
A.2<a≤3 B.2≤a<3 C.3<a≤4 D.3≤a<4
【分析】根据函数y=﹣x2+a(a>0)的图象对称性得出a的取值范围即可.
解:二次函数y=﹣x2+a(a>0)图象的顶点坐标为(0,a),由对称性可知,
当区域W内恰有7个整点时,这七个整数点坐标为(1,1)(1,2)(0,1)(0,2)(0,3)(﹣1,1)(﹣1,2),
因此a的取值范围为3<a≤4,
故选:D.
二、填空题(本大题共4小题,每题5分,满分20分)
11.若,则= .
【分析】由,得a=,代入所求的式子化简即可.
解:由,得a=,
∴=.
故答案为:.
12.若A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=的图象上的点,且x1<x2<0<x3,则y1、y2、y3的大小关系是 y2<y1<y3 .
【分析】首先根据函数关系式画出草图,然后根据图象可直接得到y1、y2、y3的大小关系.
解:如图所示:
∵x1<x2<0<x3,
∴y2<y1<y3.
故答案为:y2<y1<y3.
13.如图,在平面直角坐标系中,点B在y轴上,AB=AO,反比例函数y=(x<0)的图象经过点A,若S△ABO=3,则k的值为 ﹣3 .
【分析】如图,过点A作AD⊥y轴于点D,结合等腰三角形的性质得到△ADO的面积为1,所以根据反比例函数系数k的几何意义求得k的值.
解:如图,过点A作AD⊥y轴于点D,
∵AB=AO,△ABO的面积为3,
∴S△ADO=|k|=,
又反比例函数的图象位于第一象限,k<0,
则k=﹣3.
故答案为:﹣3.
14.已知关于x的二次函数y=x2﹣2tx+2.
(1)若点M(t﹣3,m),N(t+5,n)在抛物线上,则m < n(用“<”、“=”或“>”填空);
(2)P(x1,y1),Q(x2,y2)是抛物线上的任意两个点,若对于﹣1≤x1<3且x2=3,都有y1≤y2,则t的取值范围为 t≤1 .
【分析】(1)先求得开口方向和对称轴,然后根据二次函数的性质即可判断;
(2)当t≤1时,此时﹣1≤x1<3,x2=3都有y1≤y2,当t>1时,令x1=﹣1时,y1>y2,不符合题意,由此即可解决问题.
解:(1)∵y=x2﹣2tx+2=(x﹣t)2﹣t2+2.
∴抛物线开口向上,对称轴为直线x=t,
∴点M(t﹣3,m)关于对称轴的对称点为(t+3),
∵t<t+3<t+5,
∴m<n,
故答案为<;
(2)当t≤1时,此时﹣1≤x1<3,x2=3都有y1≤y2,符合题意;
当t>1时,令x1=﹣1时,y1>y2,不符合题意.
综上所述:t≤1;
故答案为:t≤1.
三、(本大题共2小题,每题8分,满分16分)
15.已知二次函数y=﹣x2+4x.
(1)用配方法求出该函数图象的顶点坐标和对称轴.
(2)在如图所示的平面直角坐标系中画出该函数的图象.
【分析】(1)用配方法把二次函数的解析式化为顶点式,从而求出函数的顶点和对称轴;
(2)用描点法画出函数图象.
解:(1)∵y=﹣x2+4x=﹣(x2﹣4x+4﹣4)=﹣(x﹣2)2+4,
∴顶点坐标为(2,4),对称轴为直线x=2;
(2)∵a=﹣1,
∴抛物线开口向下,
∵二次函数的常数项为0,
∴抛物线过原点,
∵对称轴为直线x=2,
∴抛物线过点(4,0),
函数图象如图所示:
16.已知线段a,b,c满足,且a+2b+c=26.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
【分析】(1)设===k,然后用k表示出a、b、c,再代入a+2b+c=26求解得到k,即可得到a、b、c的值;
(2)根据比例中项的定义列式得到m2=ab,即m2=4×6,然后根据算术平方根的定义求解.求解即可求出线段m的长.
解:(1)设===k,
则a=3k,b=2k,c=6k,
∵a+2b+c=26
∴3k+2×2k+6k=26,
解得k=2,
∴a=3×2=6,
b=2×2=4,
c=6×2=12;
(2)∵线段m是线段a、b的比例中项,
∴m2=ab=6×4=24,
∴m=2或m=﹣2(舍去),
∴线段m=2.
四、(本大题共2小题,每题8分,满分16分)
17.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
【分析】(1)由Δ>0即可列不等式得到答案;
(2)根据抛物线的对称性可得抛物线与x轴的另一个交点,即可得到答案.
解:(1)∵一元二次方程x2+x﹣m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,
∴m>﹣;
(2)二次函数y=x2+x﹣m图象的对称轴为直线x=﹣,
∴抛物线与x轴两个交点关于直线x=﹣对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
∴一元二次方程x2+x﹣m=0的解为x1=1,x2=﹣2.
18.在直角坐标系中,设函数y=ax2+bx+1(a,b是常数,a≠0).
(1)当a=﹣3,b=2时,判断函数y=ax2+bx+1的图象与x轴交点的个数.
(2)已知a=b=1,当x=m,n(m,n是实数,m≠n)时,该函数对应的函数值分别为P,Q.若m+n=2,求证:P+Q>6.
【分析】(1)将a=﹣3,b=2代入函数,然后通过Δ的符号求解.
(2)把a=b=1代入函数解析式,用含n代数式表示m,再用含m代数式表示P+Q,进而求解.
解:(1)∵a=﹣3,b=2,
∴y=﹣3x2+2x+1,
∵Δ=22+12=14>0,
∴抛物线与x轴有2个交点.
(2)∵a=b=1,
∴y=x2+x+1,
∴P=m2+m+1,Q=n2+n+1,
∴P+Q=m2+m+1+n2+n+1=m2+n2+m+n+2,
∵m+n=2,
∴n=2﹣m,
∴P+Q=m2+(2﹣m)2+4=2(m﹣1)2+6,
∵m≠n,
∴m≠1,
∴P+Q=2(m﹣1)2+6>6.
五、(本大题共2小题,每题10分,满分20分)
19.通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
【分析】(1)设反比例函数的解析式为y=,由C(20,45)求出k,可得D坐标,从而求出A的指标值;
(2)求出AB解析式,得到y≥36时,x≥,由反比例函数y=可得y≥36时,x≤25,根据25﹣=>17,即可得到答案.
解:(1)设当20≤x≤45时,反比例函数的解析式为y=,将C(20,45)代入得:
45=,解得k=900,
∴反比例函数的解析式为y=,
当x=45时,y==20,
∴D(45,20),
∴A(0,20),即A对应的指标值为20;
(2)设当0≤x<10时,AB的解析式为y=mx+n,将A(0,20)、B(10,45)代入得:
,解得,
∴AB的解析式为y=x+20,
当y≥36时,x+20≥36,解得x≥,
由(1)得反比例函数的解析式为y=,
当y≥36时,≥36,解得x≤25,
∴≤x≤25时,注意力指标都不低于36,
而25﹣=>17,
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36.
20.如图,反比例函数y1=与一次函数y2=ax+b的图象交于点A(1,4)和点B(﹣4,n).
(1)求反比例函数和一次函数的解析式;
(2)求△OAB的面积;
(3)根据图象直接写出当y1<y2时,自变量x的取值范围.
【分析】(1)把A(1,4)代入反比例函数y1=,得出k的值,再把B(﹣4,n)代入一次函数的解析式y2=ax+b,运用待定系数法分别求其解析式;
(2)设直线AB与y轴交于点C,把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算.
(3)根据A、B点的坐标即可求得自变量x的取值范围.
解:(1)∵A(1,4)在y1=上,
∴k=4.
∴反比例函数的解析式为y1=.
∵点B(﹣4,n)在y1=上,
∴n=﹣1.
∴B(﹣4,﹣1).
∵y2=ax+b经过A(1,4),B(﹣4,﹣1),
∴.
解得.
∴一次函数的解析式为y2=x+3.
(2)设C是直线AB与y轴的交点,
∴当x=0时,y=3.
∴点C(0,3).
∴OC=3.
∴S△AOB=S△ACO+S△BCO=×3×1+×3×4=.
(3)由图象可知;y1<y2时,自变量x的取值范围为;﹣4<x<0和x>1.
六、(本题满分12分)
21.为了节省材料,某水产养殖户利用水库的一角∠MON(∠MON=135°)的两边为边,用总长为120m的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形OBDG为直角梯形.
(1)若①②③这块区域的面积相等,则OB的长为 24 m;
(2)设OB=xm,四边形OBDG的面积为ym2;
①求y与x之的函数关系式,并注明自变量x的取值范围;
②x为何值时,y有最大值?最大值是多少?
【分析】(1)首先证明EG=EO=DB,DE=FC=OB,设OB=CF=DE=x,则GE=OE=BD=(120﹣2x)=40﹣x,由①②③这块区域的面积相等,得到(40﹣x)2= x(40﹣x),解方程即可.
(2)①由题意可知,∠MON=135°,∠EOB=∠D=∠DBO=90°,∠EGO=∠EOG=45°,CF=DE=OB=x,则GE=OE=BD=(120﹣2x)=40﹣x,则四边形OBDG的面积为y=S△GEO+S△OEBD.
②根据①中求得的解析式,利用配方法化为顶点式即可求最值.
解:(1)由题意可知,∠MON=135°,∠EOB=∠D=∠DBO=90°,
∴∠EGO=∠EOG=45°,
∴EG=EO=DB,DE=FC=OB,设OB=CF=DE=x,则GE=OE=BD=(120﹣2x)=40﹣x,
∵①②③这块区域的面积相等,
∴(40﹣x)2= x (40﹣x),
∴x=24或x=60(舍弃),
∴BO=24m.
故答案为24
(2)由题意可知,∠MON=135°,∠EOB=∠D=∠DBO=90°,
∴∠EGO=∠EOG=45°,
∴CF=DE=OB=x,则GE=OE=BD=(120﹣2x)=40﹣x
①四边形OBDG的面积为y=S△GEO+S△OEBD=,
整理得y=(0<x<60),
故y与x之的函数关系式为:y=(0<x<60),
②由①得,y与x之的函数关系式为:=,
∵<0
∴当x=15时,y有最大值,最大值为900.
七、(本题满分12分)
22.2021年东京奥运会,中国跳水队赢得8个项目中的7块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)当k=4时,求这条抛物线的解析式.
(2)当k=4时,求运动员落水点与点C的距离.
(3)图中CE=米,CF=5米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
【分析】(1)根据抛物线顶点坐标M(3,4),可设抛物线解析为:y=a(x﹣3)2+4,将点A(2,3)代入可得;
(2)在(1)中函数解析式中令y=0,求出x即可;
(3)若跳水运动员在区域EF内(含点E,F)入水达到训练要求,则在函数y=a(x﹣3)2+k中当x=米,y>0,当x=5米时y<0,解不等式即可得.
解:(1)如图所示:
根据题意,可得抛物线顶点坐标M(3,4),A(2,3),
设抛物线解析为:y=a(x﹣3)2+4,
则3=a(2﹣3)2+4,
解得:a=﹣1,
故抛物线解析式为:y=﹣(x﹣3)2+4;
(2)由题意可得:当y=0,则0=﹣(x﹣3)2+4,
解得:x1=1,x2=5,
故抛物线与x轴交点为:(5,0),
当k=4时,运动员落水点与点C的距离为5米;
(3)根据题意,抛物线解析式为:y=a(x﹣3)2+k,
将点A(2,3)代入可得:a+k=3,即a=3﹣k
若跳水运动员在区域EF内(含点E,F)入水,
则当x=时,y=a+k≥0,即(3﹣k)+k≥0,
解得:k≤,
当x=5时,y=4a+k≤0,即4(3﹣k)+k≤0,
解得:k≥4,
故4≤k≤.
八、(本题满分14分)
23.合肥市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:p=,日销售量y(千克)与时间第t(天)之间的函数关系如图所示.
(1)哪一天的日销售利润最大?最大利润是多少?
(2)该养殖户有多少天日销售利润不低于2400元?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
【分析】(1)设日销售量y与时间t的函数解析式为y=kt+b(k≠0),将(1,198)、(80,40)代入,得二元一次方程组,解得k和b的值,再代入y=kt+b即可;设日销售利润为w,根据日利润等于每千克的利润乘以日销售量可得w=(p﹣6)y,分两种情况讨论:①当1≤t≤40时,②当41≤t≤80时;
(2)令w=2400,即﹣(t﹣30)2+2450=2400,解一元二次方程组,求得解,并根据问题的实际意义及函数图象作出取舍;
(4)设日销售利润为w,根据题意,得:w=(t+16﹣6﹣m)(﹣2t+200),再根据前40天w随t的增大而增大,得出﹣×392+39(30+2m)+2000﹣200m<﹣×402+40(30+2m)+200﹣200m,即可得出结论.
解:(1)设日销售量y与时间t的函数解析式为y=kt+b(k≠0),
将(1,198)、(80,40)代入,得:
,
解得:,
∴y=﹣2t+200(1≤t≤80,t为整数);
设日销售利润为w,则w=(p﹣6)y,
①当1≤t≤40时,
w=(t+16﹣6)(﹣2t+200)=﹣(t﹣30)2+2450,
∵﹣<0,
∴当t=30时,w有最大值2450元;
②当41≤t≤80时,
w=(﹣t+46﹣6)(﹣2t+200)=(t﹣90)2﹣100,
∵1>0,
∴抛物线开口向上,
∴当t≤90时,w随t的增大而减小,
∵41≤t≤80,
∴当t=41时,w有最大值,最大值=(41﹣90)2﹣100=2301,
∵2450>2301,
∴第30天的日销售利润最大,最大利润为2 450元;
(2)由(1)得:当1≤t≤40时,
w=﹣(t﹣30)2+2450,
令w=2400,即﹣(t﹣30)2+2450=2400,
解得:t1=20,t2=40,
由函数w=﹣(t﹣30)2+2450图象可知,
当20≤t≤40时,日销售利润不低于2400元,
而当41≤t≤80时,w最大=2301<2400,
∴t的取值范围是20≤t≤40,
∴共有21天符合条件;
(3)设日销售利润为w,根据题意,得:
w=(t+16﹣6﹣m)(﹣2t+200)
=﹣t2+(30+2m)t+2000﹣200m,
由题意知,前40天,w随t的增大而增大,
﹣×392+39(30+2m)+2000﹣200m<﹣×402+40(30+2m)+200﹣200m,
解得:m>,
又m<7,
∴<m<7.
同课章节目录
