苏教版 四年级数学下册-多边形的内角和 课件(共27张PPT)
文档属性
| 名称 | 苏教版 四年级数学下册-多边形的内角和 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 10:04:21 | ||
图片预览





文档简介
(共27张PPT)
多边形的内角和
在2008年的北京奥运会上有很多设计美丽的多边形花坛。猜想:是否存在一个内角和为2008°的多边形花坛
你能从下列图片中找出你所熟悉的图形吗?
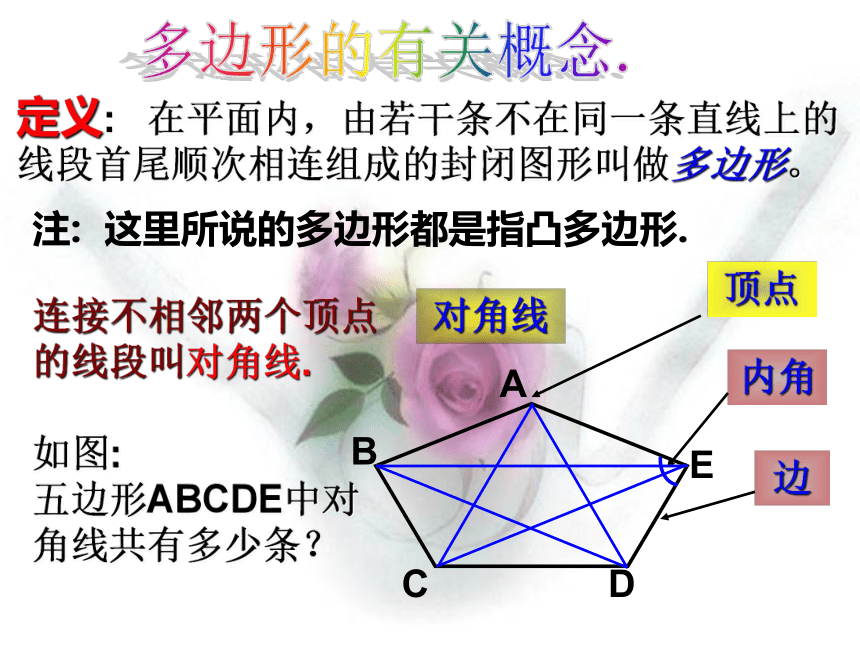
边
内角
顶点
定义: 在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
对角线
D
B
A
E
C
注: 这里所说的多边形都是指凸多边形.
连接不相邻两个顶点的线段叫对角线.
如图:
五边形ABCDE中对角线共有多少条?
多边形的有关概念.
n边形从一个顶点出发的 对角线把 n边形分成 个三角形, 条对角线.
n - 2
n - 3
上图广场中心的边缘是一个五边形,
我们将共同来探求它的五个内角的和.
1
2
3
4
5
探索五边形的内角和你有几种方法 请和同伴一起交流.
老师希望你有更多的方法和同学们一起分享
合作与探究
A
B
C
D
E
我们知道,三角形的内角和是 度,四边形的内角和是 度,那这个五边形的内角和呢?
小明利用右图求出了五边形的内角和,你知道他是怎么做的吗?
180
360
你能动手做一做吗
180°×3= 540°
想一想
E
A
B
C
D
.
O
小亮是利用下图求出五边形的内角和的,你知道他又是怎么做的吗?
你想到了吗
180°×5 - 360° = 540°
想一想
A
B
C
D
E
F
180°×4 -180° =540°
想一想
这个也不错哦
180°×4 -180° =540°
通过以上的学习,让我知道了解决问题方法的多样化,了解到数学中一种重要的解题思想叫做转化的思想.如求五边形的内角和可以通过分割转化为三角形问题来解决,对于其它的多边形也可以采用同样的方法。
我知道
多边形的边数 3 4 5 6 … n
分成的三角形个数 …
多边形的内角和 …
为了求得n边形的内角和,请根据下图所示,完成表格。
1
2
3
4
n-2
180°
540°
(n-2)×180°
你找到规律了吗?
360°
720°
我终于得到了本节课的结论啦
n边形的内角和等于(n-2)× 180°
(n≥3)
1.知道多边形的边数,可以说出多边形的度数。
2.知道多边形的度数,可以说出多边形的边数。
我能说
1、八边形的内角和等于多少度?十边形呢?
抢答
2、已知一个多边形,它的内角和 等于720°, 求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于 (n-2) 180°,
所以, (n-2) 180°= 720 。
解得: n=6
这个多边形的边数为6。
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形。
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。如正三角形、正四边形(正方形)、正五边形等等 。
正三角形
正四边形
正五边形
正六边形
正八边形
(或正三边形)
(或正四边形)
(1)一个多边形的边都相等,它的内角一定都相吗?
(2)一个多边形的内角都相等,它的边一定都相吗?
(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
(不一定,如菱形的边都相等,但内角不一定相等)
(不一定,如长方形的内角都相等,但边未必都相等)
60
90
120
108
135
议一议
正n边形的一个内角=
我发现
3、一个四边形的四个内角之比为7:8:2:1,则这四个角的大小分别为 °、 °、 °、 °
4、如右图示,四边形ABCD中,
AB⊥BC,AD ⊥CD,若∠C= 64°,那么∠A= °.
A
B
D
C
看看谁又对又快
考考你,能行吗?
1、___ 边形内角和是四边形内角和的2倍。
2、一个多边形的边数增加1,则内角和增加的度数 是 .
3、已知多边形内角和等于1080 ,求它的边数。
4、已知多边形每个内角都等于150°,求它的
边数及内角和.
5、过某个多边形一个顶点的所有对角线,将这个
多边形分成5个三角形。这个多边形是几边形?它
的内角和是多少?
课后思考
1、在2008年的北京奥运会上有很多设计美丽的多边形花坛,猜想:是否存在一个内角和为2008°的多边形花坛?
2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定
有一张长方形桌面,它的四个内角和是360°,现在锯掉它的一个内角,你认为有几种锯法?每种锯法剩下的残余桌面所有的内角和是多少度?
讨论实践
1、多边形的定义和正多边形的定义。
2、多边形的内角和定理。
3、知道了多边形内角和的多种求解方法。
4、能利用多边形的内角和定理进行相关的 计算。
5、在探求过程中我们使用了观察、归纳的数学方法,并且运用了类比、转化等数学思想。
今天你有什么收获?
谢 谢!
多边形的内角和
在2008年的北京奥运会上有很多设计美丽的多边形花坛。猜想:是否存在一个内角和为2008°的多边形花坛
你能从下列图片中找出你所熟悉的图形吗?
边
内角
顶点
定义: 在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
对角线
D
B
A
E
C
注: 这里所说的多边形都是指凸多边形.
连接不相邻两个顶点的线段叫对角线.
如图:
五边形ABCDE中对角线共有多少条?
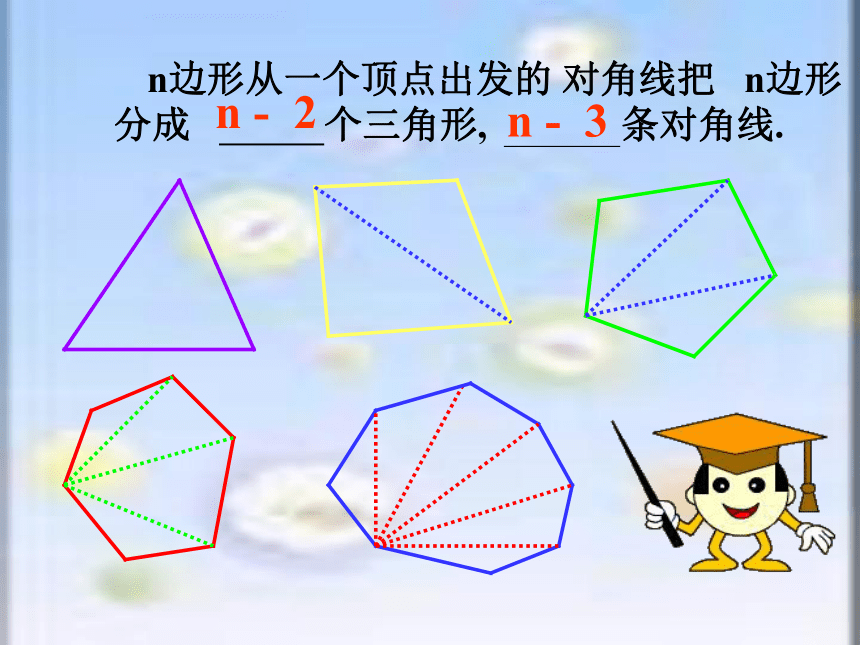
多边形的有关概念.
n边形从一个顶点出发的 对角线把 n边形分成 个三角形, 条对角线.
n - 2
n - 3
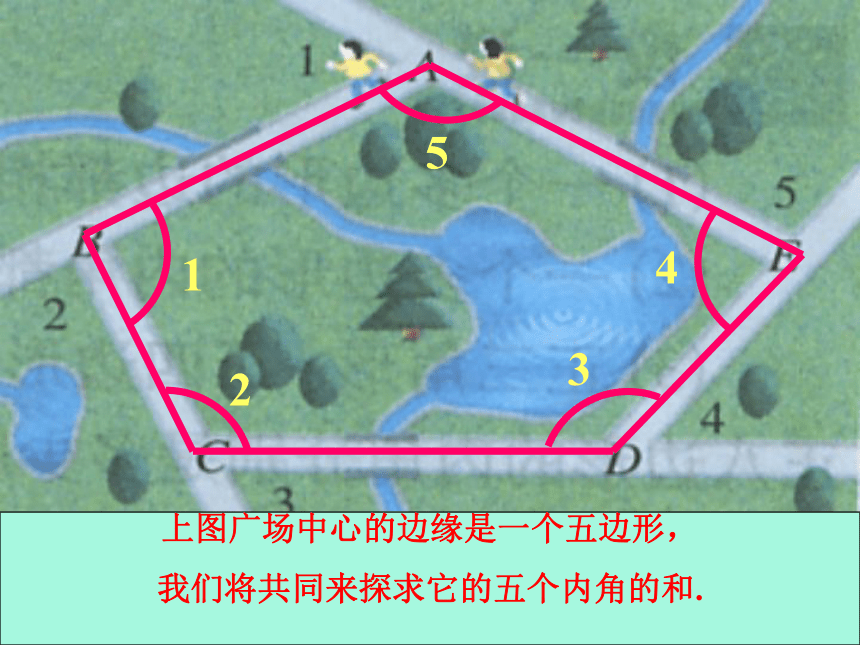
上图广场中心的边缘是一个五边形,
我们将共同来探求它的五个内角的和.
1
2
3
4
5
探索五边形的内角和你有几种方法 请和同伴一起交流.
老师希望你有更多的方法和同学们一起分享
合作与探究
A
B
C
D
E
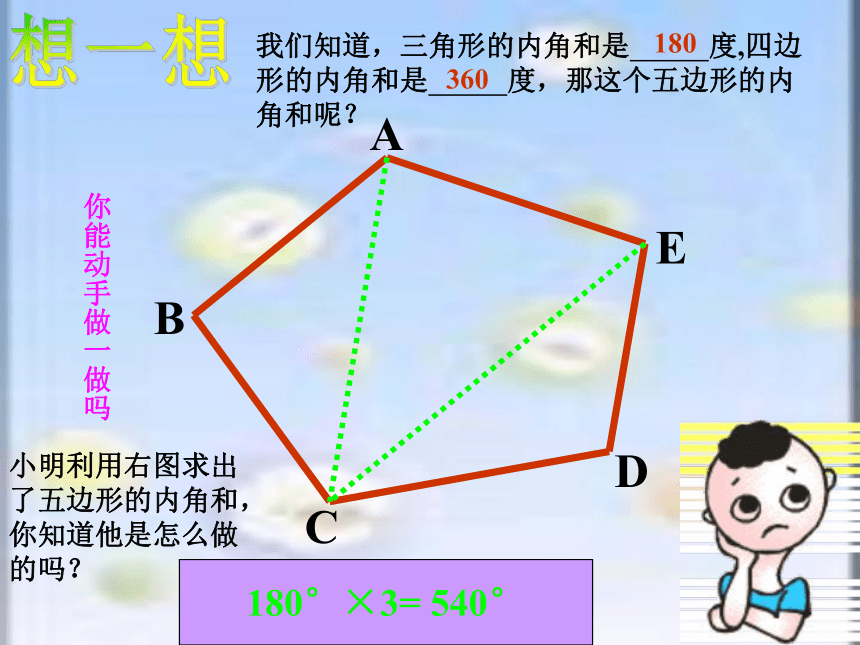
我们知道,三角形的内角和是 度,四边形的内角和是 度,那这个五边形的内角和呢?
小明利用右图求出了五边形的内角和,你知道他是怎么做的吗?
180
360
你能动手做一做吗
180°×3= 540°
想一想
E
A
B
C
D
.
O
小亮是利用下图求出五边形的内角和的,你知道他又是怎么做的吗?
你想到了吗
180°×5 - 360° = 540°
想一想
A
B
C
D
E
F
180°×4 -180° =540°
想一想
这个也不错哦
180°×4 -180° =540°
通过以上的学习,让我知道了解决问题方法的多样化,了解到数学中一种重要的解题思想叫做转化的思想.如求五边形的内角和可以通过分割转化为三角形问题来解决,对于其它的多边形也可以采用同样的方法。
我知道
多边形的边数 3 4 5 6 … n
分成的三角形个数 …
多边形的内角和 …
为了求得n边形的内角和,请根据下图所示,完成表格。
1
2
3
4
n-2
180°
540°
(n-2)×180°
你找到规律了吗?
360°
720°
我终于得到了本节课的结论啦
n边形的内角和等于(n-2)× 180°
(n≥3)
1.知道多边形的边数,可以说出多边形的度数。
2.知道多边形的度数,可以说出多边形的边数。
我能说
1、八边形的内角和等于多少度?十边形呢?
抢答
2、已知一个多边形,它的内角和 等于720°, 求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于 (n-2) 180°,
所以, (n-2) 180°= 720 。
解得: n=6
这个多边形的边数为6。
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形。
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。如正三角形、正四边形(正方形)、正五边形等等 。
正三角形
正四边形
正五边形
正六边形
正八边形
(或正三边形)
(或正四边形)
(1)一个多边形的边都相等,它的内角一定都相吗?
(2)一个多边形的内角都相等,它的边一定都相吗?
(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
(不一定,如菱形的边都相等,但内角不一定相等)
(不一定,如长方形的内角都相等,但边未必都相等)
60
90
120
108
135
议一议
正n边形的一个内角=
我发现
3、一个四边形的四个内角之比为7:8:2:1,则这四个角的大小分别为 °、 °、 °、 °
4、如右图示,四边形ABCD中,
AB⊥BC,AD ⊥CD,若∠C= 64°,那么∠A= °.
A
B
D
C
看看谁又对又快
考考你,能行吗?
1、___ 边形内角和是四边形内角和的2倍。
2、一个多边形的边数增加1,则内角和增加的度数 是 .
3、已知多边形内角和等于1080 ,求它的边数。
4、已知多边形每个内角都等于150°,求它的
边数及内角和.
5、过某个多边形一个顶点的所有对角线,将这个
多边形分成5个三角形。这个多边形是几边形?它
的内角和是多少?
课后思考
1、在2008年的北京奥运会上有很多设计美丽的多边形花坛,猜想:是否存在一个内角和为2008°的多边形花坛?
2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定
有一张长方形桌面,它的四个内角和是360°,现在锯掉它的一个内角,你认为有几种锯法?每种锯法剩下的残余桌面所有的内角和是多少度?
讨论实践
1、多边形的定义和正多边形的定义。
2、多边形的内角和定理。
3、知道了多边形内角和的多种求解方法。
4、能利用多边形的内角和定理进行相关的 计算。
5、在探求过程中我们使用了观察、归纳的数学方法,并且运用了类比、转化等数学思想。
今天你有什么收获?
谢 谢!
