2021-2022学年苏科版九年级数学上册第2章对称图形圆--2.8圆锥的侧面积简单练习(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册第2章对称图形圆--2.8圆锥的侧面积简单练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 08:18:59 | ||
图片预览




文档简介
2.8圆锥的侧面积简单练习
一、选择题
若 的半径为 ,点 到圆心 的距离为 ,则点 与 的位置关系是
A.点 在圆内 B.点 在圆上 C.点 在圆外 D.不能确定
已知圆锥的母线长为 ,底面半径为 ,则圆锥的表面积为
A. B. C. D.
如果圆锥的母线长为 ,底面圆的半径为 ,则这个圆锥的侧面积为
A. B. C. D.
圆锥的底面半径为 ,母线长为 ,它的侧面积为
A. B. C. D.
如图,已知在 中,,,,若把 绕直线 旋转一周,则所得圆锥的侧面积等于
A. B. C. D.
下列说法中,错误的是
A.等弧所对的圆周角相等
B.同弧所对的圆周角相等
C.在同圆或等圆中,相等的圆周角所对的弧相等
D.同圆中,等弦所对的圆周角相等
一个圆锥的底面半径为 ,母线长为 ,其侧面积是
A. B. C. D.
如图,已知一块圆心角为 的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是 ,则这块扇形铁皮的半径是
A. B. C. D.
已知圆锥的底面半径为 ,母线长为 ,则圆锥的侧面积是
A. B. C. D.
若一个圆锥的侧面展开图是半径为 ,圆心角为 的扇形,则这个圆锥的底面半径长是
A. B. C. D.
二、填空题
如图,圆锥的底面直径是 ,高为 ,则它的侧面展开图的面积是 .
已知圆锥的底面圆半径为 ,其母线长为 ,则圆锥的侧面积等于 .
等底等高的圆柱与圆锥,已知圆柱的体积是 立方厘米,则圆锥的体积是 立方厘米.
已知圆锥的底面圆半径是 ,母线长是 ,则圆锥侧面展开的扇形圆心角是 .
用一个圆心角为 ,半径为 的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .
如图,在一张正方形纸片上剪下一个半径为 的圆形和一个半径为 的扇形,使之恰好围成图中所示的圆锥,则 与 之间的关系是 .
著名画家达 芬奇不仅画艺超群,同时还是一个数学家、发明家,他曾经设计过一种如图所示的圆规,有两个互相垂直的滑槽(滑槽的宽度忽略不计),一根没有弹性的木棒两端 , 能在滑槽内自由滑动,将笔插入位于木棒中点 处的小孔中,随着木棒的滑动就可以画出一个圆,若 ,则画出的圆的半径为 .
一个圆锥的侧面展开图是半径为 的半圆,则这个圆锥的底面半径为 .
三、解答题
如图,有一直径是 米的圆形铁皮,要从中剪出一个圆心角是 的扇形 .求:
(1) 被剪掉阴影部分的面积;
(2) 若用所留的扇形铁皮围成一个圆锥,该圆锥底面圆的半径是多少米?
在城市规划建设中,某超市需要拆迁.爆破时,导火索的燃烧速度为每秒 ,点导火索的人需在爆破前跑到离爆破点 以外的安全区域.这个导火索的长度为 ,那么点导火索的人以 的速度往外跑是否安全?
如图, 是 平分线上的一点,以 为圆心的圆和 的两边分别交于点 , 和点 ,.求证:.
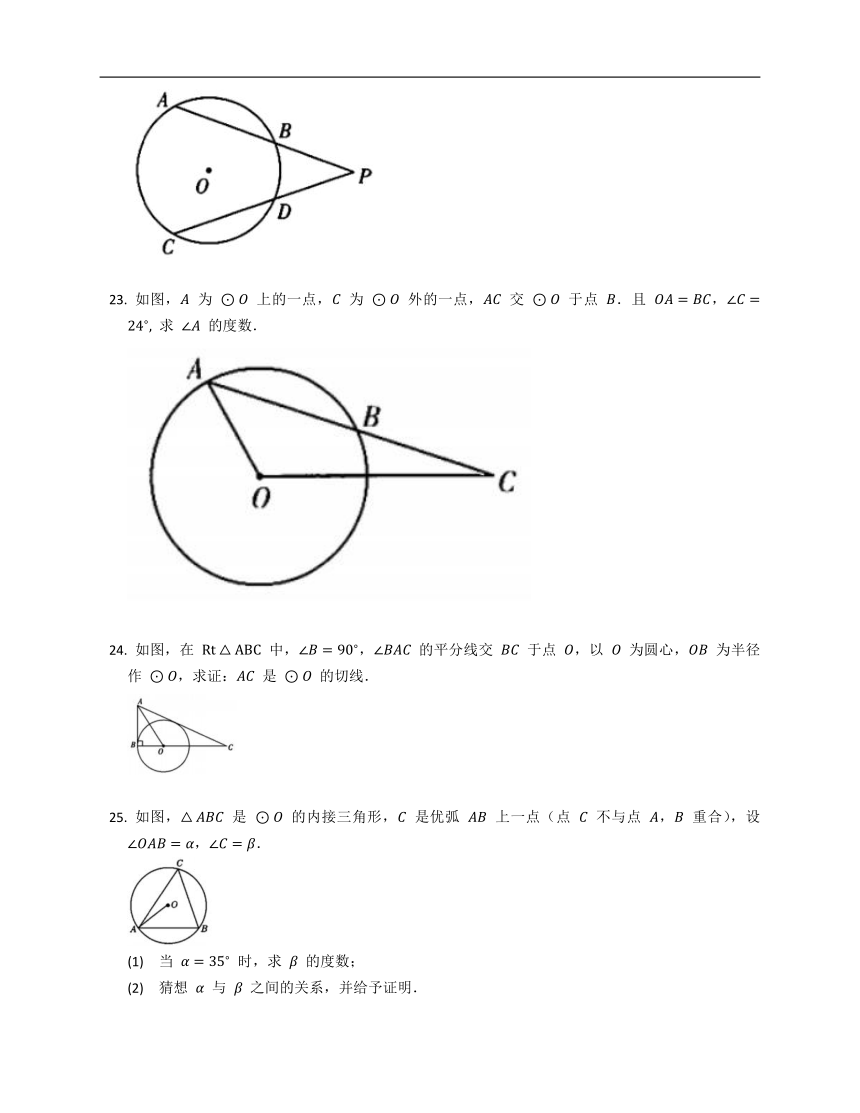
如图, 的弦 , 的延长线相交于点 ,且 .求证:.
如图, 为 上的一点, 为 外的一点, 交 于点 .且 , 求 的度数.
如图,在 中,, 的平分线交 于点 ,以 为圆心, 为半径作 ,求证: 是 的切线.
如图, 是 的内接三角形, 是优弧 上一点(点 不与点 , 重合),设 ,.
(1) 当 时,求 的度数;
(2) 猜想 与 之间的关系,并给予证明.
如图,用圆心角为 ,半径为 的扇形纸片卷成一个圆锥形无底纸帽.
(1) 求这个纸帽的底面周长;
(2) 求这个纸帽的底面半径;
(3) 求这个纸帽的侧面积.
如图,在平面直角坐标系 中,以点 为圆心的 交 轴于点 ,,,求 的半径.
如图,在平面直角坐标系中, 的半径为 ,则直线 与 的位置关系怎样?
答案
一、选择题(共10题)
1. 【答案】A
【知识点】通过r与d判断点与圆的位置关系
2. 【答案】B
【知识点】圆锥的计算
3. 【答案】B
【解析】底面圆半径为 ,,.
故选B.
【知识点】圆锥的计算
4. 【答案】B
【解析】根据圆锥的底面半径为 ,母线长为 ,直接利用圆锥的侧面积公式求出它的侧面积.根据圆锥的侧面积公式:.
故答案选:B.
【知识点】圆锥的计算
5. 【答案】D
【解析】 ,
底面的周长是:,
圆锥的侧面积等 .
【知识点】圆锥的计算
6. 【答案】D
【知识点】弧、弦、圆心角的关系定理
7. 【答案】C
【知识点】圆锥的计算
8. 【答案】A
【解析】 圆锥的底面直径为 ,
圆锥的底面周长为 ,
扇形的弧长为 ,
设扇形的半径为 ,则 ,
解得:.
【知识点】圆锥的计算
9. 【答案】C
【解析】圆锥的侧面积 .
【知识点】圆锥的计算
10. 【答案】C
【解析】设这个圆锥的底面半径为 ,
根据题意得 ,
解得 ,
所以这个圆锥的底面半径长为 .
【知识点】圆锥的计算
二、填空题(共8题)
11. 【答案】
【解析】 圆锥的底面直径是 ,高为 ,
由勾股定理得圆锥的母线长为 ,
圆锥的侧面积为 .
【知识点】圆锥的展开图、圆锥的计算
12. 【答案】
【解析】圆锥的侧面积公式为 ,故侧面积为 .
【知识点】圆锥的计算
13. 【答案】
【解析】 (立方厘米).
【知识点】圆锥的计算
14. 【答案】
【解析】 圆锥的底面圆半径是 ,
底面圆周长为 .
又圆锥的母线长是 ,
圆锥侧面展开的扇形圆心角是 .
【知识点】圆锥的计算
15. 【答案】
【解析】设圆锥底面的半径为 ,
扇形的弧长为:,
圆锥的底面周长等于它的侧面展开图的弧长,
根据题意得 ,
解得:.
【知识点】圆锥的计算
16. 【答案】
【解析】试题根据题意可得:扇形的弧长是:,圆的半径为 ,则底面圆的周长是 ,
所以 ,所以 .
【知识点】圆锥的计算、解析式法
17. 【答案】
【知识点】直角三角形斜边的中线
18. 【答案】
【解析】设这个圆锥的底面半径为 ,
根据题意得 ,解得 .
【知识点】圆锥的计算
三、解答题(共10题)
19. 【答案】
(1) 连接 ,,,
,,
.
又 ,
,
是等边三角形,
米,
(平方米),
(平方米).
(2) 在扇形 中, 的长为 (米).
设底面圆的半径为 米,则 ,
,
该圆锥底面圆的半径是 米.
【知识点】扇形面积的计算、图形初步、圆锥的表面积计算
20. 【答案】导火索燃烧的时间为 ,
点导火索的人跑 所用的时间为 ,
因为 ,所以安全.
【知识点】圆的相关元素
21. 【答案】作 于点 , 于点 .
由角平分线上的点到角的两边距离相等,得 .
又 ,
.
.
【知识点】圆的相关元素
22. 【答案】连接 ,
因为 ,
所以 .
所以 ,即 .
所以 .
所以 .
【知识点】弧、弦、圆心角的关系定理
23. 【答案】连接 ,
,,
,,
,
,
.
【知识点】圆的相关元素
24. 【答案】如图,过点 作 ,垂足为 .
平分 ,,
,
即点 到 的距离等于 的半径,
是 的切线.
【知识点】切线的判定
25. 【答案】
(1) 如答图,连接 .
,
,
,
.
(2) 与 的关系为 .
证明:
,
,
,
.
【知识点】圆周角定理及其推理、三角形的内角和、等腰三角形的性质
26. 【答案】
(1) 由题意,得扇形弧长为 .
易得这个纸帽的底面周长与扇形的弧长相等,
这个纸帽的底面周长为 .
(2) 设这个纸帽的底面半径是 ,
由()得纸帽的底面周长为 ,
,
解得 ,
这个纸帽的底面半径是 .
(3) 易得这个纸帽的侧面积等于扇形的面积,
扇形的面积为 ,
这个纸帽的侧面积为 .
【知识点】圆锥的计算
27. 【答案】如图,过点 作 于点 ,连接 ,
则 .
点 的坐标是 ,
,
在 中,,
的半径为 .
【知识点】垂径定理
28. 【答案】如图,过点 作 直线 ,垂足为 ,
直线 的解析式为 ,令 ,解得 ,
令 ,解得 ,
,,即 ,,
在 中,根据勾股定理得 ,
又 ,
,
又 的半径为 ,
则直线 与 的位置关系是相切.
【知识点】一次函数的解析式、切线的判定、一次函数的图象与性质
一、选择题
若 的半径为 ,点 到圆心 的距离为 ,则点 与 的位置关系是
A.点 在圆内 B.点 在圆上 C.点 在圆外 D.不能确定
已知圆锥的母线长为 ,底面半径为 ,则圆锥的表面积为
A. B. C. D.
如果圆锥的母线长为 ,底面圆的半径为 ,则这个圆锥的侧面积为
A. B. C. D.
圆锥的底面半径为 ,母线长为 ,它的侧面积为
A. B. C. D.
如图,已知在 中,,,,若把 绕直线 旋转一周,则所得圆锥的侧面积等于
A. B. C. D.
下列说法中,错误的是
A.等弧所对的圆周角相等
B.同弧所对的圆周角相等
C.在同圆或等圆中,相等的圆周角所对的弧相等
D.同圆中,等弦所对的圆周角相等
一个圆锥的底面半径为 ,母线长为 ,其侧面积是
A. B. C. D.
如图,已知一块圆心角为 的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是 ,则这块扇形铁皮的半径是
A. B. C. D.
已知圆锥的底面半径为 ,母线长为 ,则圆锥的侧面积是
A. B. C. D.
若一个圆锥的侧面展开图是半径为 ,圆心角为 的扇形,则这个圆锥的底面半径长是
A. B. C. D.
二、填空题
如图,圆锥的底面直径是 ,高为 ,则它的侧面展开图的面积是 .
已知圆锥的底面圆半径为 ,其母线长为 ,则圆锥的侧面积等于 .
等底等高的圆柱与圆锥,已知圆柱的体积是 立方厘米,则圆锥的体积是 立方厘米.
已知圆锥的底面圆半径是 ,母线长是 ,则圆锥侧面展开的扇形圆心角是 .
用一个圆心角为 ,半径为 的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .
如图,在一张正方形纸片上剪下一个半径为 的圆形和一个半径为 的扇形,使之恰好围成图中所示的圆锥,则 与 之间的关系是 .
著名画家达 芬奇不仅画艺超群,同时还是一个数学家、发明家,他曾经设计过一种如图所示的圆规,有两个互相垂直的滑槽(滑槽的宽度忽略不计),一根没有弹性的木棒两端 , 能在滑槽内自由滑动,将笔插入位于木棒中点 处的小孔中,随着木棒的滑动就可以画出一个圆,若 ,则画出的圆的半径为 .
一个圆锥的侧面展开图是半径为 的半圆,则这个圆锥的底面半径为 .
三、解答题
如图,有一直径是 米的圆形铁皮,要从中剪出一个圆心角是 的扇形 .求:
(1) 被剪掉阴影部分的面积;
(2) 若用所留的扇形铁皮围成一个圆锥,该圆锥底面圆的半径是多少米?
在城市规划建设中,某超市需要拆迁.爆破时,导火索的燃烧速度为每秒 ,点导火索的人需在爆破前跑到离爆破点 以外的安全区域.这个导火索的长度为 ,那么点导火索的人以 的速度往外跑是否安全?
如图, 是 平分线上的一点,以 为圆心的圆和 的两边分别交于点 , 和点 ,.求证:.
如图, 的弦 , 的延长线相交于点 ,且 .求证:.
如图, 为 上的一点, 为 外的一点, 交 于点 .且 , 求 的度数.
如图,在 中,, 的平分线交 于点 ,以 为圆心, 为半径作 ,求证: 是 的切线.
如图, 是 的内接三角形, 是优弧 上一点(点 不与点 , 重合),设 ,.
(1) 当 时,求 的度数;
(2) 猜想 与 之间的关系,并给予证明.
如图,用圆心角为 ,半径为 的扇形纸片卷成一个圆锥形无底纸帽.
(1) 求这个纸帽的底面周长;
(2) 求这个纸帽的底面半径;
(3) 求这个纸帽的侧面积.
如图,在平面直角坐标系 中,以点 为圆心的 交 轴于点 ,,,求 的半径.
如图,在平面直角坐标系中, 的半径为 ,则直线 与 的位置关系怎样?
答案
一、选择题(共10题)
1. 【答案】A
【知识点】通过r与d判断点与圆的位置关系
2. 【答案】B
【知识点】圆锥的计算
3. 【答案】B
【解析】底面圆半径为 ,,.
故选B.
【知识点】圆锥的计算
4. 【答案】B
【解析】根据圆锥的底面半径为 ,母线长为 ,直接利用圆锥的侧面积公式求出它的侧面积.根据圆锥的侧面积公式:.
故答案选:B.
【知识点】圆锥的计算
5. 【答案】D
【解析】 ,
底面的周长是:,
圆锥的侧面积等 .
【知识点】圆锥的计算
6. 【答案】D
【知识点】弧、弦、圆心角的关系定理
7. 【答案】C
【知识点】圆锥的计算
8. 【答案】A
【解析】 圆锥的底面直径为 ,
圆锥的底面周长为 ,
扇形的弧长为 ,
设扇形的半径为 ,则 ,
解得:.
【知识点】圆锥的计算
9. 【答案】C
【解析】圆锥的侧面积 .
【知识点】圆锥的计算
10. 【答案】C
【解析】设这个圆锥的底面半径为 ,
根据题意得 ,
解得 ,
所以这个圆锥的底面半径长为 .
【知识点】圆锥的计算
二、填空题(共8题)
11. 【答案】
【解析】 圆锥的底面直径是 ,高为 ,
由勾股定理得圆锥的母线长为 ,
圆锥的侧面积为 .
【知识点】圆锥的展开图、圆锥的计算
12. 【答案】
【解析】圆锥的侧面积公式为 ,故侧面积为 .
【知识点】圆锥的计算
13. 【答案】
【解析】 (立方厘米).
【知识点】圆锥的计算
14. 【答案】
【解析】 圆锥的底面圆半径是 ,
底面圆周长为 .
又圆锥的母线长是 ,
圆锥侧面展开的扇形圆心角是 .
【知识点】圆锥的计算
15. 【答案】
【解析】设圆锥底面的半径为 ,
扇形的弧长为:,
圆锥的底面周长等于它的侧面展开图的弧长,
根据题意得 ,
解得:.
【知识点】圆锥的计算
16. 【答案】
【解析】试题根据题意可得:扇形的弧长是:,圆的半径为 ,则底面圆的周长是 ,
所以 ,所以 .
【知识点】圆锥的计算、解析式法
17. 【答案】
【知识点】直角三角形斜边的中线
18. 【答案】
【解析】设这个圆锥的底面半径为 ,
根据题意得 ,解得 .
【知识点】圆锥的计算
三、解答题(共10题)
19. 【答案】
(1) 连接 ,,,
,,
.
又 ,
,
是等边三角形,
米,
(平方米),
(平方米).
(2) 在扇形 中, 的长为 (米).
设底面圆的半径为 米,则 ,
,
该圆锥底面圆的半径是 米.
【知识点】扇形面积的计算、图形初步、圆锥的表面积计算
20. 【答案】导火索燃烧的时间为 ,
点导火索的人跑 所用的时间为 ,
因为 ,所以安全.
【知识点】圆的相关元素
21. 【答案】作 于点 , 于点 .
由角平分线上的点到角的两边距离相等,得 .
又 ,
.
.
【知识点】圆的相关元素
22. 【答案】连接 ,
因为 ,
所以 .
所以 ,即 .
所以 .
所以 .
【知识点】弧、弦、圆心角的关系定理
23. 【答案】连接 ,
,,
,,
,
,
.
【知识点】圆的相关元素
24. 【答案】如图,过点 作 ,垂足为 .
平分 ,,
,
即点 到 的距离等于 的半径,
是 的切线.
【知识点】切线的判定
25. 【答案】
(1) 如答图,连接 .
,
,
,
.
(2) 与 的关系为 .
证明:
,
,
,
.
【知识点】圆周角定理及其推理、三角形的内角和、等腰三角形的性质
26. 【答案】
(1) 由题意,得扇形弧长为 .
易得这个纸帽的底面周长与扇形的弧长相等,
这个纸帽的底面周长为 .
(2) 设这个纸帽的底面半径是 ,
由()得纸帽的底面周长为 ,
,
解得 ,
这个纸帽的底面半径是 .
(3) 易得这个纸帽的侧面积等于扇形的面积,
扇形的面积为 ,
这个纸帽的侧面积为 .
【知识点】圆锥的计算
27. 【答案】如图,过点 作 于点 ,连接 ,
则 .
点 的坐标是 ,
,
在 中,,
的半径为 .
【知识点】垂径定理
28. 【答案】如图,过点 作 直线 ,垂足为 ,
直线 的解析式为 ,令 ,解得 ,
令 ,解得 ,
,,即 ,,
在 中,根据勾股定理得 ,
又 ,
,
又 的半径为 ,
则直线 与 的位置关系是相切.
【知识点】一次函数的解析式、切线的判定、一次函数的图象与性质
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
