研究平抛运动的规律课件
图片预览










文档简介
(共35张PPT)
1.2 研究平抛运动的规律
课前自主学案
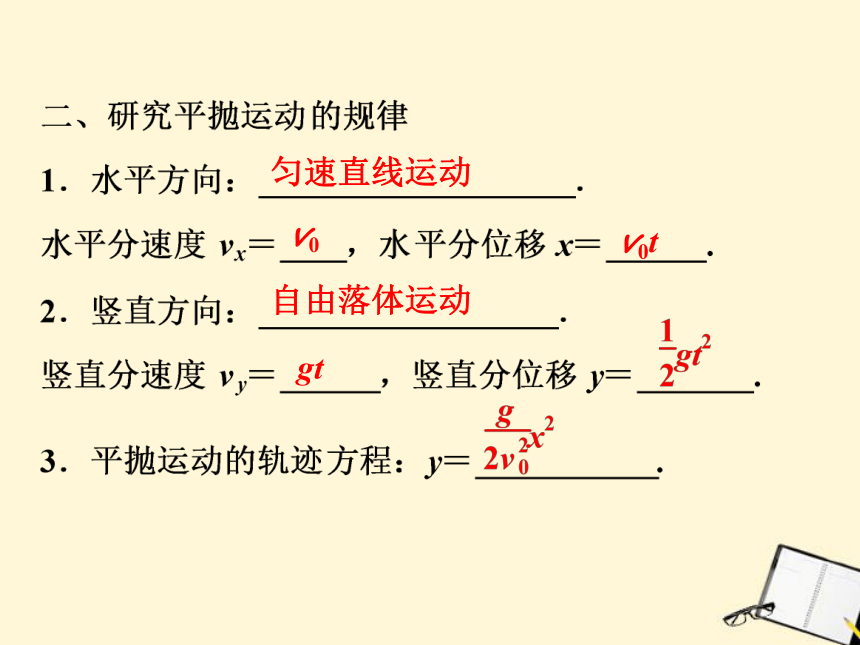
一、运动的合成与分解
1.合运动和分运动
(1)若物体的某一运动与另外两种运动的共同作用_________相同,则这一运动称为另外两种运动的__________,另外两种运动称为__________.
(2)由分运动求合运动叫___________,由合运动求分运动叫_______________.
效果
合运动
分运动
运动的合成
运动的分解
2.怎样求合运动或分运动
(1)合运动和分运动的三大特性:______、______、___________.
(2)运动的合成与分解遵循__________________.
3.运用平行四边形定则可以算出平抛运动物体的________、_________等物理量.
等时性
等效性
独立性
平行四边形定则
位移
速度
匀速直线运动
v0
v0t
自由落体运动
gt
核心要点突破
一、合运动与分运动的关系
1.合运动与分运动的性质
(1)等效性:各个分运动共同产生的效果与合运动的效果相同.
(2)等时性:各个分运动经历的时间与合运动的时间相等.
(3)独立性:各分运动独立进行不受其他分运动的影响.
(4)同一性:各分运动与合运动必须对应同一物体的运动.
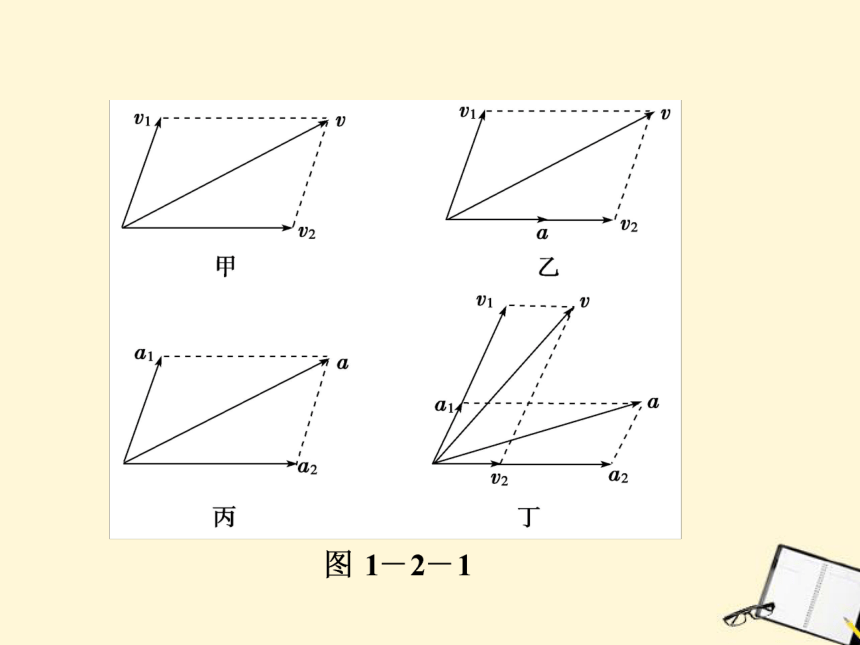
(4)两个初速度不为零的匀加速直线运动,其初速度v1和v2的矢量和为v,加速度a1和a2的矢量和为a;若v和a在一条直线上,则物体做匀变速直线运动,若v和a不在一条直线上,则物体做匀变速曲线运动.(如图1-2-1丁)
3.如何确定一个运动的分运动
求某一个运动的分运动叫做运动的分解,是运动合成的逆运算,如何确定一个运动的分运动呢?一般应按下列步骤:
(1)根据运动的效果(产生位移)确定运动分解方向;
(2)应用平行四边形定则,画出运动分解图;
(3)将平行四边形转化为三角形,应用数学知识求解.
即时应用 (即时突破,小试牛刀)
1.关于运动的合成,下列说法中正确的是 ( )
A.两个直线运动的合运动,一定是直线运动
B.两个直线运动的合运动,可能是曲线运动
C.两个互成角度的匀速直线运动的合运动,一定是匀速直线运动
D.两个互成角度的匀加速直线运动的合运动,一定是匀加速直线运动.
解析:选BC.两个匀速运动的合成,就是其速度的合成,其合速度的方向是确定的,等于两个分速度的矢量和,加速度为零,即合力为零,故合运动一定是匀速直线运动,C对;两个分运动的合加速度方向与合速度的方向,不一定在同一直线上,既有可能做曲线运动,也可能做直线运动,不是“一定”,而是“可能”,故A、D错,B对.
即时应用 (即时突破,小试牛刀)
2.游泳运动员以恒定的速率垂直河岸横渡,当水速突然增大时,对运动员横渡经历的路程、时间发生的影响是( )
A.路程增加、时间增加
B.路程增加、时间缩短
C.路程、时间均与水速无关
D.路程增加、时间不变
图1-2-5
(4)在平抛物体的运动中,任意两个时刻的速度变化量Δv=g·Δt,方向恒为竖直向下,其v0、Δv、vt三个速度矢量构成的三角形一定是直角三角形.如图1-2-5所示.
即时应用 (即时突破,小试牛刀)
3.(2011年高考广东理综卷)如图1-2-7所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知底线到网的距离为L,重力加速度取g,将球的运动视作平抛运动,下列叙述正确的是( )
图1-2-9
【答案】 5 D
【方法总结】 合运动是物体(质点)的实际运动,而分运动是物体(质点)同时参与的几个运动.在处理问题时,选择的参考系必须是同一个参考系.在实际生活中经常要把一个物体的速度进行分解来解决问题,分解时应按实际效果进行分解,否则分速度就毫无意义.
分解绳(或杆)连接的物体的速度.
例2
通过解决下列问题,体会运动的效果和力的效果的不同.如图1-2-10所示,轻绳通过定滑轮拉动物体,使其在水平面上运动.若拉绳的速度为v0,当绳与水平方向夹角为θ时,物体的速度v为________.若此时绳上的拉力大小为F,物体的质量为m,忽略地面的摩擦力,那么,此时物体的加速度为________.
图1-2-10
【方法总结】 (1)在进行速度分解时,首先要分清合速度与分速度(合速度就是物体实际运动的速度);其次根据效果相同,由物体的实际运动确定其是由哪些分运动叠加的,从而找出相应的分速度的方向;然后根据平行四边形定则画出合速度与分速度的关系图,由几何知识得到它们的关系.
(2)由于绳(或杆)不可伸缩,所以用绳(或杆)连接的物体沿绳(或杆)方向上的速度大小相等.
如图1-2-12所示,从倾角为θ的斜面上的A点,以水平速度v0抛出一个小球,不计空气阻力,它落在斜面上B点所用的时间为( )
平抛斜面类问题
例3
图1-2-12
图1-2-13
【答案】 B
1.2 研究平抛运动的规律
课前自主学案
一、运动的合成与分解
1.合运动和分运动
(1)若物体的某一运动与另外两种运动的共同作用_________相同,则这一运动称为另外两种运动的__________,另外两种运动称为__________.
(2)由分运动求合运动叫___________,由合运动求分运动叫_______________.
效果
合运动
分运动
运动的合成
运动的分解
2.怎样求合运动或分运动
(1)合运动和分运动的三大特性:______、______、___________.
(2)运动的合成与分解遵循__________________.
3.运用平行四边形定则可以算出平抛运动物体的________、_________等物理量.
等时性
等效性
独立性
平行四边形定则
位移
速度
匀速直线运动
v0
v0t
自由落体运动
gt
核心要点突破
一、合运动与分运动的关系
1.合运动与分运动的性质
(1)等效性:各个分运动共同产生的效果与合运动的效果相同.
(2)等时性:各个分运动经历的时间与合运动的时间相等.
(3)独立性:各分运动独立进行不受其他分运动的影响.
(4)同一性:各分运动与合运动必须对应同一物体的运动.
(4)两个初速度不为零的匀加速直线运动,其初速度v1和v2的矢量和为v,加速度a1和a2的矢量和为a;若v和a在一条直线上,则物体做匀变速直线运动,若v和a不在一条直线上,则物体做匀变速曲线运动.(如图1-2-1丁)
3.如何确定一个运动的分运动
求某一个运动的分运动叫做运动的分解,是运动合成的逆运算,如何确定一个运动的分运动呢?一般应按下列步骤:
(1)根据运动的效果(产生位移)确定运动分解方向;
(2)应用平行四边形定则,画出运动分解图;
(3)将平行四边形转化为三角形,应用数学知识求解.
即时应用 (即时突破,小试牛刀)
1.关于运动的合成,下列说法中正确的是 ( )
A.两个直线运动的合运动,一定是直线运动
B.两个直线运动的合运动,可能是曲线运动
C.两个互成角度的匀速直线运动的合运动,一定是匀速直线运动
D.两个互成角度的匀加速直线运动的合运动,一定是匀加速直线运动.
解析:选BC.两个匀速运动的合成,就是其速度的合成,其合速度的方向是确定的,等于两个分速度的矢量和,加速度为零,即合力为零,故合运动一定是匀速直线运动,C对;两个分运动的合加速度方向与合速度的方向,不一定在同一直线上,既有可能做曲线运动,也可能做直线运动,不是“一定”,而是“可能”,故A、D错,B对.
即时应用 (即时突破,小试牛刀)
2.游泳运动员以恒定的速率垂直河岸横渡,当水速突然增大时,对运动员横渡经历的路程、时间发生的影响是( )
A.路程增加、时间增加
B.路程增加、时间缩短
C.路程、时间均与水速无关
D.路程增加、时间不变
图1-2-5
(4)在平抛物体的运动中,任意两个时刻的速度变化量Δv=g·Δt,方向恒为竖直向下,其v0、Δv、vt三个速度矢量构成的三角形一定是直角三角形.如图1-2-5所示.
即时应用 (即时突破,小试牛刀)
3.(2011年高考广东理综卷)如图1-2-7所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上.已知底线到网的距离为L,重力加速度取g,将球的运动视作平抛运动,下列叙述正确的是( )
图1-2-9
【答案】 5 D
【方法总结】 合运动是物体(质点)的实际运动,而分运动是物体(质点)同时参与的几个运动.在处理问题时,选择的参考系必须是同一个参考系.在实际生活中经常要把一个物体的速度进行分解来解决问题,分解时应按实际效果进行分解,否则分速度就毫无意义.
分解绳(或杆)连接的物体的速度.
例2
通过解决下列问题,体会运动的效果和力的效果的不同.如图1-2-10所示,轻绳通过定滑轮拉动物体,使其在水平面上运动.若拉绳的速度为v0,当绳与水平方向夹角为θ时,物体的速度v为________.若此时绳上的拉力大小为F,物体的质量为m,忽略地面的摩擦力,那么,此时物体的加速度为________.
图1-2-10
【方法总结】 (1)在进行速度分解时,首先要分清合速度与分速度(合速度就是物体实际运动的速度);其次根据效果相同,由物体的实际运动确定其是由哪些分运动叠加的,从而找出相应的分速度的方向;然后根据平行四边形定则画出合速度与分速度的关系图,由几何知识得到它们的关系.
(2)由于绳(或杆)不可伸缩,所以用绳(或杆)连接的物体沿绳(或杆)方向上的速度大小相等.
如图1-2-12所示,从倾角为θ的斜面上的A点,以水平速度v0抛出一个小球,不计空气阻力,它落在斜面上B点所用的时间为( )
平抛斜面类问题
例3
图1-2-12
图1-2-13
【答案】 B
