北师大版八年级数学上册 5.5 应用二元一次方程组—里程碑上的数(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 5.5 应用二元一次方程组—里程碑上的数(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 09:59:38 | ||
图片预览








文档简介
(共23张PPT)
北师大版数学八年级上册第五章第五节
应用二元一次方程组——里程碑上的数
课前热身
1.一个两位数的十位数字是x,个位数字是y,则这个两位数可表示为: ;
2.一个三位数,若百位数字为a,十位数字为b,个位数字为c,则这个三位数为: ;
3.一个两位数,十位数字为a,个位数字为b,若在这两位数中间加一个0,得到一个三位数,则这个 三位数可表示为: ;
4.a为两位数,b是一个三位数,若把a放在b的左边得到一个五位数,则这个五位数可表示为: 。
10x+y
100a+10b+c
100a+b
1000a+b
情境导入
有一对父子,他们的年龄都
是一个两位数。下面是父子两人
对话:
爸爸说:“咱俩的年龄之和
才68岁,爸爸还是很年轻的!”
儿子说:“若把你的年龄写在我的年龄的左边,得到一
个四位数;若把你的年龄写在我的年龄的右边,同样得到
一个四位数。”
爸爸说:“如果这样的话,前一个四位数会比后一个四
位数大2178,这样看来爸爸已经很老了!”
聪明的同学们,听完他们的对话,你认为爸爸是年轻
还是很老呢?你能求出这对父子的年龄吗?
【解 析】
解:设爸爸年龄为 岁,儿子年龄为 岁,根据题意得:
整理得:
解方程组得:
答:爸爸的年龄为45岁,儿子的年龄为23岁。
学以致用
一个两位数,它的十位数字与个位数字的和为7.如果将这个两位数的十位数字与个位数字对调,那么所得的两位数比原两位数小27,求原来的两位数。
【解 析】
解:设原来两位数的十位数字为 ,个位数字为 ,根据
题意,得:
【小结】
关于数字问题的应用题,一般情况下要设间接未知数(设各个数位上的数字),用这些未知数表示相关数量,再根据等量关系列出方程(组)。
答:原来的两位数为52.
解得:
例题赏析
例1 甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4分钟后两人首次相遇此时乙还需要跑 300米才能跑完第一圈,求甲、乙二人的速度及环形场地的周长。
【解 析】
解:设乙的速度为 米/分,则甲的速度为2.5 米/分,环形
场地的周长为 米根据题意,得:
解得:
所以,
答:甲、乙二人的速度分别为375米/分,150米/分,
环形场地的周长为900米。
例题赏析
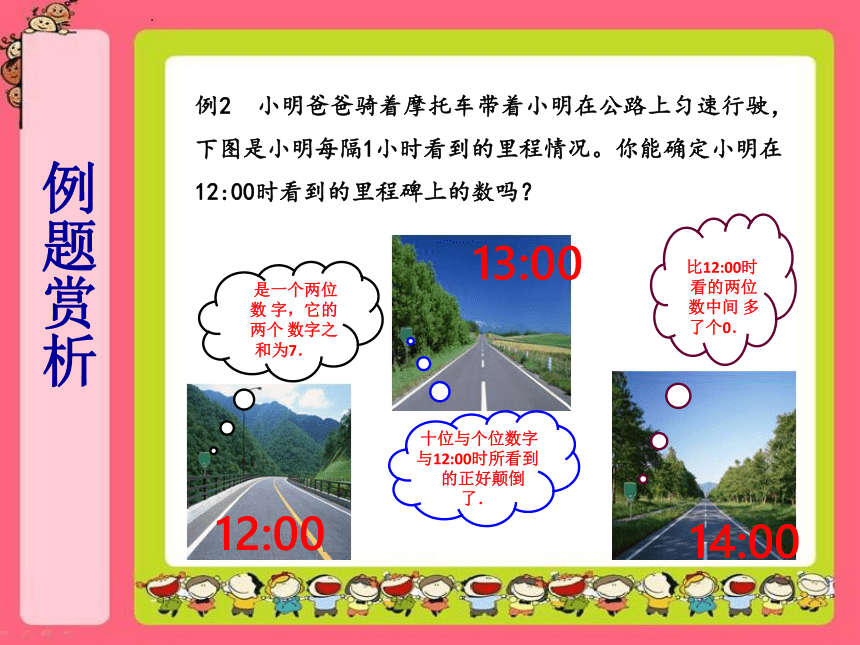
例2 小明爸爸骑着摩托车带着小明在公路上匀速行驶,
下图是小明每隔1小时看到的里程情况。你能确定小明在12:00时看到的里程碑上的数吗?
是一个两位
数 字,它的
两个 数字之和为7.
12:00
十位与个位数字 与12:00时所看到
的正好颠倒了.
13:00
比12:00时
看的两位
数中间 多了个0.
14:00
【解 析】
解:设小明在12:00看到的数十位数字是 ,个位数字是 ,
那么:
等量关系:
时 刻 百位数字 十位数字 个位数字 代数式
12:00
13:00
14:00
2)每隔一小时的路程差相等。
1)12:00看到的数的两个数字之和是7;
10x+y
10y+x
100x+y
x
x
x
y
y
y
0
【解 析】
解:设小明在12:00时看到的数的十位数字是 ,个位数字
是 ,根据题意,得:
【小结】
对较复杂的问题可以通过列表格的方法理清题中的
未知量,已知量以及等量关系,条理清楚。
整理,得: 解得:
答:小明在12:00时看到的里程碑上的数是16。
巩固提高
甲、乙两人分别从相距 30千米的 A,B两地同时相向而行,经过3小时后相距3千米,再经过2小时,甲到 B地所剩的路程是乙到A地所剩路程的2倍,你能求出甲、乙两人的速度吗?
(温馨提示:仔细审题,小心陷阱!!!)
【解 析】
解:设甲的速度为为 千米/时,乙的速度为 千米/时。
(1)当两人相遇之前相距3千米时,根据题意,得:
综上,甲的速度为 4千米/时,乙的速度为 5千米/时;
或甲的速度为 千米/时,乙的速度为 千米/时。
解得:
(2)当两人相遇之后相距3千米时,根据题意,得:
解得:
能力升华
请以小组为单位开展讨论,根据实际背景编一道应用题,使得其中的未知数满足方程组:
试试看。
比比谁做得更好!
你愿意当一次编题小老师吗?
课堂小结
1.关于数字问题的应用题,一般情况下要设间接未知数(设各个数位上的数字),用这些未知数表示相关数量,再根据等量关系列出方程(组)。
2.对较复杂的问题可以通过列表格的方法理清题中的未知量,已知量以及等量关系,条理清楚。
课堂小结
①审清题意;
②找出等量关系;
③设未知数x,y;
④列出二元一次方程组;
⑤解方程组;
⑥检验;
⑦作答。
3.用二元一次方程组解决实际问题的一般步骤:
课后作业
A组题:
1)小亮和小明做加法游戏,小明在第
一个加数的后面多写一个0,所得和
是242;小亮在另一个加数的后面多
写一个0,所得和是341,求原来的
两个加数分别是多少
2)甲、乙两人相距42km,如果两人从两地相向而行,2小时
后相遇,如果二人同时从两地出发,同向而行,14小时后
乙追上甲,求二人的速度。
3)汽车在上坡时速度为28km/h,下坡时速度42km/h,从甲地
到乙地用了4小时30分,返回时用了4小时40分,从甲地到
乙地上、下坡路各是多少千米?(列方程组不求解)
课后作业
B组题:
1)一个两位数,减去它的各位数字之和的3倍,结果是23;
这个两位数除以它的各位数字之和,商是5,余数是1.
这个两位数是多少?
2)A、B两地相距36千米,甲从A地步行到B地,乙从B地步行
到A地,两人同时相向出发,4小时后两人相遇,6小时
后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?
3)儿子问父亲今年多大,父亲笑着对儿子说:“我像你这
么大时,你才1岁;当你像我这么大时,我已经 67岁
了!”你知道父子俩今年各多少岁吗?你有几种解决问
题的方法?
课后作业
A组题解析:
1)解:设第一个加数为x,另一个加数为y,则
解得:
答:原来的两个加数分别是21和32。
2)解:设甲速度为xkm/h,乙速度为ykm/h,则
解得:
答:甲、乙二人的速度分别是9km/h和12km/h。
课后作业
A组题解析:
3)解:设从甲地到乙地上坡路有x千米,下坡路有y千米,则
解得:
答:从甲地到乙地上、下坡路各是70千米和84千米。
B组题解析:
1)解:设这个两位数的十位数字为x,个位数字为y,则
解得:
答:这个两位数分别是 5和 6。
课后作业
B组题解析:
2)解:设甲速度为xkm/h,乙速度为ykm/h,则
解得:
答:甲、乙二人的速度分别是4km/h和5km/h。
3)解法一:设儿子今年x岁,父亲今年y岁,如图所示,则
解得:
答:父子俩今年分别是23岁和45岁。
课后作业
B组题解析:
3)解法二:如图所示,无论是哪一年,父子年龄差不变。
故年龄差=(67-1)÷3=22(岁)
所以,22+1=23(岁)………儿子
22+23=45(岁)………父亲
答:父子俩今年分别是23岁和45岁。
解法三:设父子的年龄差为x岁,则儿子今年(x+1)岁,
父亲今年(2x+1)岁,父亲x年后67岁,则
2x+1+x=67, x=22. ∴ x+1=23, 2x+1=45
答:父子俩今年分别是23岁和45岁。
谢谢大家的配合
北师大版数学八年级上册第五章第五节
应用二元一次方程组——里程碑上的数
课前热身
1.一个两位数的十位数字是x,个位数字是y,则这个两位数可表示为: ;
2.一个三位数,若百位数字为a,十位数字为b,个位数字为c,则这个三位数为: ;
3.一个两位数,十位数字为a,个位数字为b,若在这两位数中间加一个0,得到一个三位数,则这个 三位数可表示为: ;
4.a为两位数,b是一个三位数,若把a放在b的左边得到一个五位数,则这个五位数可表示为: 。
10x+y
100a+10b+c
100a+b
1000a+b
情境导入
有一对父子,他们的年龄都
是一个两位数。下面是父子两人
对话:
爸爸说:“咱俩的年龄之和
才68岁,爸爸还是很年轻的!”
儿子说:“若把你的年龄写在我的年龄的左边,得到一
个四位数;若把你的年龄写在我的年龄的右边,同样得到
一个四位数。”
爸爸说:“如果这样的话,前一个四位数会比后一个四
位数大2178,这样看来爸爸已经很老了!”
聪明的同学们,听完他们的对话,你认为爸爸是年轻
还是很老呢?你能求出这对父子的年龄吗?
【解 析】
解:设爸爸年龄为 岁,儿子年龄为 岁,根据题意得:
整理得:
解方程组得:
答:爸爸的年龄为45岁,儿子的年龄为23岁。
学以致用
一个两位数,它的十位数字与个位数字的和为7.如果将这个两位数的十位数字与个位数字对调,那么所得的两位数比原两位数小27,求原来的两位数。
【解 析】
解:设原来两位数的十位数字为 ,个位数字为 ,根据
题意,得:
【小结】
关于数字问题的应用题,一般情况下要设间接未知数(设各个数位上的数字),用这些未知数表示相关数量,再根据等量关系列出方程(组)。
答:原来的两位数为52.
解得:
例题赏析
例1 甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4分钟后两人首次相遇此时乙还需要跑 300米才能跑完第一圈,求甲、乙二人的速度及环形场地的周长。
【解 析】
解:设乙的速度为 米/分,则甲的速度为2.5 米/分,环形
场地的周长为 米根据题意,得:
解得:
所以,
答:甲、乙二人的速度分别为375米/分,150米/分,
环形场地的周长为900米。
例题赏析
例2 小明爸爸骑着摩托车带着小明在公路上匀速行驶,
下图是小明每隔1小时看到的里程情况。你能确定小明在12:00时看到的里程碑上的数吗?
是一个两位
数 字,它的
两个 数字之和为7.
12:00
十位与个位数字 与12:00时所看到
的正好颠倒了.
13:00
比12:00时
看的两位
数中间 多了个0.
14:00
【解 析】
解:设小明在12:00看到的数十位数字是 ,个位数字是 ,
那么:
等量关系:
时 刻 百位数字 十位数字 个位数字 代数式
12:00
13:00
14:00
2)每隔一小时的路程差相等。
1)12:00看到的数的两个数字之和是7;
10x+y
10y+x
100x+y
x
x
x
y
y
y
0
【解 析】
解:设小明在12:00时看到的数的十位数字是 ,个位数字
是 ,根据题意,得:
【小结】
对较复杂的问题可以通过列表格的方法理清题中的
未知量,已知量以及等量关系,条理清楚。
整理,得: 解得:
答:小明在12:00时看到的里程碑上的数是16。
巩固提高
甲、乙两人分别从相距 30千米的 A,B两地同时相向而行,经过3小时后相距3千米,再经过2小时,甲到 B地所剩的路程是乙到A地所剩路程的2倍,你能求出甲、乙两人的速度吗?
(温馨提示:仔细审题,小心陷阱!!!)
【解 析】
解:设甲的速度为为 千米/时,乙的速度为 千米/时。
(1)当两人相遇之前相距3千米时,根据题意,得:
综上,甲的速度为 4千米/时,乙的速度为 5千米/时;
或甲的速度为 千米/时,乙的速度为 千米/时。
解得:
(2)当两人相遇之后相距3千米时,根据题意,得:
解得:
能力升华
请以小组为单位开展讨论,根据实际背景编一道应用题,使得其中的未知数满足方程组:
试试看。
比比谁做得更好!
你愿意当一次编题小老师吗?
课堂小结
1.关于数字问题的应用题,一般情况下要设间接未知数(设各个数位上的数字),用这些未知数表示相关数量,再根据等量关系列出方程(组)。
2.对较复杂的问题可以通过列表格的方法理清题中的未知量,已知量以及等量关系,条理清楚。
课堂小结
①审清题意;
②找出等量关系;
③设未知数x,y;
④列出二元一次方程组;
⑤解方程组;
⑥检验;
⑦作答。
3.用二元一次方程组解决实际问题的一般步骤:
课后作业
A组题:
1)小亮和小明做加法游戏,小明在第
一个加数的后面多写一个0,所得和
是242;小亮在另一个加数的后面多
写一个0,所得和是341,求原来的
两个加数分别是多少
2)甲、乙两人相距42km,如果两人从两地相向而行,2小时
后相遇,如果二人同时从两地出发,同向而行,14小时后
乙追上甲,求二人的速度。
3)汽车在上坡时速度为28km/h,下坡时速度42km/h,从甲地
到乙地用了4小时30分,返回时用了4小时40分,从甲地到
乙地上、下坡路各是多少千米?(列方程组不求解)
课后作业
B组题:
1)一个两位数,减去它的各位数字之和的3倍,结果是23;
这个两位数除以它的各位数字之和,商是5,余数是1.
这个两位数是多少?
2)A、B两地相距36千米,甲从A地步行到B地,乙从B地步行
到A地,两人同时相向出发,4小时后两人相遇,6小时
后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?
3)儿子问父亲今年多大,父亲笑着对儿子说:“我像你这
么大时,你才1岁;当你像我这么大时,我已经 67岁
了!”你知道父子俩今年各多少岁吗?你有几种解决问
题的方法?
课后作业
A组题解析:
1)解:设第一个加数为x,另一个加数为y,则
解得:
答:原来的两个加数分别是21和32。
2)解:设甲速度为xkm/h,乙速度为ykm/h,则
解得:
答:甲、乙二人的速度分别是9km/h和12km/h。
课后作业
A组题解析:
3)解:设从甲地到乙地上坡路有x千米,下坡路有y千米,则
解得:
答:从甲地到乙地上、下坡路各是70千米和84千米。
B组题解析:
1)解:设这个两位数的十位数字为x,个位数字为y,则
解得:
答:这个两位数分别是 5和 6。
课后作业
B组题解析:
2)解:设甲速度为xkm/h,乙速度为ykm/h,则
解得:
答:甲、乙二人的速度分别是4km/h和5km/h。
3)解法一:设儿子今年x岁,父亲今年y岁,如图所示,则
解得:
答:父子俩今年分别是23岁和45岁。
课后作业
B组题解析:
3)解法二:如图所示,无论是哪一年,父子年龄差不变。
故年龄差=(67-1)÷3=22(岁)
所以,22+1=23(岁)………儿子
22+23=45(岁)………父亲
答:父子俩今年分别是23岁和45岁。
解法三:设父子的年龄差为x岁,则儿子今年(x+1)岁,
父亲今年(2x+1)岁,父亲x年后67岁,则
2x+1+x=67, x=22. ∴ x+1=23, 2x+1=45
答:父子俩今年分别是23岁和45岁。
谢谢大家的配合
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
