2021-2022学年数学苏教版(2019)必修第一册第7章 三角函数 单元综合测试卷(Word含答案解析)
文档属性
| 名称 | 2021-2022学年数学苏教版(2019)必修第一册第7章 三角函数 单元综合测试卷(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 763.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 20:54:06 | ||
图片预览




文档简介
第7章 三角函数 单元综合测试卷
一、单选题。本大题共8小题,每小题只有一个选项符合题意。
1.设MP,OM和AT分别是角的正弦线、余弦线和正切线,则下列式子正确的是( )
A. B.
C. D.
2.点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如果函数y=3cos(2x+φ)的图象关于点对称,那么|φ|的最小值为( )
A. B.
C. D.
4.如图,为一半径为3m的水轮,水轮圆心O距离水面2m,已知水轮自点A开始1min旋转4圈,水轮上的点P到水面距离y(m)与时间x(s)满足函数关系y=Asin(ωx+φ)+2,则有( )
A.ω=,A=3 B.ω=,A=3
C.ω=,A=5 D.ω=,A=5
5.同时具有性质“(1)最小正周期是π;(2)图象关于直线x=对称;(3)在上单调递增”的一个函数是( )
A.y=sin B.y=cos
C.y=sin D.y=cos
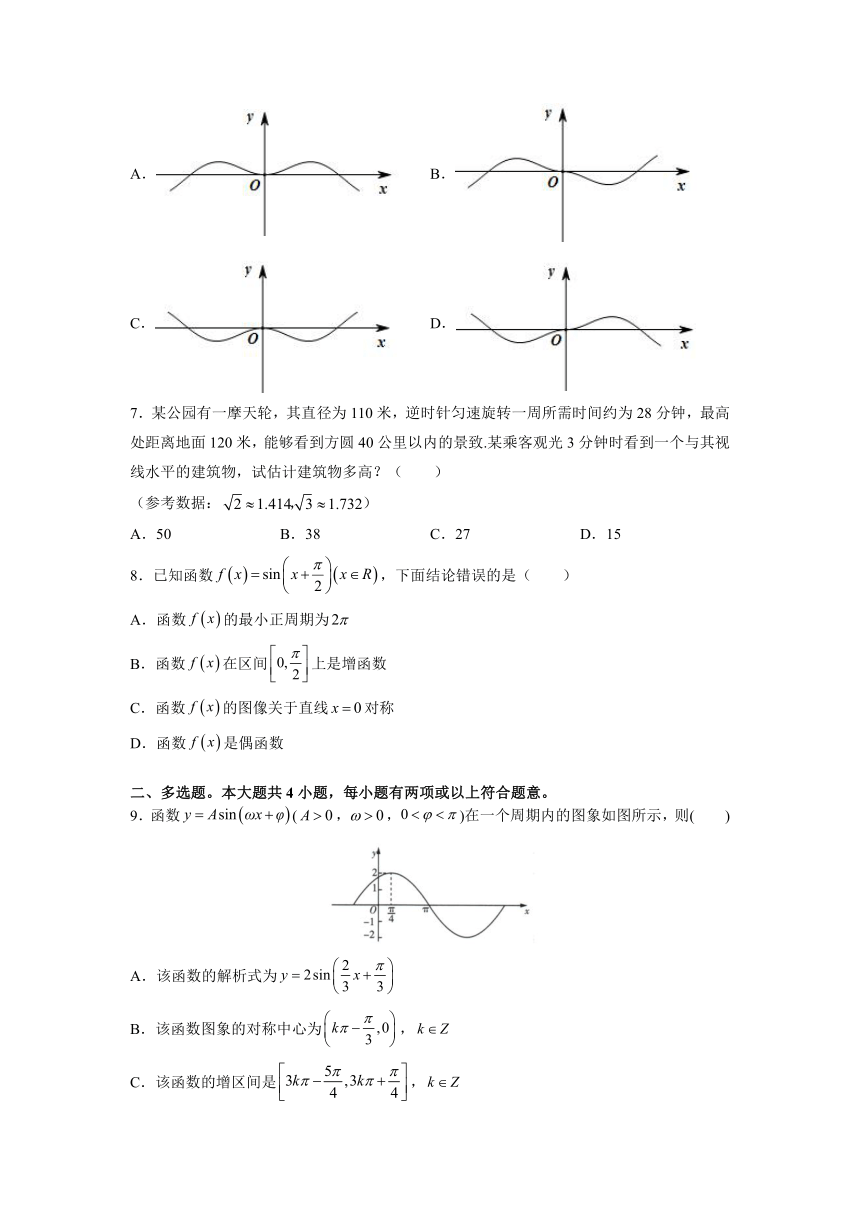
6.函数的部分图象大致形状是( )
A. B.
C. D.
7.某公园有一摩天轮,其直径为110米,逆时针匀速旋转一周所需时间约为28分钟,最高处距离地面120米,能够看到方圆40公里以内的景致.某乘客观光3分钟时看到一个与其视线水平的建筑物,试估计建筑物多高?( )
(参考数据:)
A.50 B.38 C.27 D.15
8.已知函数,下面结论错误的是( )
A.函数的最小正周期为
B.函数在区间上是增函数
C.函数的图像关于直线对称
D.函数是偶函数
二、多选题。本大题共4小题,每小题有两项或以上符合题意。
9.函数(,,)在一个周期内的图象如图所示,则( )
A.该函数的解析式为
B.该函数图象的对称中心为,
C.该函数的增区间是,
D.把函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象
10.已知函数(其中)的图象关于点成中心对称,且与点相邻的一个最低点为,则下列判断正确的是( )
A.函数中
B.直线是函数图象的一条对称轴
C.点是函数的一个对称中心
D.函数与的图象的所有交点的横坐标之和为
11.如图,摩天轮的半径为,其中心点距离地面的高度为,摩天轮按逆时针方向匀速转动,且转一圈,若摩天轮上点的起始位置在最高点处,则摩天轮转动过程中( )
A.转动后点距离地面
B.若摩天轮转速减半,则转动一圈所需的时间变为原来的
C.第和第点距离地面的高度相同
D.摩天轮转动一圈,点距离地面的高度不低于的时间为
12.声音是由物体振动产生的声波,纯音的数学模型是函数,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数,则下列结论正确的是( )
A.是偶函数 B.的最小正周期为
C.在区间上单调递增 D.的最小值为1
三、填空题。本大题共4小题。
13.已知,则的值为______.
14.已知,,则______.
15.关于有如下说法:
①若f(x1)=f(x2)=0,则x1x2是π的整数倍,
②函数解析式可改为,
③函数图象关于对称,
④函数图象关于点对称.
其中正确的是____(填正确的序号)
16.已知角φ的终边经过点P(,-1),点A(x1,y1),B(x2,y2)是函数f(x)=sin(ωx+φ)(ω>0)图象上的任意两点,若|f(x1)-f(x2)|=2时,|x1-x2|的最小值为,则f=________.
四、解答题。本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程。
17.函数(,)的部分图象如图所示.
(1)求的值及的增区间;
(2)若图象的横坐标不变,纵坐标扩大为原来的2倍,然后再将所得图象向右平移个单位长度,最后向上平移1个单位长度,得到函数的图象,若在上函数的图象与x轴恰有10个交点,求实数b的取值范围.
18.如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图象的一部分,后一段DBC是函数(,,,)的图象,图象的最高点为,且,垂足为点F.
(1)求函数()的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为,点E在OC上,求儿童乐园的面积.
19.已知函数(,,),在同一个周期内,当时,y取最大值1,当时,y取最小值-1.
(1)求函数的解析式.
(2)函数的图象经过怎样的变换可得到的图象
(3)求方程在内的所有实数根之和.
20.设函数的部分图象如图所示,求的表达式.
21.若sin=,cos=,且0<α<<β<,求cos(α+β)的值.
22.已知函数f(x)=2cos2,g(x)=2.
(1)求证:f=g(x);
(2)求函数h(x)=f(x)-g(x)(x∈[0,π]的单调区间,并求使h(x)取到最小值时x的值.
参考答案
1.B
【解析】解:分别作角的正弦线、余弦线和正切线,如图,
∵,,.
∴.
故选:B.
2.C
【解析】∵,
∴913°角为第三象限角,
∴,,
∴点位于第三象限.
故选:C.
3.A
【解析】因函数y=3cos(2x+φ)的图象关于点对称,则有,
于是得,显然对于是递增的,
而时,,,当时,,,
所以|φ|的最小值为.
故选:A
4.A
【解析】由题目可知最大值为5,∴ 5=A×1+2 A=3.
,则.故选:A
5.C
【解析】由(1)知T=π=,ω=2,排除A.
由(2)(3)知x=时,f(x)取最大值,
对于B,当时,,取到最小值,不合题意,
对于C,当时,,符合题意,
对于D,当时,,不合题意,
故选:C
6.C
【解析】定义域为,关于原点对称,
,
所以是偶函数,图象关于轴对称,故排除选项B、D;
当时,令可得或,
所以时,两个相邻的零点为和,
当时,,,,
故排除选项A,
故选:C.
7.C
【解析】设走了3分钟到达(如图所示),
走过的圆心角为,
,
因为 ,
所以,
所以
所以,
所以建筑物的高度:
故选:C
8.B
【解析】解:,
对于A,的最小正周期为,所以A正确;
对于B,在区间上是减函数,所以B错误;
对于C,因为,所以的图像关于直线对称,所以C正确;
对于D,因为,所以是偶函数,所以D正确,
故选:B
9.ACD
【解析】由题图可知,,周期,
所以,则,
因为当时,,即,
所以,,即,,
又,故,
从而,故A正确;
令,,得,,故B错误;
令,,
得,,故C正确;
函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,
可得到,故D正确.
故选:ACD.
10.ACD
【解析】解:函数(其中,,的图象关于点成中心对称,且与点相邻的一个最低点为,
则,
,
进一步解得,,故A正确.
由于函数(其中,,的图象关于点成中心对称,
,
解得,
由于,
当时,.
.
对于B:当时,,故B不正确;
对于C:由,,解得,,
当时,对称中心为:,故C正确;
对于D:由于:,
则:,
函数的图象与有6个交点.
根据函数的交点设横坐标从左到右分别为、、、、、,
由,,解得,,
所以,,,
所以
所以函数的图象的所有交点的横坐标之和为,故D正确.
正确的判断是ACD.
故选:ACD.
11.AC
【解析】解:摩天轮转一圈,
在内转过的角度为,
建立平面直角坐标系,如图,
设是以轴正半轴为始边,表示点的起始位置为终边的角,
以轴正半轴为始边,为终边的角为,
即点的纵坐标为,
又由题知,点起始位置在最高点处,
点距地面高度关于旋转时间的函数关系式为:
即
当时,,故A正确;
若摩天轮转速减半,,则其周期变为原来的2倍,故B错误;
第点距安地面的高度为
第点距离地面的高度为
第和第时点距离地面的高度相同,故C正确;
摩天轮转动一圈,点距离地面的高度不低于,
即,
即,,
得,
或,
解得或,
共,故D错误.
故选:AC.
12.AD
【解析】因为,,所以是偶函数,A正确;
显然是周期函数,
因为,所以B错误;
因为当时,
,
所以在区间上单调递增,在上单调递减,C错误;
因为
当时,设,则,∴,∴,
同理:当时,,
由B中解答知,是的周期,所以的最小值为1,D正确.
故选:AD.
13.2
【解析】原式
.
故答案为:
14.
【解析】因为,,
所以,
所以,
故答案为:
15.②③
【解析】①若f(x1)=f(x2)=0,则x1x2是半个周期的整数倍,而函数 的周期为π,故x1x2是的整数倍,故不正确.
②函数解析式,故正确.
③当时,y=3是函数的最小值,故函数图象关于对称,故正确.
④当 时,y=3是函数的最大值,故函数图象关于 对称,故不正确.
故答案为:②③.
16.-
【解析】由条件|f(x1)-f(x2)|=2时,|x1-x2|的最小值为,可知函数f(x)的最小正周期为
,则由,得ω=3.又因为角φ的终边经过点P(,-1),
,,,所以不妨取φ=-,
则f(x)=sin,于是f=sin=-.
故答案为:-.
17.
(1);(2)
解:(2)由题意知.
令,即,即或,得或.
所以在上函数的图象与x轴恰有两个交点,若在上函数的图象与x轴恰有10个交点,则b不小于第10个交点的横坐标,小于第11个交点的横坐标,
即b的取值范围为且,解得.
故实数b的取值范围为.
18.
(1),(2)
19.
(1)(2)答案见解析(3)
20..
【解析】由图象可得,,
∴,从而,
又∵点在函数的图象上,∴,
从而,即,
∵,∴,
故的表达式:.
故答案为:.
21.-.
【解析】解: ∵0<α<<β<,
∴<+α<π,-<-β<0.
又sin=,cos=,
∴cos=-,sin=-,
∴cos(α+β)=sin=sin
=sincos-cossin
=.
22.(1)证明见解析;(2)单调递减区间为,单调递增区间为,当x=时,函数h(x)取到最小值.
【解析】(1)因为,
,
,
所以.
(2)函数,
∵,如图,结合函数的图像,
∴函数h(x)在的单调递减区间为,单调递增区间为,
根据函数h(x)的单调性,可知当x=时,函数h(x)取到最小值.
一、单选题。本大题共8小题,每小题只有一个选项符合题意。
1.设MP,OM和AT分别是角的正弦线、余弦线和正切线,则下列式子正确的是( )
A. B.
C. D.
2.点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如果函数y=3cos(2x+φ)的图象关于点对称,那么|φ|的最小值为( )
A. B.
C. D.
4.如图,为一半径为3m的水轮,水轮圆心O距离水面2m,已知水轮自点A开始1min旋转4圈,水轮上的点P到水面距离y(m)与时间x(s)满足函数关系y=Asin(ωx+φ)+2,则有( )
A.ω=,A=3 B.ω=,A=3
C.ω=,A=5 D.ω=,A=5
5.同时具有性质“(1)最小正周期是π;(2)图象关于直线x=对称;(3)在上单调递增”的一个函数是( )
A.y=sin B.y=cos
C.y=sin D.y=cos
6.函数的部分图象大致形状是( )
A. B.
C. D.
7.某公园有一摩天轮,其直径为110米,逆时针匀速旋转一周所需时间约为28分钟,最高处距离地面120米,能够看到方圆40公里以内的景致.某乘客观光3分钟时看到一个与其视线水平的建筑物,试估计建筑物多高?( )
(参考数据:)
A.50 B.38 C.27 D.15
8.已知函数,下面结论错误的是( )
A.函数的最小正周期为
B.函数在区间上是增函数
C.函数的图像关于直线对称
D.函数是偶函数
二、多选题。本大题共4小题,每小题有两项或以上符合题意。
9.函数(,,)在一个周期内的图象如图所示,则( )
A.该函数的解析式为
B.该函数图象的对称中心为,
C.该函数的增区间是,
D.把函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象
10.已知函数(其中)的图象关于点成中心对称,且与点相邻的一个最低点为,则下列判断正确的是( )
A.函数中
B.直线是函数图象的一条对称轴
C.点是函数的一个对称中心
D.函数与的图象的所有交点的横坐标之和为
11.如图,摩天轮的半径为,其中心点距离地面的高度为,摩天轮按逆时针方向匀速转动,且转一圈,若摩天轮上点的起始位置在最高点处,则摩天轮转动过程中( )
A.转动后点距离地面
B.若摩天轮转速减半,则转动一圈所需的时间变为原来的
C.第和第点距离地面的高度相同
D.摩天轮转动一圈,点距离地面的高度不低于的时间为
12.声音是由物体振动产生的声波,纯音的数学模型是函数,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数,则下列结论正确的是( )
A.是偶函数 B.的最小正周期为
C.在区间上单调递增 D.的最小值为1
三、填空题。本大题共4小题。
13.已知,则的值为______.
14.已知,,则______.
15.关于有如下说法:
①若f(x1)=f(x2)=0,则x1x2是π的整数倍,
②函数解析式可改为,
③函数图象关于对称,
④函数图象关于点对称.
其中正确的是____(填正确的序号)
16.已知角φ的终边经过点P(,-1),点A(x1,y1),B(x2,y2)是函数f(x)=sin(ωx+φ)(ω>0)图象上的任意两点,若|f(x1)-f(x2)|=2时,|x1-x2|的最小值为,则f=________.
四、解答题。本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程。
17.函数(,)的部分图象如图所示.
(1)求的值及的增区间;
(2)若图象的横坐标不变,纵坐标扩大为原来的2倍,然后再将所得图象向右平移个单位长度,最后向上平移1个单位长度,得到函数的图象,若在上函数的图象与x轴恰有10个交点,求实数b的取值范围.
18.如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图象的一部分,后一段DBC是函数(,,,)的图象,图象的最高点为,且,垂足为点F.
(1)求函数()的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为,点E在OC上,求儿童乐园的面积.
19.已知函数(,,),在同一个周期内,当时,y取最大值1,当时,y取最小值-1.
(1)求函数的解析式.
(2)函数的图象经过怎样的变换可得到的图象
(3)求方程在内的所有实数根之和.
20.设函数的部分图象如图所示,求的表达式.
21.若sin=,cos=,且0<α<<β<,求cos(α+β)的值.
22.已知函数f(x)=2cos2,g(x)=2.
(1)求证:f=g(x);
(2)求函数h(x)=f(x)-g(x)(x∈[0,π]的单调区间,并求使h(x)取到最小值时x的值.
参考答案
1.B
【解析】解:分别作角的正弦线、余弦线和正切线,如图,
∵,,.
∴.
故选:B.
2.C
【解析】∵,
∴913°角为第三象限角,
∴,,
∴点位于第三象限.
故选:C.
3.A
【解析】因函数y=3cos(2x+φ)的图象关于点对称,则有,
于是得,显然对于是递增的,
而时,,,当时,,,
所以|φ|的最小值为.
故选:A
4.A
【解析】由题目可知最大值为5,∴ 5=A×1+2 A=3.
,则.故选:A
5.C
【解析】由(1)知T=π=,ω=2,排除A.
由(2)(3)知x=时,f(x)取最大值,
对于B,当时,,取到最小值,不合题意,
对于C,当时,,符合题意,
对于D,当时,,不合题意,
故选:C
6.C
【解析】定义域为,关于原点对称,
,
所以是偶函数,图象关于轴对称,故排除选项B、D;
当时,令可得或,
所以时,两个相邻的零点为和,
当时,,,,
故排除选项A,
故选:C.
7.C
【解析】设走了3分钟到达(如图所示),
走过的圆心角为,
,
因为 ,
所以,
所以
所以,
所以建筑物的高度:
故选:C
8.B
【解析】解:,
对于A,的最小正周期为,所以A正确;
对于B,在区间上是减函数,所以B错误;
对于C,因为,所以的图像关于直线对称,所以C正确;
对于D,因为,所以是偶函数,所以D正确,
故选:B
9.ACD
【解析】由题图可知,,周期,
所以,则,
因为当时,,即,
所以,,即,,
又,故,
从而,故A正确;
令,,得,,故B错误;
令,,
得,,故C正确;
函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,
可得到,故D正确.
故选:ACD.
10.ACD
【解析】解:函数(其中,,的图象关于点成中心对称,且与点相邻的一个最低点为,
则,
,
进一步解得,,故A正确.
由于函数(其中,,的图象关于点成中心对称,
,
解得,
由于,
当时,.
.
对于B:当时,,故B不正确;
对于C:由,,解得,,
当时,对称中心为:,故C正确;
对于D:由于:,
则:,
函数的图象与有6个交点.
根据函数的交点设横坐标从左到右分别为、、、、、,
由,,解得,,
所以,,,
所以
所以函数的图象的所有交点的横坐标之和为,故D正确.
正确的判断是ACD.
故选:ACD.
11.AC
【解析】解:摩天轮转一圈,
在内转过的角度为,
建立平面直角坐标系,如图,
设是以轴正半轴为始边,表示点的起始位置为终边的角,
以轴正半轴为始边,为终边的角为,
即点的纵坐标为,
又由题知,点起始位置在最高点处,
点距地面高度关于旋转时间的函数关系式为:
即
当时,,故A正确;
若摩天轮转速减半,,则其周期变为原来的2倍,故B错误;
第点距安地面的高度为
第点距离地面的高度为
第和第时点距离地面的高度相同,故C正确;
摩天轮转动一圈,点距离地面的高度不低于,
即,
即,,
得,
或,
解得或,
共,故D错误.
故选:AC.
12.AD
【解析】因为,,所以是偶函数,A正确;
显然是周期函数,
因为,所以B错误;
因为当时,
,
所以在区间上单调递增,在上单调递减,C错误;
因为
当时,设,则,∴,∴,
同理:当时,,
由B中解答知,是的周期,所以的最小值为1,D正确.
故选:AD.
13.2
【解析】原式
.
故答案为:
14.
【解析】因为,,
所以,
所以,
故答案为:
15.②③
【解析】①若f(x1)=f(x2)=0,则x1x2是半个周期的整数倍,而函数 的周期为π,故x1x2是的整数倍,故不正确.
②函数解析式,故正确.
③当时,y=3是函数的最小值,故函数图象关于对称,故正确.
④当 时,y=3是函数的最大值,故函数图象关于 对称,故不正确.
故答案为:②③.
16.-
【解析】由条件|f(x1)-f(x2)|=2时,|x1-x2|的最小值为,可知函数f(x)的最小正周期为
,则由,得ω=3.又因为角φ的终边经过点P(,-1),
,,,所以不妨取φ=-,
则f(x)=sin,于是f=sin=-.
故答案为:-.
17.
(1);(2)
解:(2)由题意知.
令,即,即或,得或.
所以在上函数的图象与x轴恰有两个交点,若在上函数的图象与x轴恰有10个交点,则b不小于第10个交点的横坐标,小于第11个交点的横坐标,
即b的取值范围为且,解得.
故实数b的取值范围为.
18.
(1),(2)
19.
(1)(2)答案见解析(3)
20..
【解析】由图象可得,,
∴,从而,
又∵点在函数的图象上,∴,
从而,即,
∵,∴,
故的表达式:.
故答案为:.
21.-.
【解析】解: ∵0<α<<β<,
∴<+α<π,-<-β<0.
又sin=,cos=,
∴cos=-,sin=-,
∴cos(α+β)=sin=sin
=sincos-cossin
=.
22.(1)证明见解析;(2)单调递减区间为,单调递增区间为,当x=时,函数h(x)取到最小值.
【解析】(1)因为,
,
,
所以.
(2)函数,
∵,如图,结合函数的图像,
∴函数h(x)在的单调递减区间为,单调递增区间为,
根据函数h(x)的单调性,可知当x=时,函数h(x)取到最小值.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
