鲁教版(五四学制)数学六年级上册第二章 有理数及其运算 2.3绝对值 课件(共17张PPT)
文档属性
| 名称 | 鲁教版(五四学制)数学六年级上册第二章 有理数及其运算 2.3绝对值 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 178.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 14:14:06 | ||
图片预览




文档简介
(共17张PPT)
3 绝对值
0
1
2
3
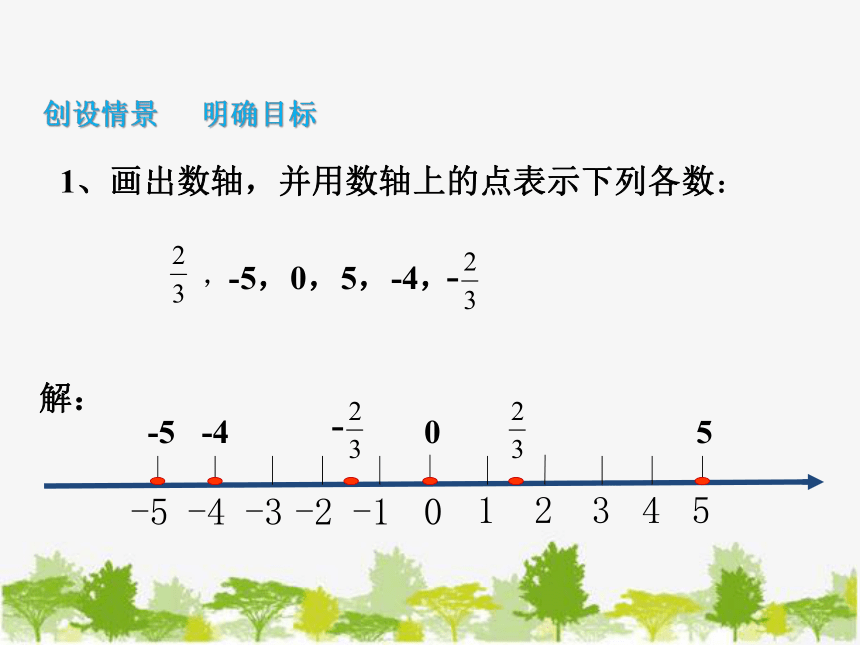
解:
1、画出数轴,并用数轴上的点表示下列各数:
-5,0,5,-4,
,
4
5
-5
-4
-3
-2
-1
-
-
-5
0
5
-4
创设情景 明确目标
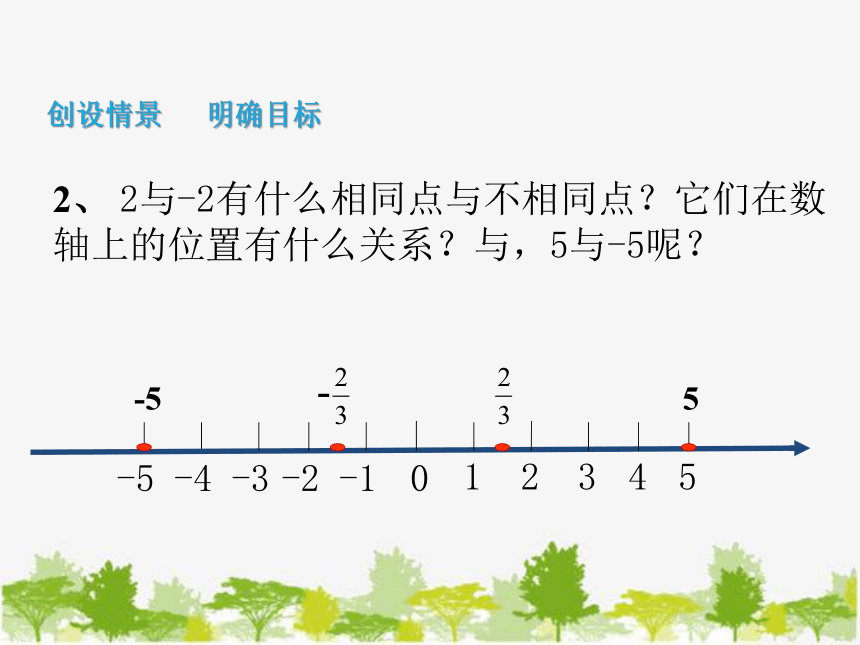
2、 2与-2有什么相同点与不相同点?它们在数轴上的位置有什么关系?与,5与-5呢?
0
1
2
3
4
5
-5
-4
-3
-2
-1
-
-5
5
创设情景 明确目标
1.借助数轴,初步理解绝对值和相反数的概念,能求一个数的绝对值和相反数.
2.会利用绝对值比较两负数的大小;学习数形结合的数学方法和分类讨论的思想.
学习目标
结论
如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数。特别地,0的相反数是0。
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点的距离相等。
西
东
3
3
A
O
B
0
3
-3
1
2
-2
-1
3米
3米
路线不同,正负性
路程一样,到原点的距离相等(不管方向)
它们所跑的路线相同吗?
它们所跑的路程(线段OA、OB的长度)一样吗?
在数轴上表示出这一情景.
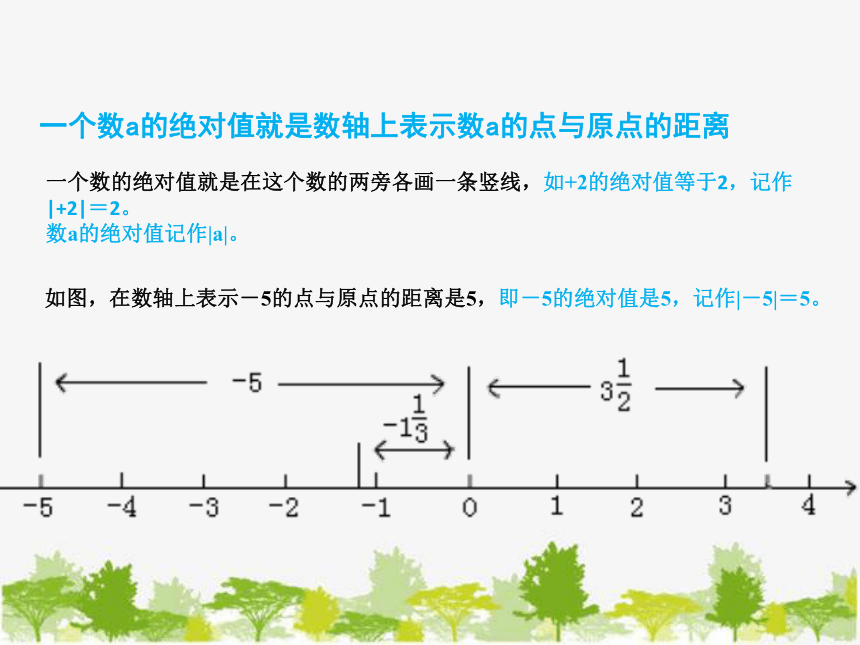
一个数a的绝对值就是数轴上表示数a的点与原点的距离
一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2。
数a的绝对值记作|a|。
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
活动一:1. 阅读教材,思考:+3与-3,-5与+5,-1.5与1.5这三对数有什么共同点?还能列举出这样的数吗?如何表示相反数?
2. 在数轴上,标出以下各数及它们的相反数-1,0, ,-4.思考:数轴上表示互为相反数的两个点到原点的距离有何关系?
探究点一:相反数的概念
合作探究 达成目标
探究点一:相反数的概念
合作探究 达成目标
【展示点评】1.如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.特别地,0的相反数是0.如,+3的相反数是-3,也可以说+3与-3互为相反数.相反数是成对出现的,不能单独存在.
2. 相反数的表示方法:如6的相反数是-6,即在6的前面添加一个“-”号,那么-3的相反数就可以表示成-(-3)=+3.
3. 相反数的几何特征:(1)分别位于原点的两侧;(2)与原点的距离相等.
【小组讨论1】化简下列各数的符号:
-(- );-(+3.5);+(-0.3);-[+(-7)].
探究点一:相反数的概念
合作探究 达成目标
【反思小结】1.在一个数前面添一个“+”号,仍然与原数相同,如+5=5.2.在一个数前面添一个“—”号,就变成原数的相反数,如-(-3)就表示-3的相反数,因此-(-3)=3.3.符号的化简,只需要考虑负号的个数,当有奇数个负号时,结果为负;当有偶数个负号时结果为正.
解:;-3.5;-0.3;7.
活动二:阅读教材,探究解决:
画数轴,观察回答:
距原点1个单位长度的数是_________和_________,
距原点2个单位长度的数是____________和__________,
距原点 个单位长度的数是________和________,
距原点4个单位长度的数是_________和_________.
距原点最近的是__________.
【展示点评】像1,2, ,4,0分别是±1,±2,± ,±4,0的绝对值.在数轴上,一个数所对应的点与原点的距离叫该数的绝对值.
如:+2的绝对值是2,记作|+2|=2;-2的绝对值是2,记作|-2|=2.
探究点二:绝对值的概念及求法
合作探究 达成目标
+1
-1
+2
+
+4
0
-2
-
-4
【小组讨论2】求下列各数的绝对值:-1.5,1.5,-6,+6,-3,3, 0.
合作探究 达成目标
【反思小结】归纳:正数的绝对值是______;负数的绝对值是__________;零的绝对值是______.
注意:1.互为相反数的两数的绝对值相等.
2.有理数的绝对值不可能是负数,即|a |≥0.
探究点二:绝对值的概念及求法
活动三:比较两负数的大小:
(1)在数轴上表示下列各数,并比较大小:
- 2.5 , - 4 , - 1 ,0
(2)求出(1)中各数的绝对值,并比较它们的大
小
(3)你发现了什么?
【展示点评】两个负数比较大小,绝对值大的反而小.
探究点三:利用绝对值比较两个负数的大小
合作探究 达成目标
【小组讨论3】阅读教材第31页例2,思考:比较两负数的大小,一般有哪些步骤?拓展思考:非负数有何性质,例如两个非负数的和为0,那么你能由此得出什么判断?
合作探究 达成目标
【反思小结】1. 比较两负数的大小的步骤:(1)分别求出两负数的绝对值;(2)比较这两个数的绝对值大小;(3)根据“两个负数比较大小,绝对值大的反而小”作出判断.
2.非负数的性质:几个非负数的和为0,就是每一个非负数为0.例如,已知|a|+|b|=0,则a=0,b=0.
探究点三:利用绝对值比较两个负数的大小
1.课本知识
(1)只有符号不同的两个数,称其中一个数为另一个数的相反数,也称这两个数互为相反数.特别地,0的相反数是0.如, -(-7)=+7.
(2)相反数的几何特征:①分别位于原点的两侧;②与原点的距离相等.
(3)在数轴上,一个数所对应的点与原点的距离叫该数的绝对值.正数的绝对值是正数;负数的绝对值是正数;零的绝对值是零.| |≥0.
(4)两个负数比较大小,绝对值大的反而小.
2.本课典例:求一个数的绝对值和相反数、符号的化简、几个非负数和为零.
3.我的困惑:
总结梳理 内化目标
达标检测 反思目标
2. 下面各对数中互为相反数的是( )
A.2与-|-2| B.-2与-|2|
C.|-2|与|2| D.2与-(-2)
3. 下面的大小关系不成立的是( )
A.-5.35> B.-(+2)<-( -3)
C.-1.7>-1.777 D.|-3|>|+2|
B
A
A
4.一个数在数轴上表示的点距原点6个单位长度,
且在原点的左边,则这个数的相反数________.
5.绝对值是4的数有______个,它们分别是
_______和_______;绝对值不大于2的整数是
____________.
6
±2,±1,0
2
4
-4
达标检测 反思目标
3 绝对值
0
1
2
3
解:
1、画出数轴,并用数轴上的点表示下列各数:
-5,0,5,-4,
,
4
5
-5
-4
-3
-2
-1
-
-
-5
0
5
-4
创设情景 明确目标
2、 2与-2有什么相同点与不相同点?它们在数轴上的位置有什么关系?与,5与-5呢?
0
1
2
3
4
5
-5
-4
-3
-2
-1
-
-5
5
创设情景 明确目标
1.借助数轴,初步理解绝对值和相反数的概念,能求一个数的绝对值和相反数.
2.会利用绝对值比较两负数的大小;学习数形结合的数学方法和分类讨论的思想.
学习目标
结论
如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数。特别地,0的相反数是0。
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点的距离相等。
西
东
3
3
A
O
B
0
3
-3
1
2
-2
-1
3米
3米
路线不同,正负性
路程一样,到原点的距离相等(不管方向)
它们所跑的路线相同吗?
它们所跑的路程(线段OA、OB的长度)一样吗?
在数轴上表示出这一情景.
一个数a的绝对值就是数轴上表示数a的点与原点的距离
一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2。
数a的绝对值记作|a|。
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
活动一:1. 阅读教材,思考:+3与-3,-5与+5,-1.5与1.5这三对数有什么共同点?还能列举出这样的数吗?如何表示相反数?
2. 在数轴上,标出以下各数及它们的相反数-1,0, ,-4.思考:数轴上表示互为相反数的两个点到原点的距离有何关系?
探究点一:相反数的概念
合作探究 达成目标
探究点一:相反数的概念
合作探究 达成目标
【展示点评】1.如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.特别地,0的相反数是0.如,+3的相反数是-3,也可以说+3与-3互为相反数.相反数是成对出现的,不能单独存在.
2. 相反数的表示方法:如6的相反数是-6,即在6的前面添加一个“-”号,那么-3的相反数就可以表示成-(-3)=+3.
3. 相反数的几何特征:(1)分别位于原点的两侧;(2)与原点的距离相等.
【小组讨论1】化简下列各数的符号:
-(- );-(+3.5);+(-0.3);-[+(-7)].
探究点一:相反数的概念
合作探究 达成目标
【反思小结】1.在一个数前面添一个“+”号,仍然与原数相同,如+5=5.2.在一个数前面添一个“—”号,就变成原数的相反数,如-(-3)就表示-3的相反数,因此-(-3)=3.3.符号的化简,只需要考虑负号的个数,当有奇数个负号时,结果为负;当有偶数个负号时结果为正.
解:;-3.5;-0.3;7.
活动二:阅读教材,探究解决:
画数轴,观察回答:
距原点1个单位长度的数是_________和_________,
距原点2个单位长度的数是____________和__________,
距原点 个单位长度的数是________和________,
距原点4个单位长度的数是_________和_________.
距原点最近的是__________.
【展示点评】像1,2, ,4,0分别是±1,±2,± ,±4,0的绝对值.在数轴上,一个数所对应的点与原点的距离叫该数的绝对值.
如:+2的绝对值是2,记作|+2|=2;-2的绝对值是2,记作|-2|=2.
探究点二:绝对值的概念及求法
合作探究 达成目标
+1
-1
+2
+
+4
0
-2
-
-4
【小组讨论2】求下列各数的绝对值:-1.5,1.5,-6,+6,-3,3, 0.
合作探究 达成目标
【反思小结】归纳:正数的绝对值是______;负数的绝对值是__________;零的绝对值是______.
注意:1.互为相反数的两数的绝对值相等.
2.有理数的绝对值不可能是负数,即|a |≥0.
探究点二:绝对值的概念及求法
活动三:比较两负数的大小:
(1)在数轴上表示下列各数,并比较大小:
- 2.5 , - 4 , - 1 ,0
(2)求出(1)中各数的绝对值,并比较它们的大
小
(3)你发现了什么?
【展示点评】两个负数比较大小,绝对值大的反而小.
探究点三:利用绝对值比较两个负数的大小
合作探究 达成目标
【小组讨论3】阅读教材第31页例2,思考:比较两负数的大小,一般有哪些步骤?拓展思考:非负数有何性质,例如两个非负数的和为0,那么你能由此得出什么判断?
合作探究 达成目标
【反思小结】1. 比较两负数的大小的步骤:(1)分别求出两负数的绝对值;(2)比较这两个数的绝对值大小;(3)根据“两个负数比较大小,绝对值大的反而小”作出判断.
2.非负数的性质:几个非负数的和为0,就是每一个非负数为0.例如,已知|a|+|b|=0,则a=0,b=0.
探究点三:利用绝对值比较两个负数的大小
1.课本知识
(1)只有符号不同的两个数,称其中一个数为另一个数的相反数,也称这两个数互为相反数.特别地,0的相反数是0.如, -(-7)=+7.
(2)相反数的几何特征:①分别位于原点的两侧;②与原点的距离相等.
(3)在数轴上,一个数所对应的点与原点的距离叫该数的绝对值.正数的绝对值是正数;负数的绝对值是正数;零的绝对值是零.| |≥0.
(4)两个负数比较大小,绝对值大的反而小.
2.本课典例:求一个数的绝对值和相反数、符号的化简、几个非负数和为零.
3.我的困惑:
总结梳理 内化目标
达标检测 反思目标
2. 下面各对数中互为相反数的是( )
A.2与-|-2| B.-2与-|2|
C.|-2|与|2| D.2与-(-2)
3. 下面的大小关系不成立的是( )
A.-5.35> B.-(+2)<-( -3)
C.-1.7>-1.777 D.|-3|>|+2|
B
A
A
4.一个数在数轴上表示的点距原点6个单位长度,
且在原点的左边,则这个数的相反数________.
5.绝对值是4的数有______个,它们分别是
_______和_______;绝对值不大于2的整数是
____________.
6
±2,±1,0
2
4
-4
达标检测 反思目标
