3.1 一元二次方程

(共14张PPT)
九年级数学(上)第三章： 一元二次方程
3.1 一元二次方程（1）
1、正确理解一元二次方程的概念，掌握一元二次
方程的一般形式。
2、进一步体会方程是刻画现实世界中数量关系的
一个有效数学模型。
3、能将一元二次方程转化为一般形式，正确识别
二次项系数、一次项系数及常数项。
(1)、某教室的面积为54m2，周长为30m.求该教室的长与宽.
设该教室的长为xm,由它的周长为30m可知，它的宽为________m.
根据问题中的等量关系：长x宽=教室的面积
可以得到方程_____________________.
(2)、直角三角形斜边的长为11cm,两直角边的差为7cm.求两直角边的长.
设较短直角边的长为x(cm),由两条直角边的差为7cm可知，较长直
角边长是_________.
根据问题中的等量关系：两直角边的平方和=斜边的平方，
可以得到方程_______________.
(3)、如图，点c是线段AB上的一点，且
设AB=1,AC=x,则CB的长为_______.
根据问题中的等量关系 , 即AC2=AB·CB
可以得到方程__________________.
A C B
x+7
x2+(x+7)2=112
1-x
x2=1-x
1、三个方程有什么共同特征？ 2、三个方程与一元一次方程有什么相同点和不同点？
整理后得到的方程分别是：
x2-15x+54=0,
x2+7x-36=0,
x2+x-1=0.
①只含有一个未知数;
②未知数的最高次数是2；
③都是整式方程.
三个方程的共同特征：
判断一元二次方程的三个条件:
下列方程哪些是一元二次方程
(2)、2x2－5xy＋6y＝0
(5)、x2＋2x－3＝1＋x2
(1)、7x2－6x＝0
(3)、2x2－ －1 ＝0
－
1
3x
(4) 、 ＝0
－
y2
2
√
×
×
√
×
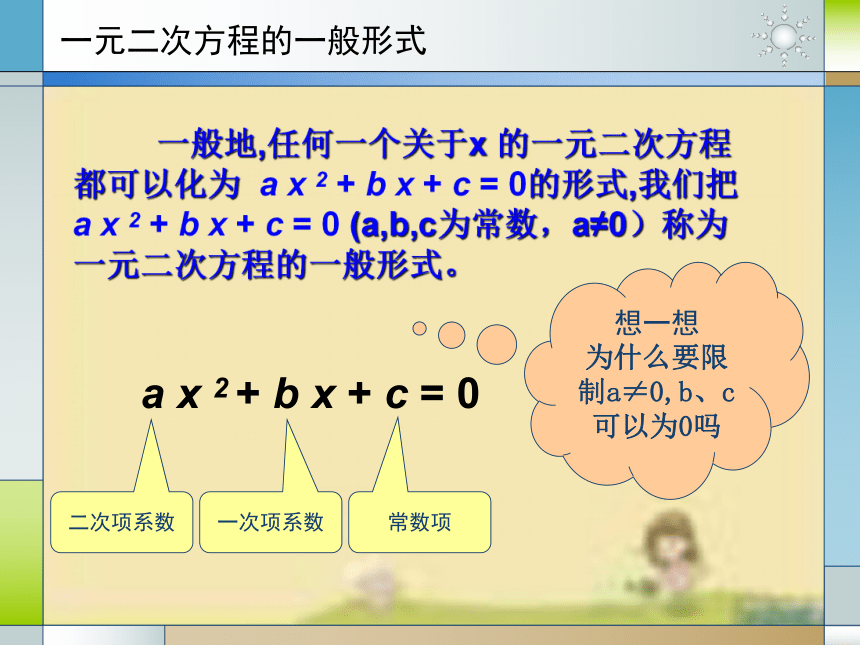
一元二次方程的一般形式
一般地,任何一个关于x 的一元二次方程都可以化为 a x 2 + b x + c = 0的形式,我们把 a x 2 + b x + c = 0 (a,b,c为常数，a≠0）称为一元二次方程的一般形式。
a x 2 + b x + c = 0
二次项系数
一次项系数
常数项
想一想
为什么要限制a≠0,b、c可以为0吗
学以致用
分别说出下列方程的二次项、一次项和常数项及它们的系数
x2-15x+54=0,
x2+7x-36=0,
x2+x-1=0.
将下列方程化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项。
(1)、3x(x-1)=5(x+2)
(2)、(3x+2)(x+1)=8x-3
(3)、(2x+3)(2x-3)=4x
1、选择题
（1）方程(m-1)x2+mx+1=0为关于x的一元二次方程，则
m的值为（ ）
A、任何实数 B、m≠0
C、m ≠ 1 D、m ≠ 0且m ≠ 1
（2）关于x的方程中，一定是一元二次方程的是（ ）
A、ax2+bx+c=0 B、mx2+m-m2=0
C、(m+1)x2=(m+1)2 D、(m2+1)x2-m2=0
2、将下列方程化为一般形式，并分别指出它们的二次项
系数、一次项系数及常数项。
(1)(2x+3)(2x-3)=4x (2)(2x+1)2=64
C
D
1、方程（2a-4)x2-2bx+a=0,在什么条件下为一元
二次方程？什么条件下为一元一次方程？
2、若关于x的方程(m+3)xm -7+(m-5)x+5=0是一
元二次方程，求m的值。
3、求证：关于x的方程
（m2-8m+17)x2+2mx+1=0.不论m取何值，该方
程都是一元二次方程。
2
(a≠0)？
1、本节学习的数学知识是： （1）一元二次方程的概念
（2）一元二次方程的一般形式
2、学习的数学思想方法是：转化、类比思想
3、如何理解一元二次方程的一般形式
（1）(a≠0)是成为一元二次方程的必要条件。
（2）找一元二次方程的二次项、一次项系数及常数项
要先化为一般式。
（3）一元二次方程的项及其系数要包括其前面的符
号。
1、必做题：课本79页习题 第1、2题
2、选做题：
（1）当x取何值时，方程
是关于x的一元二次方程？
（2）已知关于 x的一元二次方程
写出它的各项系数，并指出字母 的取值范围。