25.1.1 随机事件 同步测试卷 2021—2022学年人教版九年级数学上册(word版 含答案)
文档属性
| 名称 | 25.1.1 随机事件 同步测试卷 2021—2022学年人教版九年级数学上册(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 297.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 12:50:05 | ||
图片预览



文档简介
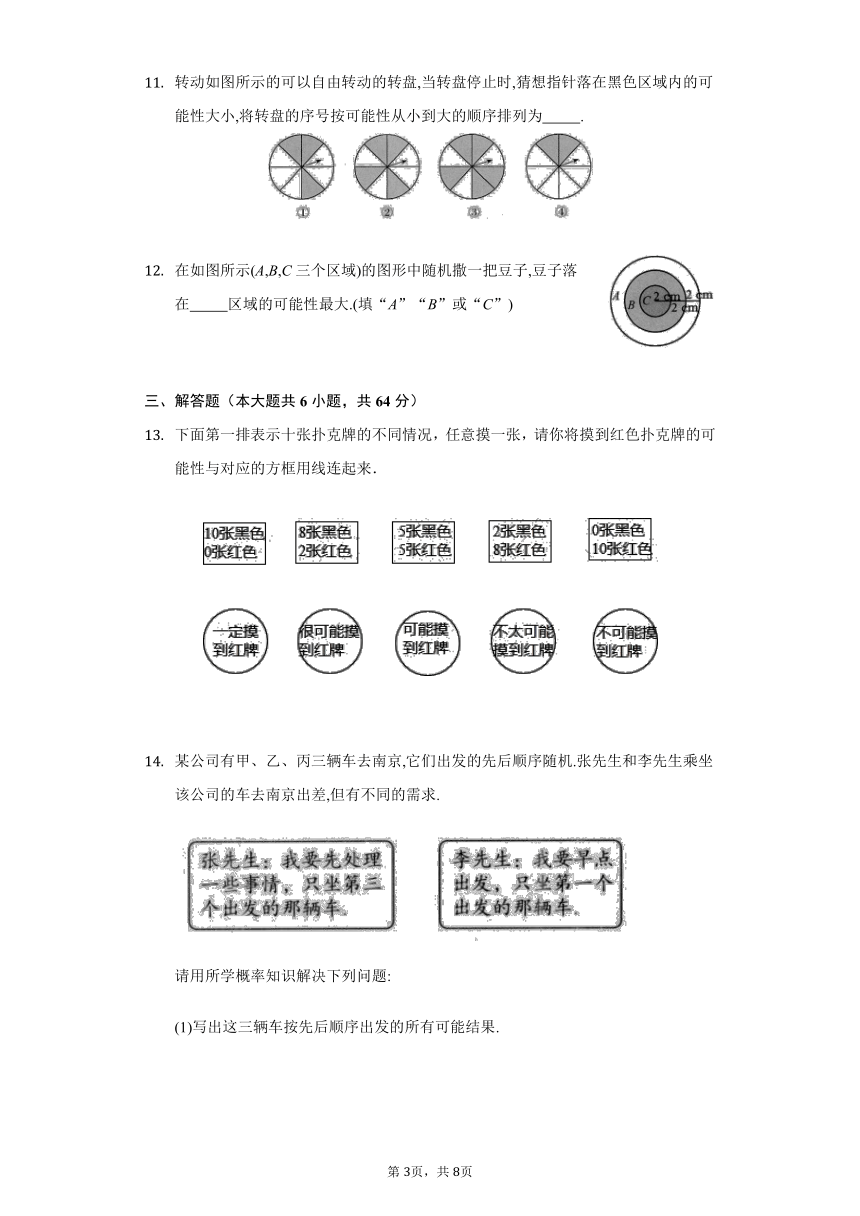
25.1.1 随机事件同步测试卷 2021—2022学年人教版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共27分)
下列事件中是不可能事件的是( )
A. 守株待兔 B. 瓮中捉鳖 C. 水中捞月 D. 百步穿杨
下列事件是必然事件的为( )
A. 任意一个五边形的外角和为
B. 抛掷一枚均匀的硬币次,正面朝上的次数为
C. 个人中至少有两个人的出生月份是相同的
D. 太阳从西方升起
两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3,从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )
A. 两个小球的标号之和等于 B. 两个小球的标号之和等于
C. 两个小球的标号之和大于 D. 两个小球的标号之和大于
某商贩设计了一个转盘游戏,游戏规则如下:
游戏规则
转动转盘,若指针停在偶数所在区域,则停止游戏;若指针停在奇数所在区域,则抽出一个弹珠,当弹珠为黑色时,得百元大奖,否则游戏结束.
转盘和袋子里的弹珠如图所示,某位游客想玩这个游戏,则他获得百元大奖的可能性( )
A. 为 B. 约为 C. 非常小 D. 约为
抛掷一枚质地均匀的硬币2000次,正面朝上的次数最有可能为( )
A. B. C. D.
在一个布袋中装有红、白两种颜色的球, 它们除颜色外没有任何其他区别, 其中红球若干,白球5个,袋中的球已搅匀,若从袋中随机取出一个球,取出红球的可能性大,则红球( )
A. 有个 B. 有个
C. 不足个 D. 有个或个以上
在某校艺体节的乒乓球比赛中,李东同学顺利进入总决赛,且个人技艺高超,有同学预测“李东夺冠的可能性是80%”,对该同学的说法理解正确的是( )
A. 李东夺冠的可能性较小
B. 李东和他的对手比赛局时,他一定赢局
C. 李东夺冠的可能性较大
D. 李东肯定会赢
如图,电路图上有4个开关A,B,C,D和1个小灯泡,同时闭合开关A,B或同时闭合开关C,D都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A. 只闭合个开关 B. 只闭合个开关
C. 只闭合个开关 D. 闭合个开关
如图所示的为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同, 经过四层净化后流入底部的5个出口中的一个.下列判断:
5个出口的出水量相同;
2号出口的出水量与4号出口的出水量相同;
1,2,3号出口的出水量之比约为1:4:6;
若净化材料损耗的速度与流经其表面的水量成正比,则更换最慢的一个三角形材料使用的时间约为更换最快的一个三角形材料使用时间的8倍.
其中正确的判断有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共3小题,共9分)
一个袋中装有6个红球,5个黄球,3个白球,每个球除颜色外都相同,任意摸出一球,摸到______球的可能性最大.
转动如图所示的可以自由转动的转盘,当转盘停止时,猜想指针落在黑色区域内的可能性大小,将转盘的序号按可能性从小到大的顺序排列为 .
在如图所示(A,B,C三个区域)的图形中随机撒一把豆子,豆子落在 区域的可能性最大.(填“A”“B”或“C”)
三、解答题(本大题共6小题,共64分)
下面第一排表示十张扑克牌的不同情况,任意摸一张,请你将摸到红色扑克牌的可能性与对应的方框用线连起来.
某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果.
(2)两人中,谁乘坐到甲车的可能性大 请说明理由.
有12张标有数字2,2,2,3,3,4,4,4,5,5,6,7的卡片,从中任意抽取一张.
(1)抽出的数字是4和5的可能性哪个大?
(2)抽出的数字是奇数和偶数的可能性哪个大?
(3)连续抽5次(抽出后不放回),抽出的五个数组成的五位数最小可能是多少?
已知关于x的二次函数y=-12x+12+2a,设事件A:“x<0时,y随x的增大而减小”,事件B:“二次函数y=-12x+12+2a的图象与x轴有两个交点”.
(1)小聪说A是必然事件,请你说明其中的道理;
(2)小明说B是随机事件,请你说明其中的道理.
某电视节目中有一个游戏环节是大转轮比赛,转轮上平均分布着5,10,15,20,…,95,100共20个数字.选手依次转动转轮,每个人有两次机会.选手中转动的数字之和最大且不超过100者胜出;若超过100则成绩无效,称为“爆掉”.
(1)某选手第一次转到了数字5,再转第二次,则两次数字之和为100的可能性有多大?
(2)现在某选手第一次转到了数字65,若再转第二次,则有可能“爆掉”,请你分析“爆掉”的可能性有多大.
甲、乙两人玩一种游戏:共20张牌,牌面上分别写有-10,-9,-8,…,-1,1,2,…,10,洗好牌后,将背面朝上,每人从中任意抽取3张,然后将牌面上的三个数相乘,结果较大者为胜.
(1)你认为抽取到哪三张牌时,不管对方抽到其他怎样的三张,你都会赢?
(2)你认为抽取到哪三张牌时,不管对方抽到其他怎样的三张,你都会输?
(3)结果等于6的可能性有几种?把每一种都写出来.
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】红
11.【答案】
12.【答案】A
13.【答案】解:
14.【答案】解:(1)所有可能结果如下:甲、乙、丙,甲、丙、乙,乙、甲、丙,乙、丙、甲,丙、甲、乙,丙、乙、甲,共6种.
(2)一样大.
理由如下:由(1)可知张先生乘坐到甲车有两种可能:乙、丙、甲,丙、乙、甲,
李先生乘坐到甲车有两种可能:甲、乙、丙,甲、丙、乙,
所以两人乘坐到甲车的可能性一样大.
15.【答案】解:(1)∵,
∴抽到4的可能性大;
(2))∵,
∴抽到偶数的可能性大;
(3)最小的五位数为:22233.
16.【答案】解:(1)y=-12x+12+2a=3(x-2)+2a,且3>0,
当x<2时,y随x的增大而减小.
x<0是x<2的一部分,
x<0时y随x的增大而减小,即A是必然事件.
(2)=-43(12+2a)=-24a,
当a>0时,-24a<0,此时二次函数y=-12x+12+2a的图象与x轴没有交点;
当a=0时,-24a=0,此时二次函数y= -12x+12+2a的图象与x轴只有一个交点;
当a<0时,-24a>0,此时二次函数y=-12x+12+2a的图象与x轴有两个交点.
故B是随机事件.
17.【答案】解:(1)由题意分析可得:要使他两次数字之和为100,则第二次必须转到95,
因为总共有20个数字,
所以他两次数字之和为100的可能性为;
(2)由题意分析可得:转到数字35以上就会“爆掉”,共有13种情况,
因为总共有20个数字,
所以“爆掉”的可能性为.
18.【答案】解:(1)当抽到 10, 9,10时,乘积为900,不管对方抽到其他怎样的三张,都会赢;
或抽到10, 9, 8时,乘积为720,不管对方抽到其他怎样的三张,都会赢;
(2)当抽到10,9, 10时,乘积为 900,不管对方抽到其他怎样的三张,都会输;
(3)结果等于6的可能性有5种:
1×2×3;
1×( 2)×3;
1×2×( 3);
1×( 2)×( 3);
1×( 1)×( 6).
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共27分)
下列事件中是不可能事件的是( )
A. 守株待兔 B. 瓮中捉鳖 C. 水中捞月 D. 百步穿杨
下列事件是必然事件的为( )
A. 任意一个五边形的外角和为
B. 抛掷一枚均匀的硬币次,正面朝上的次数为
C. 个人中至少有两个人的出生月份是相同的
D. 太阳从西方升起
两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3,从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )
A. 两个小球的标号之和等于 B. 两个小球的标号之和等于
C. 两个小球的标号之和大于 D. 两个小球的标号之和大于
某商贩设计了一个转盘游戏,游戏规则如下:
游戏规则
转动转盘,若指针停在偶数所在区域,则停止游戏;若指针停在奇数所在区域,则抽出一个弹珠,当弹珠为黑色时,得百元大奖,否则游戏结束.
转盘和袋子里的弹珠如图所示,某位游客想玩这个游戏,则他获得百元大奖的可能性( )
A. 为 B. 约为 C. 非常小 D. 约为
抛掷一枚质地均匀的硬币2000次,正面朝上的次数最有可能为( )
A. B. C. D.
在一个布袋中装有红、白两种颜色的球, 它们除颜色外没有任何其他区别, 其中红球若干,白球5个,袋中的球已搅匀,若从袋中随机取出一个球,取出红球的可能性大,则红球( )
A. 有个 B. 有个
C. 不足个 D. 有个或个以上
在某校艺体节的乒乓球比赛中,李东同学顺利进入总决赛,且个人技艺高超,有同学预测“李东夺冠的可能性是80%”,对该同学的说法理解正确的是( )
A. 李东夺冠的可能性较小
B. 李东和他的对手比赛局时,他一定赢局
C. 李东夺冠的可能性较大
D. 李东肯定会赢
如图,电路图上有4个开关A,B,C,D和1个小灯泡,同时闭合开关A,B或同时闭合开关C,D都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A. 只闭合个开关 B. 只闭合个开关
C. 只闭合个开关 D. 闭合个开关
如图所示的为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同, 经过四层净化后流入底部的5个出口中的一个.下列判断:
5个出口的出水量相同;
2号出口的出水量与4号出口的出水量相同;
1,2,3号出口的出水量之比约为1:4:6;
若净化材料损耗的速度与流经其表面的水量成正比,则更换最慢的一个三角形材料使用的时间约为更换最快的一个三角形材料使用时间的8倍.
其中正确的判断有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共3小题,共9分)
一个袋中装有6个红球,5个黄球,3个白球,每个球除颜色外都相同,任意摸出一球,摸到______球的可能性最大.
转动如图所示的可以自由转动的转盘,当转盘停止时,猜想指针落在黑色区域内的可能性大小,将转盘的序号按可能性从小到大的顺序排列为 .
在如图所示(A,B,C三个区域)的图形中随机撒一把豆子,豆子落在 区域的可能性最大.(填“A”“B”或“C”)
三、解答题(本大题共6小题,共64分)
下面第一排表示十张扑克牌的不同情况,任意摸一张,请你将摸到红色扑克牌的可能性与对应的方框用线连起来.
某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果.
(2)两人中,谁乘坐到甲车的可能性大 请说明理由.
有12张标有数字2,2,2,3,3,4,4,4,5,5,6,7的卡片,从中任意抽取一张.
(1)抽出的数字是4和5的可能性哪个大?
(2)抽出的数字是奇数和偶数的可能性哪个大?
(3)连续抽5次(抽出后不放回),抽出的五个数组成的五位数最小可能是多少?
已知关于x的二次函数y=-12x+12+2a,设事件A:“x<0时,y随x的增大而减小”,事件B:“二次函数y=-12x+12+2a的图象与x轴有两个交点”.
(1)小聪说A是必然事件,请你说明其中的道理;
(2)小明说B是随机事件,请你说明其中的道理.
某电视节目中有一个游戏环节是大转轮比赛,转轮上平均分布着5,10,15,20,…,95,100共20个数字.选手依次转动转轮,每个人有两次机会.选手中转动的数字之和最大且不超过100者胜出;若超过100则成绩无效,称为“爆掉”.
(1)某选手第一次转到了数字5,再转第二次,则两次数字之和为100的可能性有多大?
(2)现在某选手第一次转到了数字65,若再转第二次,则有可能“爆掉”,请你分析“爆掉”的可能性有多大.
甲、乙两人玩一种游戏:共20张牌,牌面上分别写有-10,-9,-8,…,-1,1,2,…,10,洗好牌后,将背面朝上,每人从中任意抽取3张,然后将牌面上的三个数相乘,结果较大者为胜.
(1)你认为抽取到哪三张牌时,不管对方抽到其他怎样的三张,你都会赢?
(2)你认为抽取到哪三张牌时,不管对方抽到其他怎样的三张,你都会输?
(3)结果等于6的可能性有几种?把每一种都写出来.
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】红
11.【答案】
12.【答案】A
13.【答案】解:
14.【答案】解:(1)所有可能结果如下:甲、乙、丙,甲、丙、乙,乙、甲、丙,乙、丙、甲,丙、甲、乙,丙、乙、甲,共6种.
(2)一样大.
理由如下:由(1)可知张先生乘坐到甲车有两种可能:乙、丙、甲,丙、乙、甲,
李先生乘坐到甲车有两种可能:甲、乙、丙,甲、丙、乙,
所以两人乘坐到甲车的可能性一样大.
15.【答案】解:(1)∵,
∴抽到4的可能性大;
(2))∵,
∴抽到偶数的可能性大;
(3)最小的五位数为:22233.
16.【答案】解:(1)y=-12x+12+2a=3(x-2)+2a,且3>0,
当x<2时,y随x的增大而减小.
x<0是x<2的一部分,
x<0时y随x的增大而减小,即A是必然事件.
(2)=-43(12+2a)=-24a,
当a>0时,-24a<0,此时二次函数y=-12x+12+2a的图象与x轴没有交点;
当a=0时,-24a=0,此时二次函数y= -12x+12+2a的图象与x轴只有一个交点;
当a<0时,-24a>0,此时二次函数y=-12x+12+2a的图象与x轴有两个交点.
故B是随机事件.
17.【答案】解:(1)由题意分析可得:要使他两次数字之和为100,则第二次必须转到95,
因为总共有20个数字,
所以他两次数字之和为100的可能性为;
(2)由题意分析可得:转到数字35以上就会“爆掉”,共有13种情况,
因为总共有20个数字,
所以“爆掉”的可能性为.
18.【答案】解:(1)当抽到 10, 9,10时,乘积为900,不管对方抽到其他怎样的三张,都会赢;
或抽到10, 9, 8时,乘积为720,不管对方抽到其他怎样的三张,都会赢;
(2)当抽到10,9, 10时,乘积为 900,不管对方抽到其他怎样的三张,都会输;
(3)结果等于6的可能性有5种:
1×2×3;
1×( 2)×3;
1×2×( 3);
1×( 2)×( 3);
1×( 1)×( 6).
第1页,共1页
同课章节目录
