河北省部分重点学校2022届高三上学期期中考试数学试卷(扫描版含答案解析)
文档属性
| 名称 | 河北省部分重点学校2022届高三上学期期中考试数学试卷(扫描版含答案解析) | 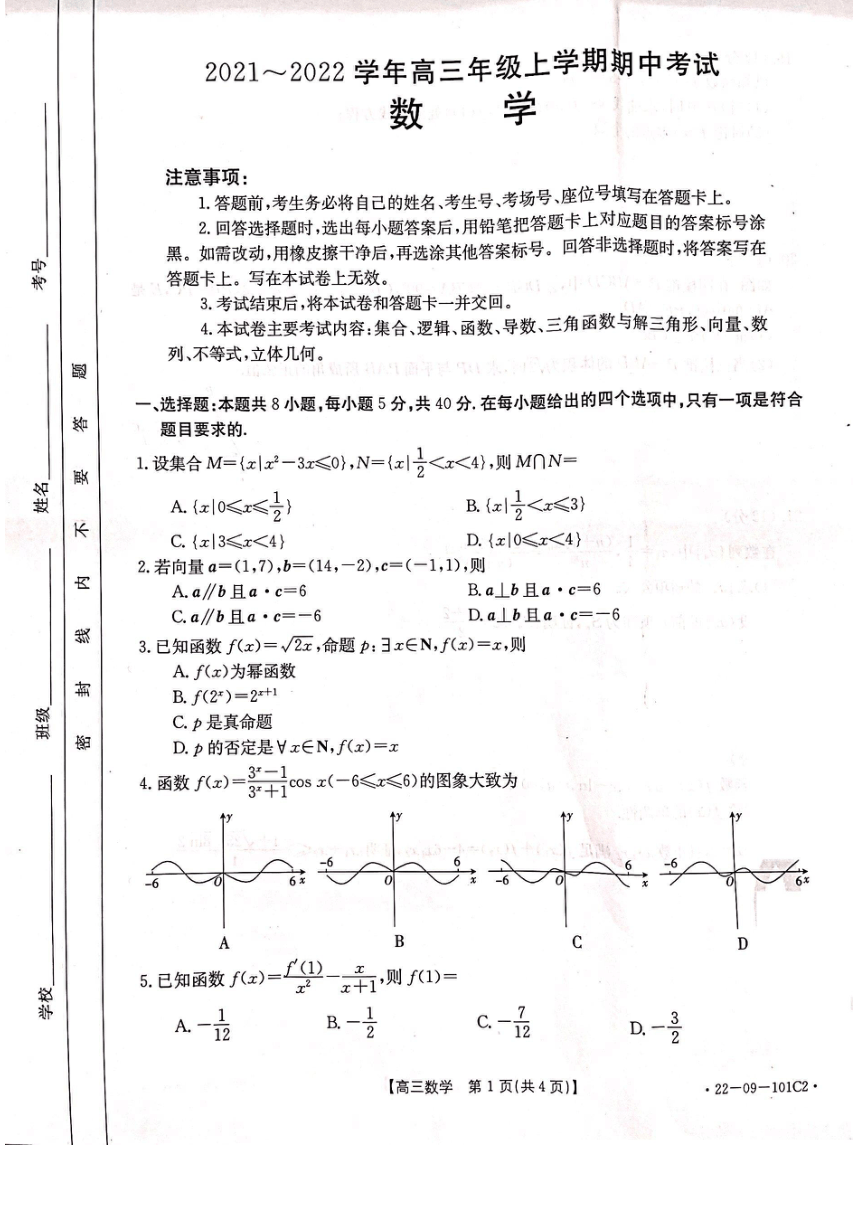 | |
| 格式 | |||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 13:43:39 | ||
图片预览




文档简介
2021~2022学年高三年级上学期期中考试
数学
注意事项:
1.答题前,考生务必将自己的姓名考生号考场号座位号填写在答题卡上
2回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在
答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回
4.本试卷主要考试内容:集合、逻辑、函数导数、三角函数与解三角形、向量数
列、不等式,立体几何。
选择题本题共8小题,每小题5分,共40分,在每小题给出的四个选项中只有一项是符合
题目要求的
1.设集合M={x|x2-3x≤0},N={x敦
B.{xl2K
C.{x|3≤x<
D.{x10≤x<4}
2.若向量a=(1,7),b=(14,-2),c=(-1,1),则
A.a∥b且
B.a⊥b且a·c=6
C.a∥b且a·c=-6
D.a⊥b且a·c=-6
3已知函数f()=√a,命题p:∈EN,(m)=x,则
A.f(x)为幂函数
B.f(2x)=2+1
C.p是真命题
D.p的否定是x∈N,f(x)=x
4函数f(2)=3118x(-6≤x≤6)的图象大致为
B
C
D
5已知函数f(x)=C(1)_x
+1,则f(1)
B
7
D
高三数学第1页(共4页
22-09-101C2
6.函数f(x)=sin(x-2x)+3cos(-2x)图象的对称中心的坐标为
A
0)(k∈Z
B.(x+,0)(k∈Z)
丌⊥是丌
0)(k∈Z
D.(
0)(k∈Z
7.在三棱锥P一ABC中PC⊥平面ABC,PA=PB=5,AC=BC=3,AB=2√5,则二面角
AB-C的正切值为
A.2
82021年小林大学毕业后,9月1日开始工作,他决定给自已开一张储蓄银行卡,每月的10号
存钱至该银行卡(假设当天存钱次日到账)2021年9月10日他在卡上存入1元,以后每月
存的钱数比上个月多一倍,则他这张银行卡账上存钱总额(不含银行利息)首次达到1万元的
时间为
A.2022年12月11日
B.2022年11月11日
C.2022年10月11日
D.2022年9月11日
选择题:本题共4小题,每小题5分,共20分在每小题给出的选项中,有多项符合题目要
求全部选对的得5分,部分选对的得2分,有选错的得0分
9.已知角a的终边经过点(-1,2),则
B tan
1+√5
sin acos a 9
C tan(r-2a=-4
D.若a为钝角,则
10.在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱
A1D1,A1B1,B1C1,C1D1的中点,将该正方体挖去两个大小完全相同
的四分之一圆锥,得到如图所示的几何体,则
CG∥平面ADE
B.该几何体的上底面的周长为4+π
C.该几何体的的体积为
D.三棱锥F一ABC的外接球的表面积为1x
已知x>y>1,则
A.(x+1)(2+4)的最小值为9
x2>3x-1”是“y>3”的必要不充分条件
C xt
4(x-1+y)
的最小值为9
D.“x>y2”是“x>y+2”的充分不必要条件
12已知a=lg3,函数f()=+lx-4的零点为b,g(x)=x2-x2-z的极小值点
为c,则
A, a>b
B c>b
Cb>a
D. b>e
【高三数学第2页(共4页)
22-09-101C2
数学
注意事项:
1.答题前,考生务必将自己的姓名考生号考场号座位号填写在答题卡上
2回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在
答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回
4.本试卷主要考试内容:集合、逻辑、函数导数、三角函数与解三角形、向量数
列、不等式,立体几何。
选择题本题共8小题,每小题5分,共40分,在每小题给出的四个选项中只有一项是符合
题目要求的
1.设集合M={x|x2-3x≤0},N={x
B.{xl2
C.{x|3≤x<
D.{x10≤x<4}
2.若向量a=(1,7),b=(14,-2),c=(-1,1),则
A.a∥b且
B.a⊥b且a·c=6
C.a∥b且a·c=-6
D.a⊥b且a·c=-6
3已知函数f()=√a,命题p:∈EN,(m)=x,则
A.f(x)为幂函数
B.f(2x)=2+1
C.p是真命题
D.p的否定是x∈N,f(x)=x
4函数f(2)=3118x(-6≤x≤6)的图象大致为
B
C
D
5已知函数f(x)=C(1)_x
+1,则f(1)
B
7
D
高三数学第1页(共4页
22-09-101C2
6.函数f(x)=sin(x-2x)+3cos(-2x)图象的对称中心的坐标为
A
0)(k∈Z
B.(x+,0)(k∈Z)
丌⊥是丌
0)(k∈Z
D.(
0)(k∈Z
7.在三棱锥P一ABC中PC⊥平面ABC,PA=PB=5,AC=BC=3,AB=2√5,则二面角
AB-C的正切值为
A.2
82021年小林大学毕业后,9月1日开始工作,他决定给自已开一张储蓄银行卡,每月的10号
存钱至该银行卡(假设当天存钱次日到账)2021年9月10日他在卡上存入1元,以后每月
存的钱数比上个月多一倍,则他这张银行卡账上存钱总额(不含银行利息)首次达到1万元的
时间为
A.2022年12月11日
B.2022年11月11日
C.2022年10月11日
D.2022年9月11日
选择题:本题共4小题,每小题5分,共20分在每小题给出的选项中,有多项符合题目要
求全部选对的得5分,部分选对的得2分,有选错的得0分
9.已知角a的终边经过点(-1,2),则
B tan
1+√5
sin acos a 9
C tan(r-2a=-4
D.若a为钝角,则
10.在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱
A1D1,A1B1,B1C1,C1D1的中点,将该正方体挖去两个大小完全相同
的四分之一圆锥,得到如图所示的几何体,则
CG∥平面ADE
B.该几何体的上底面的周长为4+π
C.该几何体的的体积为
D.三棱锥F一ABC的外接球的表面积为1x
已知x>y>1,则
A.(x+1)(2+4)的最小值为9
x2>3x-1”是“y>3”的必要不充分条件
C xt
4(x-1+y)
的最小值为9
D.“x>y2”是“x>y+2”的充分不必要条件
12已知a=lg3,函数f()=+lx-4的零点为b,g(x)=x2-x2-z的极小值点
为c,则
A, a>b
B c>b
Cb>a
D. b>e
【高三数学第2页(共4页)
22-09-101C2
同课章节目录
