河南省三门峡市渑池县高级中学2021-2022学年高一上学期期中考试数学试卷(Word版含答案)
文档属性
| 名称 | 河南省三门峡市渑池县高级中学2021-2022学年高一上学期期中考试数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 395.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 13:48:56 | ||
图片预览




文档简介
渑池县高级中学2021-2022学年高一上学期期中考试
数学试卷
一、单选题
1.设向量 , ,且 ,则 =( ).
A. B. C. D.
2.已知全集 , , ,则集合 ( )
A. B. C. D.
3.已知向量 (k,6), (﹣2,3),且 ⊥ ,则k的值是( )
A. ﹣4 B. ﹣3 C. 4 D. 9
4.已知 , , ,则实数 ( )
A. B. C. 8 D. -4
5.等差数列 公差为 ,且满足 , , 成等比数列,则 ( )
A.
B.0或
C.2
D.0或2
6.命题“ , ”的否定是( )
A. , B. , C. , D. ,
7.已知角α终边上一点M的坐标为 ,则 ( )
A. B. C. D.
8.已知全集 ,集合 , ,则 为( )
A. B. {4} C. D.
9.若 则 在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
10.下列推理错误的是( )
A. B. ,
C. , D.
11.已知函数 是 上的增函数, , 是其图象上的两点,那么 的解集是( )
A. B. C. D.
12.已知向量 、 ,其中 , ,且 ,则向量 和 的夹角是( )
A. B. C. D.
13.当 时,下列函数最小值为2的是( )
A. B. C. D.
14.已知 ,则下列 与 表示同一个函数的是( )
A. , B. ,
C. , D. ,
15.设 ,则( )
A. B. C. D.
16.已知函数是 上偶函数,且对于 都有 成立,当 , ,且 时,都有 .对于下列叙述;
① ;
②直线 是函数 的一条对称轴;
③函数 在区间 上为增函数;
④函数 在区间 上有四个零点.其中正确命题的序号是( )
A. ①②③ B. ①② C. ②④ D. ①②④
17.若函数 的值域为 ,则实数 的取值范围是( )
A. B. C. D.
18.以 为圆心, 为半径的圆的方程为( )
A. B.
C. D.
19.如果 的三个内角的正弦值分别等于 的三个内角的余弦值,则下列正确的是( )
A. 与 都是锐角三角形 B. 与 都是钝角三角形
C. 是锐角三角形且 是钝角三角形 D. 是钝角三角形且 是锐角三角形
20.已知函数y=f(x+1)定义域是[-2,5],则y=f(3x-1)的定义域是( )
A. [-10,13] B. [-1,4] C. [0, ] D. [-1, ]
二、填空题
21.已知函数 ( ,且 )的图象过定点P,且点P在幂函数 的图象上,则 .
22.在平行四边形ABCD中,AD=1,AB=2,∠BAD=60°,E是CD的中点,则 =________.
23.数列{an}满足 ,且 ,则a2017=________.
24.________.
25.已知点P为线段y=2x,x∈[2,4]上任意一点,点Q为圆C:(x﹣3)2+(y+2)2=1上一动点,则线段|PQ|的最小值为
26.已知偶函数 在区间 上单调递增,则满足 的x的取值范围是________.
27.若函数f(x)=3sin(2x﹣ )的图象为C,则下列结论中正确的序号是________. ①图象C关于直线x= 对称;
②图象C关于点( ,0)对称;
③函数f(x)在区间(﹣ , )内不是单调的函数;
④由y=3sin2x的图象向右平移 个单位长度可以得到图象C.
28.已知函数 , ,若对任意 ,总存在 ,使得 ,则实数 的取值范围是
29.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣x2 , 若存在实数a,b,使f(x)在[a,b]上的值域为[ , ],则ab=________.
30.下列说法中,正确的有 . (写出所有正确说法的序号)
①已知关于x的不等式mx2+mx+2>0的角集为R,则实数m的取值范围是0<m<4.
②已知等比数列{an}的前n项和为Sn , 则Sn、S2n﹣Sn、S3n﹣S2n也构成等比数列.
③已知函数 (其中a>0且a≠1)在R上单调递减,且关于x的方程 恰有两个不相等的实数解,则 .
④已知a>0,b>﹣1,且a+b=1,则 + 的最小值为 .
⑤在平面直角坐标系中,O为坐标原点,| |=| |=| |=1, + + = ,A(1,1),则 的取值范围是 .
三、解答题
31.一个总体中的1 000个个体编号为0,1,2,…,999,并依次将其分为10个小组,组号为0,1,2,…,9.要用系统抽样方法抽取一个容量为10的样本,规定如果在第0组随机抽取的号码为x,那么依次错位地得到后面各组的号码,即第k组中抽取的号码的后两位数为x+33k的后两位数.
(1).当x=24时,写出所抽取样本的10个号码;
(2).若所抽取样本的10个号码中有一个的后两位数是87,求x的取值范围.
32.已知 , .
(1)求 , ;
(2)求 的值.
33.已知函数 ,其中 ,且 .
(1)求 的定义域;
(2)求 的零点;
(3)比较 与 的大小
34.已知 .
(Ⅰ)求 的值;
(Ⅱ)求 的值.
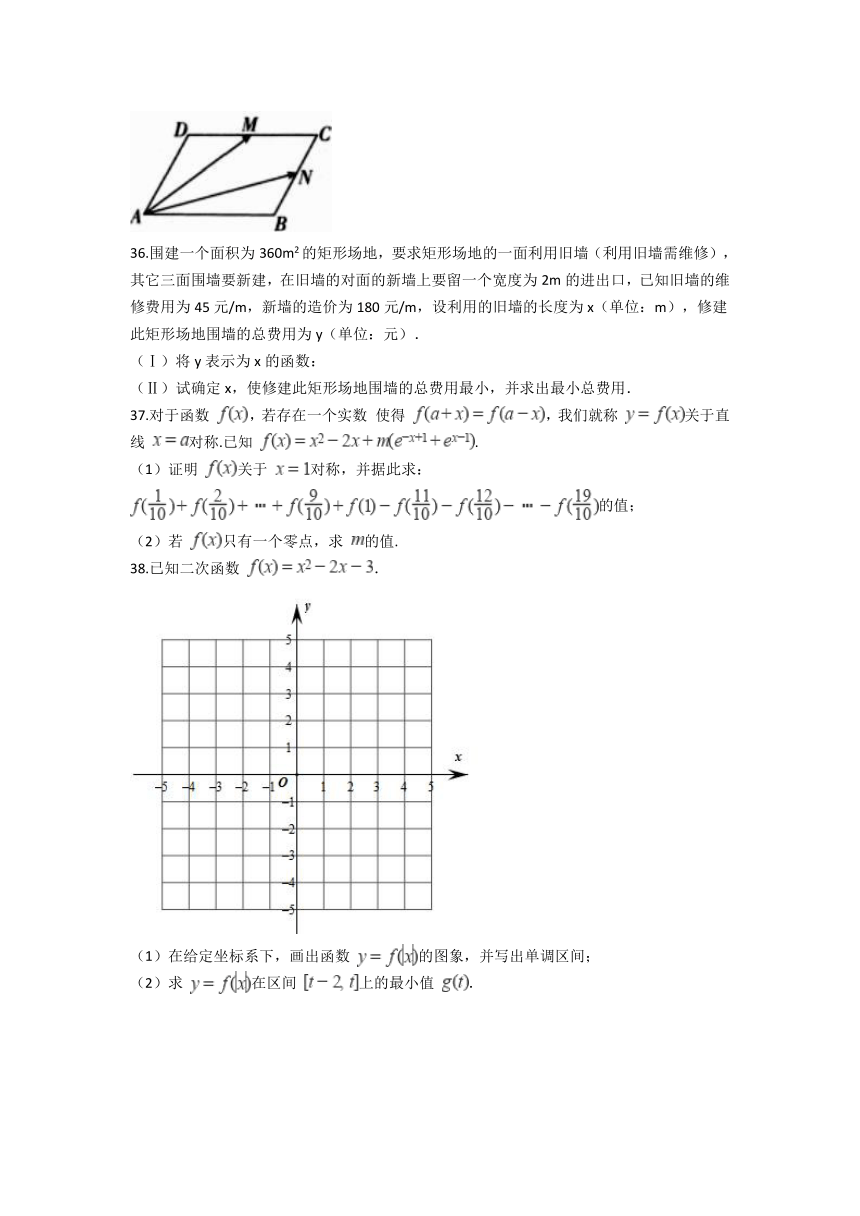
35.如图所示,在平行四边形 中, , 分别为 , 的中点,已知 ,试用 表示 .
36.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
37.对于函数 ,若存在一个实数 使得 ,我们就称 关于直线 对称.已知 .
(1)证明 关于 对称,并据此求: 的值;
(2)若 只有一个零点,求 的值.
38.已知二次函数 .
(1)在给定坐标系下,画出函数 的图象,并写出单调区间;
(2)求 在区间 上的最小值 .
答案
一、单选题
1.【答案】 A
2.【答案】 C
3.【答案】 D
4.【答案】 C
5.【答案】 B
6.【答案】 D
7.【答案】 D
8.【答案】 D
9.【答案】 D
10.【答案】 D
11.【答案】 B
12.【答案】 A
13.【答案】 B
14.【答案】 C
15.【答案】 C
16.【答案】 D
17.【答案】 A
18.【答案】 C
19.【答案】 D
20.【答案】 C
二、填空题
21.【答案】 3
22.【答案】﹣
23.【答案】
24.【答案】
25.【答案】 ﹣1
26.【答案】 (-3.3)
27.【答案】①②
28.【答案】 或
29.【答案】
30.【答案】 ④⑤
三、解答题
31.【答案】 (1)解:当x=24时,按规则可知所抽取样本的10个号码依次为:
24,157,290,323,456,589,622,755,888,921
(2)解:当k=0,1,2,…,9时,33k的值依次为:
0,33,66,99,132,165,198,231,264,297.
又抽取样本的10个号码中有一个的后两位数是87,从而x可以为:
87,54,21,88,55,22,89,56,23,90.
∴x的取值范围是{21,22,23,54,55,56,87,88,89,90}
32.【答案】 (1)解: , , ,
(2)解:
.
33.【答案】 (1)解:由 ,得 ,
所以函数 的定义域为 .
(2)解:令 ,即 ,
则 ,所以 ,
所以函数 的零点为2.
(3)解: ,
,
当 时,函数 是增函数,所以 ,即 .
当 时,函数 是减函数,所以 ,即 .
34.【答案】 解:(Ⅰ)∵ ,
∴
(Ⅱ)原式
35.【答案】 解: ,
解得
所以 ,
36.【答案】 解:(Ⅰ)设矩形的另一边长为am,
则y=45x+180(x﹣2)+180 2a=225x+360a﹣360.
由已知ax=360,得 ,
所以 .
(II)因为x>0,所以 ,
所以 ,当且仅当 时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
37.【答案】 (1)解:
又
∴ ,
∴函数 的图象关于 对称。
由题意知
(2)解:由(1)知 关于 对称,且 只有一个零点,
则这个零点一定就是 ,
,
解得
当 时,
时, 时,
故当 时函数只有一个零点,符合题意.
∴ 。
38.【答案】 (1)解:函数 的图象如下:
由图可知,单调递增区间为 和 ,单调递减区间为 和
(2)解: ,
当 时, 在 单调递减,
故 ;
当 时, ;
当 时,即 时,
在 在 上单调递增, ,
故
数学试卷
一、单选题
1.设向量 , ,且 ,则 =( ).
A. B. C. D.
2.已知全集 , , ,则集合 ( )
A. B. C. D.
3.已知向量 (k,6), (﹣2,3),且 ⊥ ,则k的值是( )
A. ﹣4 B. ﹣3 C. 4 D. 9
4.已知 , , ,则实数 ( )
A. B. C. 8 D. -4
5.等差数列 公差为 ,且满足 , , 成等比数列,则 ( )
A.
B.0或
C.2
D.0或2
6.命题“ , ”的否定是( )
A. , B. , C. , D. ,
7.已知角α终边上一点M的坐标为 ,则 ( )
A. B. C. D.
8.已知全集 ,集合 , ,则 为( )
A. B. {4} C. D.
9.若 则 在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
10.下列推理错误的是( )
A. B. ,
C. , D.
11.已知函数 是 上的增函数, , 是其图象上的两点,那么 的解集是( )
A. B. C. D.
12.已知向量 、 ,其中 , ,且 ,则向量 和 的夹角是( )
A. B. C. D.
13.当 时,下列函数最小值为2的是( )
A. B. C. D.
14.已知 ,则下列 与 表示同一个函数的是( )
A. , B. ,
C. , D. ,
15.设 ,则( )
A. B. C. D.
16.已知函数是 上偶函数,且对于 都有 成立,当 , ,且 时,都有 .对于下列叙述;
① ;
②直线 是函数 的一条对称轴;
③函数 在区间 上为增函数;
④函数 在区间 上有四个零点.其中正确命题的序号是( )
A. ①②③ B. ①② C. ②④ D. ①②④
17.若函数 的值域为 ,则实数 的取值范围是( )
A. B. C. D.
18.以 为圆心, 为半径的圆的方程为( )
A. B.
C. D.
19.如果 的三个内角的正弦值分别等于 的三个内角的余弦值,则下列正确的是( )
A. 与 都是锐角三角形 B. 与 都是钝角三角形
C. 是锐角三角形且 是钝角三角形 D. 是钝角三角形且 是锐角三角形
20.已知函数y=f(x+1)定义域是[-2,5],则y=f(3x-1)的定义域是( )
A. [-10,13] B. [-1,4] C. [0, ] D. [-1, ]
二、填空题
21.已知函数 ( ,且 )的图象过定点P,且点P在幂函数 的图象上,则 .
22.在平行四边形ABCD中,AD=1,AB=2,∠BAD=60°,E是CD的中点,则 =________.
23.数列{an}满足 ,且 ,则a2017=________.
24.________.
25.已知点P为线段y=2x,x∈[2,4]上任意一点,点Q为圆C:(x﹣3)2+(y+2)2=1上一动点,则线段|PQ|的最小值为
26.已知偶函数 在区间 上单调递增,则满足 的x的取值范围是________.
27.若函数f(x)=3sin(2x﹣ )的图象为C,则下列结论中正确的序号是________. ①图象C关于直线x= 对称;
②图象C关于点( ,0)对称;
③函数f(x)在区间(﹣ , )内不是单调的函数;
④由y=3sin2x的图象向右平移 个单位长度可以得到图象C.
28.已知函数 , ,若对任意 ,总存在 ,使得 ,则实数 的取值范围是
29.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣x2 , 若存在实数a,b,使f(x)在[a,b]上的值域为[ , ],则ab=________.
30.下列说法中,正确的有 . (写出所有正确说法的序号)
①已知关于x的不等式mx2+mx+2>0的角集为R,则实数m的取值范围是0<m<4.
②已知等比数列{an}的前n项和为Sn , 则Sn、S2n﹣Sn、S3n﹣S2n也构成等比数列.
③已知函数 (其中a>0且a≠1)在R上单调递减,且关于x的方程 恰有两个不相等的实数解,则 .
④已知a>0,b>﹣1,且a+b=1,则 + 的最小值为 .
⑤在平面直角坐标系中,O为坐标原点,| |=| |=| |=1, + + = ,A(1,1),则 的取值范围是 .
三、解答题
31.一个总体中的1 000个个体编号为0,1,2,…,999,并依次将其分为10个小组,组号为0,1,2,…,9.要用系统抽样方法抽取一个容量为10的样本,规定如果在第0组随机抽取的号码为x,那么依次错位地得到后面各组的号码,即第k组中抽取的号码的后两位数为x+33k的后两位数.
(1).当x=24时,写出所抽取样本的10个号码;
(2).若所抽取样本的10个号码中有一个的后两位数是87,求x的取值范围.
32.已知 , .
(1)求 , ;
(2)求 的值.
33.已知函数 ,其中 ,且 .
(1)求 的定义域;
(2)求 的零点;
(3)比较 与 的大小
34.已知 .
(Ⅰ)求 的值;
(Ⅱ)求 的值.
35.如图所示,在平行四边形 中, , 分别为 , 的中点,已知 ,试用 表示 .
36.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
37.对于函数 ,若存在一个实数 使得 ,我们就称 关于直线 对称.已知 .
(1)证明 关于 对称,并据此求: 的值;
(2)若 只有一个零点,求 的值.
38.已知二次函数 .
(1)在给定坐标系下,画出函数 的图象,并写出单调区间;
(2)求 在区间 上的最小值 .
答案
一、单选题
1.【答案】 A
2.【答案】 C
3.【答案】 D
4.【答案】 C
5.【答案】 B
6.【答案】 D
7.【答案】 D
8.【答案】 D
9.【答案】 D
10.【答案】 D
11.【答案】 B
12.【答案】 A
13.【答案】 B
14.【答案】 C
15.【答案】 C
16.【答案】 D
17.【答案】 A
18.【答案】 C
19.【答案】 D
20.【答案】 C
二、填空题
21.【答案】 3
22.【答案】﹣
23.【答案】
24.【答案】
25.【答案】 ﹣1
26.【答案】 (-3.3)
27.【答案】①②
28.【答案】 或
29.【答案】
30.【答案】 ④⑤
三、解答题
31.【答案】 (1)解:当x=24时,按规则可知所抽取样本的10个号码依次为:
24,157,290,323,456,589,622,755,888,921
(2)解:当k=0,1,2,…,9时,33k的值依次为:
0,33,66,99,132,165,198,231,264,297.
又抽取样本的10个号码中有一个的后两位数是87,从而x可以为:
87,54,21,88,55,22,89,56,23,90.
∴x的取值范围是{21,22,23,54,55,56,87,88,89,90}
32.【答案】 (1)解: , , ,
(2)解:
.
33.【答案】 (1)解:由 ,得 ,
所以函数 的定义域为 .
(2)解:令 ,即 ,
则 ,所以 ,
所以函数 的零点为2.
(3)解: ,
,
当 时,函数 是增函数,所以 ,即 .
当 时,函数 是减函数,所以 ,即 .
34.【答案】 解:(Ⅰ)∵ ,
∴
(Ⅱ)原式
35.【答案】 解: ,
解得
所以 ,
36.【答案】 解:(Ⅰ)设矩形的另一边长为am,
则y=45x+180(x﹣2)+180 2a=225x+360a﹣360.
由已知ax=360,得 ,
所以 .
(II)因为x>0,所以 ,
所以 ,当且仅当 时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
37.【答案】 (1)解:
又
∴ ,
∴函数 的图象关于 对称。
由题意知
(2)解:由(1)知 关于 对称,且 只有一个零点,
则这个零点一定就是 ,
,
解得
当 时,
时, 时,
故当 时函数只有一个零点,符合题意.
∴ 。
38.【答案】 (1)解:函数 的图象如下:
由图可知,单调递增区间为 和 ,单调递减区间为 和
(2)解: ,
当 时, 在 单调递减,
故 ;
当 时, ;
当 时,即 时,
在 在 上单调递增, ,
故
同课章节目录
