26.1.1反比例函数 课件(共18张PPT)
文档属性
| 名称 | 26.1.1反比例函数 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
26.1.1反比例函数
人教版 九年级下册
学习目标
1.了解反比例函数的概念,能判断一个给定的函数是否为反比例函数.
2.会用待定系数法求反比例函数解析式. (重点)
3.能根据实际问题中的条件确定反比例函数的解析式. (重点、难点)
复习回顾
我们已经学习过的函数有哪些?
1.一次函数。
2.正比例函数。
一般地,形如y=kx+b(k,b是常数, k≠0)的函数,叫做一次函数。
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数。
3.二次函数。
一般地,形如y= (a,b,c是常数,a≠0)的函数,叫做二次函数。
新知导入
在生活中,我们都看到过棉花和铁,我们知道同样重的棉花和铁块,棉花明明看着更多,它的密度反而更小,你认同吗?为什么?
探究新知
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
(1) 某小区的游泳池的容量是80m3,现在要把游泳池里面的水放干,已知每小时的放水量是x(单位:m3 ),随着水池里面的水逐渐放干,放水的时间t (单位:h) 和放水的速度x(单位:m3 )的变化关系;
(2) 某住宅小区要种植一块面积为 1000 m2 的矩形草坪,草坪的长 y (单位:m) 随宽 x (单位:m)的变化而变化;
(3) 已知北京市的总面积为1.68×104 km2 ,人均占有面积 S (单位:km2/人) 随全市总人口 n (单位:人) 的变化而变化.
探究新知
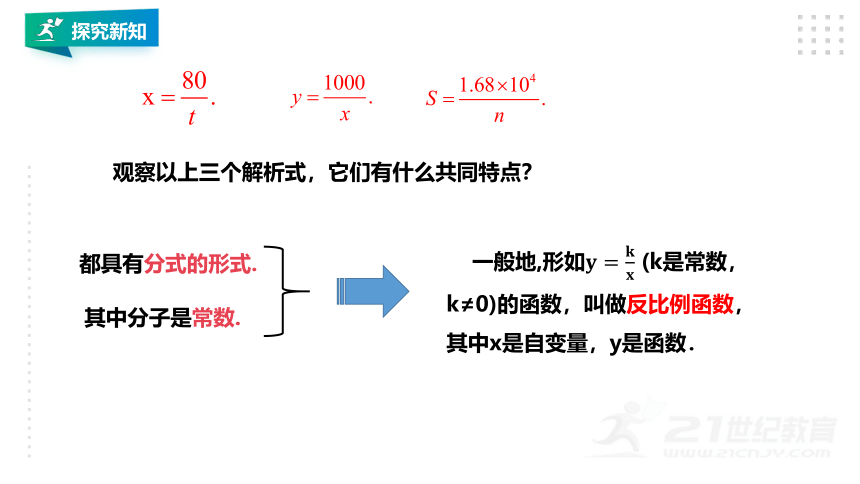
观察以上三个解析式,它们有什么共同特点?
都具有分式的形式.
其中分子是常数.
一般地,形如 (k是常数,k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
新课讲解
反比例函数的三种表达方式:(注意 k ≠ 0)
思考1:反比例函数 (k≠0) 的自变量 x 的取值范围是什么?
因为 x 作为分母,不能等于零,因此自变量 x 的取值范围是所有非零实数. 但实际问题中,应根据具体情况来确定反比例函数自变量的取值范围.
思考2:形如 的式子是反比例函数吗?
式子 呢?
试一试
下列函数中哪些是反比例函数,并指出相应k的值?
① y =3x-1 ② y =2x2 ③
不是
不是
是,k = 3
是,
④
典例精析
例1 已知 y 是 x 的反比例函数,并且当 x = 2 时, y = 6.
(1)写出 y 关于 x 的函数解析式;
(2)当 x = 4 时,求 y 的值.
解:(1)设 ,因为当 x = 2时,y = 6,所以有
解得 k = 12.
因此
(2)把 x =4代入 ,得
归纳总结
用待定系数法求反比例函数解析式的一般步骤:
①设出含有待定系数的反比例函数解析式,
②将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;
③解方程,求出待定系数;
④写出反比例函数解析式.
课堂练习
1. 下列函数不是反比例函数的是( )
A.y=﹣ B.y=
C. D.xy=1
A
2若函数是反比例函数,则m的值是( )
A.1 B.﹣2 C.2或﹣2 D.2
B
课堂练习
3.若函数y=是关于x的反比例函数,则a满足的条件是 .
a≠﹣3
4.下表中,如果a和b成正比例,x应填 ,如果a和b成反比例,x应填 .
25
9
a 3 5
b 15 x
课堂练习
5.写出下列问题中y与x之间的函数关系式,并判断是否为反比例函数.
(1)三角形的面积为36cm2,其底边长为ycm,该边上的高为xcm;
(2)圆锥的体积为60cm3,它的高为ycm,底面面积为xcm2.
解:(1)根据题意得:xy=36,
∴y=,
∴是反比例函数;
(2)由题意得:xy=60,
∴y=,
∴是反比例函数.
课后练习
1.下列函数中,是反比例函数的是( )
A.y= B.y= C.y=2x+1 D.2y=x
2.已知函数y=()是反比例函数,
则k的值为 .
3.美美用300元钱全部用来买营养品送给她妈妈,写出她所能购买营养品的数量y(kg)与单价x(元/kg)之间的关系式.问y是x的函数吗?y是x的反比例函数吗?
板书设计
用待定系数法求反比例函数解析式
反比例函数
反比例函数
定义
三种表达方式
作业布置
1.课后习题1-3题;
2.完成练习册本课时的习题。
https://www.21cnjy.com/help/help_extract.php
26.1.1反比例函数
人教版 九年级下册
学习目标
1.了解反比例函数的概念,能判断一个给定的函数是否为反比例函数.
2.会用待定系数法求反比例函数解析式. (重点)
3.能根据实际问题中的条件确定反比例函数的解析式. (重点、难点)
复习回顾
我们已经学习过的函数有哪些?
1.一次函数。
2.正比例函数。
一般地,形如y=kx+b(k,b是常数, k≠0)的函数,叫做一次函数。
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数。
3.二次函数。
一般地,形如y= (a,b,c是常数,a≠0)的函数,叫做二次函数。
新知导入
在生活中,我们都看到过棉花和铁,我们知道同样重的棉花和铁块,棉花明明看着更多,它的密度反而更小,你认同吗?为什么?
探究新知
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
(1) 某小区的游泳池的容量是80m3,现在要把游泳池里面的水放干,已知每小时的放水量是x(单位:m3 ),随着水池里面的水逐渐放干,放水的时间t (单位:h) 和放水的速度x(单位:m3 )的变化关系;
(2) 某住宅小区要种植一块面积为 1000 m2 的矩形草坪,草坪的长 y (单位:m) 随宽 x (单位:m)的变化而变化;
(3) 已知北京市的总面积为1.68×104 km2 ,人均占有面积 S (单位:km2/人) 随全市总人口 n (单位:人) 的变化而变化.
探究新知
观察以上三个解析式,它们有什么共同特点?
都具有分式的形式.
其中分子是常数.
一般地,形如 (k是常数,k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
新课讲解
反比例函数的三种表达方式:(注意 k ≠ 0)
思考1:反比例函数 (k≠0) 的自变量 x 的取值范围是什么?
因为 x 作为分母,不能等于零,因此自变量 x 的取值范围是所有非零实数. 但实际问题中,应根据具体情况来确定反比例函数自变量的取值范围.
思考2:形如 的式子是反比例函数吗?
式子 呢?
试一试
下列函数中哪些是反比例函数,并指出相应k的值?
① y =3x-1 ② y =2x2 ③
不是
不是
是,k = 3
是,
④
典例精析
例1 已知 y 是 x 的反比例函数,并且当 x = 2 时, y = 6.
(1)写出 y 关于 x 的函数解析式;
(2)当 x = 4 时,求 y 的值.
解:(1)设 ,因为当 x = 2时,y = 6,所以有
解得 k = 12.
因此
(2)把 x =4代入 ,得
归纳总结
用待定系数法求反比例函数解析式的一般步骤:
①设出含有待定系数的反比例函数解析式,
②将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;
③解方程,求出待定系数;
④写出反比例函数解析式.
课堂练习
1. 下列函数不是反比例函数的是( )
A.y=﹣ B.y=
C. D.xy=1
A
2若函数是反比例函数,则m的值是( )
A.1 B.﹣2 C.2或﹣2 D.2
B
课堂练习
3.若函数y=是关于x的反比例函数,则a满足的条件是 .
a≠﹣3
4.下表中,如果a和b成正比例,x应填 ,如果a和b成反比例,x应填 .
25
9
a 3 5
b 15 x
课堂练习
5.写出下列问题中y与x之间的函数关系式,并判断是否为反比例函数.
(1)三角形的面积为36cm2,其底边长为ycm,该边上的高为xcm;
(2)圆锥的体积为60cm3,它的高为ycm,底面面积为xcm2.
解:(1)根据题意得:xy=36,
∴y=,
∴是反比例函数;
(2)由题意得:xy=60,
∴y=,
∴是反比例函数.
课后练习
1.下列函数中,是反比例函数的是( )
A.y= B.y= C.y=2x+1 D.2y=x
2.已知函数y=()是反比例函数,
则k的值为 .
3.美美用300元钱全部用来买营养品送给她妈妈,写出她所能购买营养品的数量y(kg)与单价x(元/kg)之间的关系式.问y是x的函数吗?y是x的反比例函数吗?
板书设计
用待定系数法求反比例函数解析式
反比例函数
反比例函数
定义
三种表达方式
作业布置
1.课后习题1-3题;
2.完成练习册本课时的习题。
https://www.21cnjy.com/help/help_extract.php
