2021—2022学年北师大版九年级数学上册2.6 应用一元二次方程 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版九年级数学上册2.6 应用一元二次方程 同步测试卷(Word版含答案) | 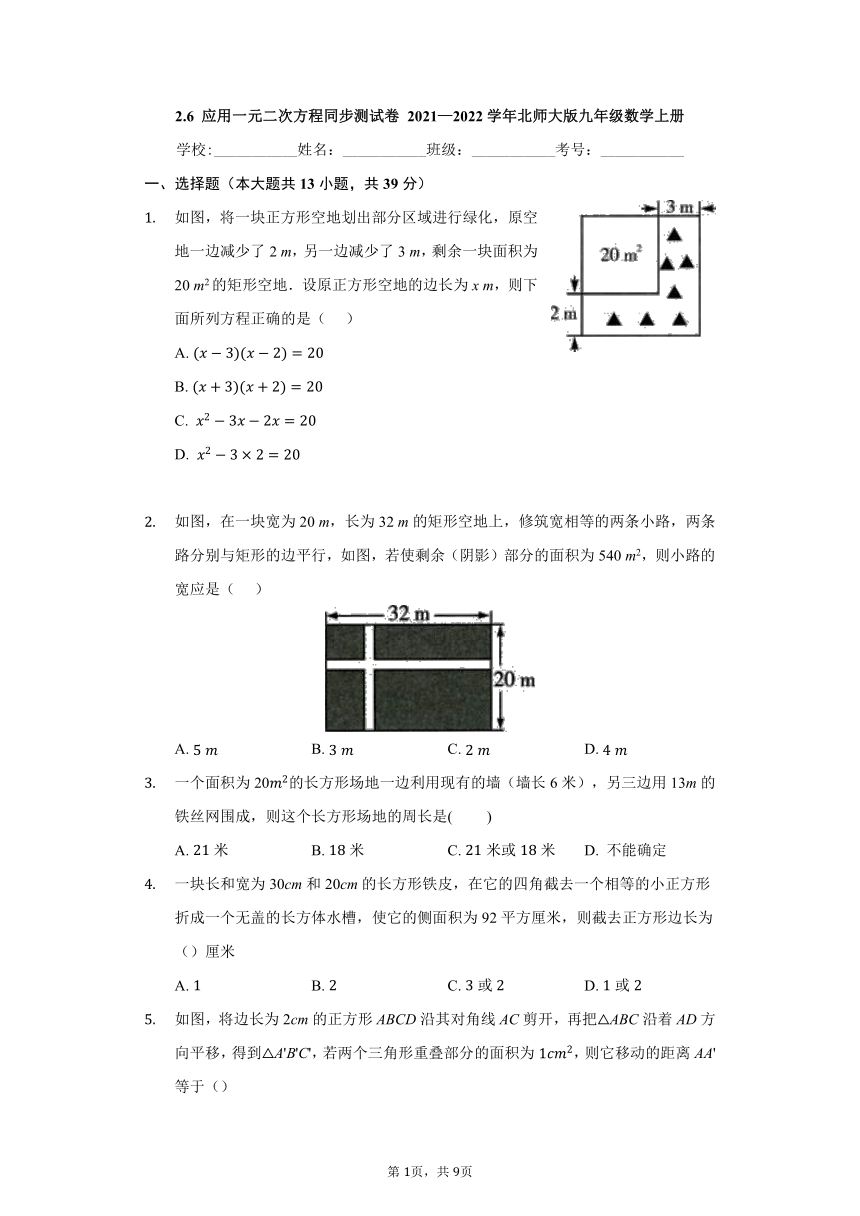 | |
| 格式 | docx | ||
| 文件大小 | 82.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 14:08:43 | ||
图片预览




文档简介
2.6 应用一元二次方程同步测试卷 2021—2022学年北师大版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2 m,另一边减少了3 m,剩余一块面积为20 m2的矩形空地.设原正方形空地的边长为x m,则下面所列方程正确的是( )
A.
B.
C.
D.
如图,在一块宽为20 m,长为32 m的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余(阴影)部分的面积为540 m2,则小路的宽应是( )
A. B. C. D.
一个面积为20的长方形场地一边利用现有的墙(墙长6米),另三边用13m的铁丝网围成,则这个长方形场地的周长是( )
A. 米 B. 米 C. 米或米 D. 不能确定
一块长和宽为30cm和20cm的长方形铁皮,在它的四角截去一个相等的小正方形折成一个无盖的长方体水槽,使它的侧面积为92平方厘米,则截去正方形边长为()厘米
A. B. C. 或 D. 或
如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',若两个三角形重叠部分的面积为,则它移动的距离AA'等于()
A. B. C. D.
如图,在中,,,,动点,分别从点,同时开始移动(移动方向如图所示),点的速度为,点的速度为,点移动到点后停止,点也随之停止运动,若使的面积为,则点运动的时间是( )
A. B. C. D.
如图所示,在Rt△ABC中,∠C=90°,AC=11cm,点P从点A出发沿AC以1cm/s的速度移动,点Q从点C出发沿CB以2cm/s的速度移动,如果P,Q分别从A,C两点同时出发,当它们相距10cm时所需的时间为( )
A. B.
C. D. 或
某中学组织初三学生篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有多少个班级参赛?()
A. B. C. D.
在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,则参加活动的同学有()
A. 人 B. 人 C. 人 D. 人
有一人患流感,经过两轮传染后,共有49人患了流感.如果不及时控制,第三轮被传染的人数为( )
A. 人 B. 人 C. 人 D. 人
“低碳生活,绿色出行”,电动汽车将逐渐代替燃油汽车,成为人们出行的主要交通工具,某城市一汽车销售4S店,今年2月份销售电动汽车共计64辆,4月份销售电动汽车共计100辆.若每月汽车销售增长率相同,则该汽车销售4S店5月份能销售电动汽车()
A. 辆 B. 辆 C. 辆 D. 辆
超市经销一种水果,每千克盈利10元,每天销售500千克,经市场调查,若每千克涨价1元,日销售量减少20千克,现超市要保证每天盈利6000元,每千克应涨价为( )
A. 元或元 B. 元或元 C. 元 D. 元或元
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售,尽快减少库存,商场决定采取降价措施,调查发现,每件衬衫,每降价1元,平均每天可多销售2件,若商场每天要盈利1200元,每件衬衫应降价()
A. 元 B. 元 C. 元 D. 元或元
二、填空题(本大题共4小题,共12分)
为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为______________.
如图,点阵M的层数用n表示,点数总和用S表示,当S=66时,则n=________.
某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店的销售额平均每月的增长率是________.
一个两位数.十位上的数字比个位上的数字大7,且十位上的数字与个位上的数字和的平方等于这个两位数,这个两位数是________.
三、解答题(本大题共6小题,共69分)
2020年年初,受新型冠状病毒的影响, 口罩成为最紧缺的物资之一.花都区某服装厂快速转型生产某种型号的矩形防护口罩.如图,已知该口罩长为18 cm,宽为9 cm.口罩上压边宽度是下压边宽度的2倍,左右压边与下压边同宽.
(1)设口罩下压边宽度为x cm,则口罩的上压边宽度为 cm;
(2)要使口罩内部有效面积(即图中空白部分)达到,则口罩下压边宽度为多少
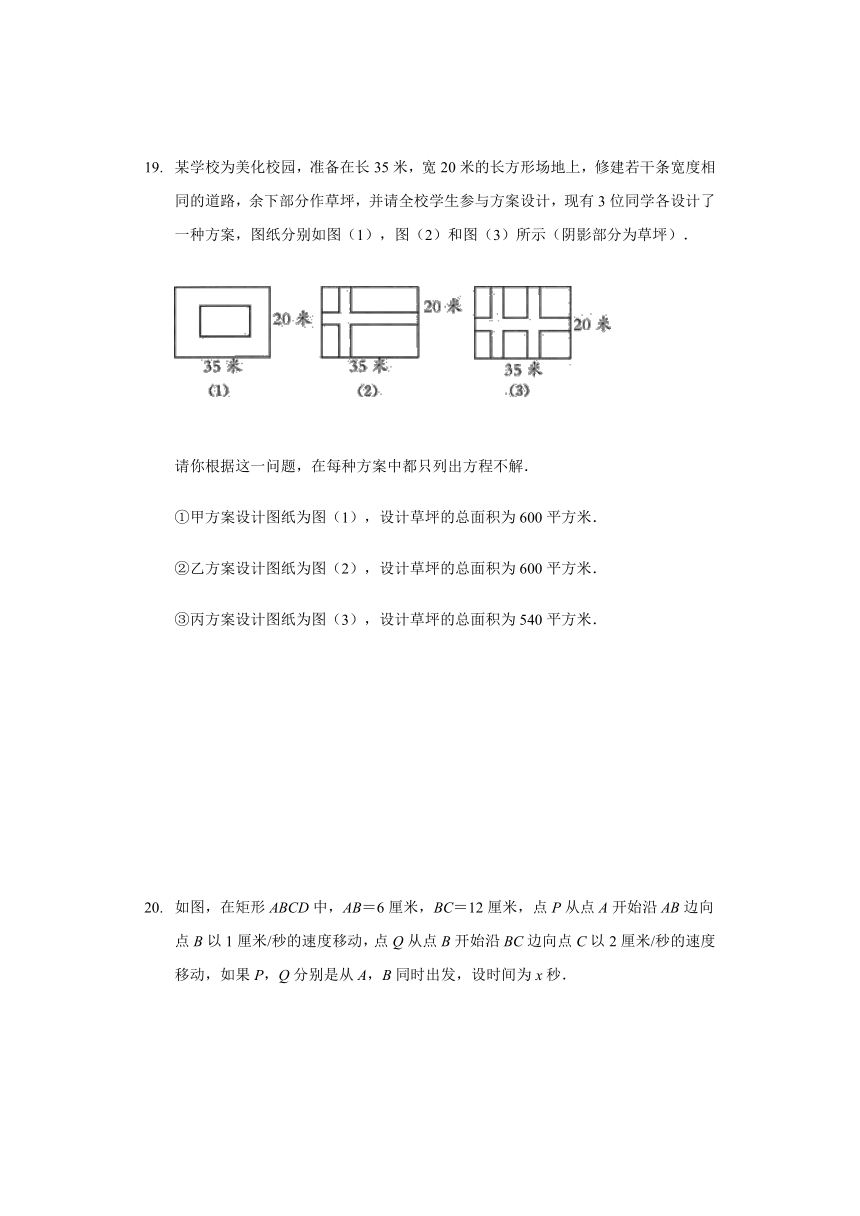
某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图(1),图(2)和图(3)所示(阴影部分为草坪).
请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图(1),设计草坪的总面积为600平方米.
②乙方案设计图纸为图(2),设计草坪的总面积为600平方米.
③丙方案设计图纸为图(3),设计草坪的总面积为540平方米.
如图,在矩形ABCD中,AB=6厘米,BC=12厘米,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P,Q分别是从A,B同时出发,设时间为x秒.
(1)经过几秒时,△PBQ的面积等于8平方厘米?
(2)经过几秒时,△PBQ的面积等于矩形面积的?
某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售时,平均每天可售出100千克,后来经过市场调查发现,单价每降低1元,则平均每天的销售可增加20千克.若该专卖店销售这种核桃要想平均每天获利2880元,求每千克核桃应降价多少元.
解:设每千克核桃应降价x元.
(1)用含x的代数式表示:
降价后,每千克核桃获利 元,平均每天可售出 千克核桃.
(2)根据题意,列出相应方程: .
(3)解这个方程,得 .
(4)答:每千克核桃应降价 元.
一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下, 经过一段时间销售, 发现销售单价每降低1元, 平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元
23.某旅游景点为了吸引游客,推出的团体票收费标准如下:如果团体人数不超过25人,每张票价150元;如果超过25人,每增加1人,每张票价降低2元,但每张票价不得低于100元.若阳光旅行社共支付团体票价4800元,则阳光旅行社共购买多少张团体票?
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】C
12.【答案】D
13.【答案】C
14.【答案】x(x+40)=1200
15.【答案】11
16.【答案】50%
17.【答案】81
18.【答案】解:(1)2x;
(2)依题意有(18-2x)(9-3x)=96,
解得=1,=11(不合题意,舍去).
故口罩下压边宽度为1 cm.
19.【答案】解:①设道路的宽为x米.依题意得:
(35-2x)(20-2x)=600;
②设道路的宽为x米.依题意得:(35-x)(20-x)=600;
③设道路的宽为x米.依题意得:(35-2x)(20-x)=540.
20.【答案】解:(1)PB=(6-x)厘米,BQ=2x厘米.
根据题意,得,
整理,得x2-6x+8=0,
解得x1=2,x2=4.
故经过2秒或4秒时,△PBQ的面积等于8平方厘米.
(2)PB=(6-x)厘米,BQ=2x厘米,
根据题意,得,
整理,得x2-6x+6=0,
解得,.
故经过秒或秒时,△PBQ的面积等于矩形面积的.
21.【答案】(1)(20-x);(100+20x) ;
(2)(20-x)(100+20x)=2880 ;
(3)=4,=11 ;
(4)4或11.
22.【答案】解:(1)26.
(2)设当每件商品降价x元时,该商店每天销售利润为1200元.
根据题意,得(40-x)(20+2x)=1200,整理,得-30x+200=0,
解得=10,=20.
要求每件盈利不少于25元,x=10.
答:当每件商品降价10元时,该商店每天销售利润为1200元.
23.【答案】解:∵150×25=3750<4800,
∴购买的团体票超过25张,
设共购买了x张团体票,
由题意列方程得x×[150-2(x-25)]=4800,
x2-100x+2400=0,
解得x1=60,x2=40,
当x1=60时,超过25人的人数为35人,票价降70元,降价后为150-70=80元<100元,不符题意,舍去,
x2=40符合题意,∴x=40,
答:共购买了40张团体票.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2 m,另一边减少了3 m,剩余一块面积为20 m2的矩形空地.设原正方形空地的边长为x m,则下面所列方程正确的是( )
A.
B.
C.
D.
如图,在一块宽为20 m,长为32 m的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余(阴影)部分的面积为540 m2,则小路的宽应是( )
A. B. C. D.
一个面积为20的长方形场地一边利用现有的墙(墙长6米),另三边用13m的铁丝网围成,则这个长方形场地的周长是( )
A. 米 B. 米 C. 米或米 D. 不能确定
一块长和宽为30cm和20cm的长方形铁皮,在它的四角截去一个相等的小正方形折成一个无盖的长方体水槽,使它的侧面积为92平方厘米,则截去正方形边长为()厘米
A. B. C. 或 D. 或
如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',若两个三角形重叠部分的面积为,则它移动的距离AA'等于()
A. B. C. D.
如图,在中,,,,动点,分别从点,同时开始移动(移动方向如图所示),点的速度为,点的速度为,点移动到点后停止,点也随之停止运动,若使的面积为,则点运动的时间是( )
A. B. C. D.
如图所示,在Rt△ABC中,∠C=90°,AC=11cm,点P从点A出发沿AC以1cm/s的速度移动,点Q从点C出发沿CB以2cm/s的速度移动,如果P,Q分别从A,C两点同时出发,当它们相距10cm时所需的时间为( )
A. B.
C. D. 或
某中学组织初三学生篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有多少个班级参赛?()
A. B. C. D.
在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,则参加活动的同学有()
A. 人 B. 人 C. 人 D. 人
有一人患流感,经过两轮传染后,共有49人患了流感.如果不及时控制,第三轮被传染的人数为( )
A. 人 B. 人 C. 人 D. 人
“低碳生活,绿色出行”,电动汽车将逐渐代替燃油汽车,成为人们出行的主要交通工具,某城市一汽车销售4S店,今年2月份销售电动汽车共计64辆,4月份销售电动汽车共计100辆.若每月汽车销售增长率相同,则该汽车销售4S店5月份能销售电动汽车()
A. 辆 B. 辆 C. 辆 D. 辆
超市经销一种水果,每千克盈利10元,每天销售500千克,经市场调查,若每千克涨价1元,日销售量减少20千克,现超市要保证每天盈利6000元,每千克应涨价为( )
A. 元或元 B. 元或元 C. 元 D. 元或元
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售,尽快减少库存,商场决定采取降价措施,调查发现,每件衬衫,每降价1元,平均每天可多销售2件,若商场每天要盈利1200元,每件衬衫应降价()
A. 元 B. 元 C. 元 D. 元或元
二、填空题(本大题共4小题,共12分)
为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为______________.
如图,点阵M的层数用n表示,点数总和用S表示,当S=66时,则n=________.
某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店的销售额平均每月的增长率是________.
一个两位数.十位上的数字比个位上的数字大7,且十位上的数字与个位上的数字和的平方等于这个两位数,这个两位数是________.
三、解答题(本大题共6小题,共69分)
2020年年初,受新型冠状病毒的影响, 口罩成为最紧缺的物资之一.花都区某服装厂快速转型生产某种型号的矩形防护口罩.如图,已知该口罩长为18 cm,宽为9 cm.口罩上压边宽度是下压边宽度的2倍,左右压边与下压边同宽.
(1)设口罩下压边宽度为x cm,则口罩的上压边宽度为 cm;
(2)要使口罩内部有效面积(即图中空白部分)达到,则口罩下压边宽度为多少
某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图(1),图(2)和图(3)所示(阴影部分为草坪).
请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图(1),设计草坪的总面积为600平方米.
②乙方案设计图纸为图(2),设计草坪的总面积为600平方米.
③丙方案设计图纸为图(3),设计草坪的总面积为540平方米.
如图,在矩形ABCD中,AB=6厘米,BC=12厘米,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P,Q分别是从A,B同时出发,设时间为x秒.
(1)经过几秒时,△PBQ的面积等于8平方厘米?
(2)经过几秒时,△PBQ的面积等于矩形面积的?
某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售时,平均每天可售出100千克,后来经过市场调查发现,单价每降低1元,则平均每天的销售可增加20千克.若该专卖店销售这种核桃要想平均每天获利2880元,求每千克核桃应降价多少元.
解:设每千克核桃应降价x元.
(1)用含x的代数式表示:
降价后,每千克核桃获利 元,平均每天可售出 千克核桃.
(2)根据题意,列出相应方程: .
(3)解这个方程,得 .
(4)答:每千克核桃应降价 元.
一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下, 经过一段时间销售, 发现销售单价每降低1元, 平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元
23.某旅游景点为了吸引游客,推出的团体票收费标准如下:如果团体人数不超过25人,每张票价150元;如果超过25人,每增加1人,每张票价降低2元,但每张票价不得低于100元.若阳光旅行社共支付团体票价4800元,则阳光旅行社共购买多少张团体票?
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】B
10.【答案】D
11.【答案】C
12.【答案】D
13.【答案】C
14.【答案】x(x+40)=1200
15.【答案】11
16.【答案】50%
17.【答案】81
18.【答案】解:(1)2x;
(2)依题意有(18-2x)(9-3x)=96,
解得=1,=11(不合题意,舍去).
故口罩下压边宽度为1 cm.
19.【答案】解:①设道路的宽为x米.依题意得:
(35-2x)(20-2x)=600;
②设道路的宽为x米.依题意得:(35-x)(20-x)=600;
③设道路的宽为x米.依题意得:(35-2x)(20-x)=540.
20.【答案】解:(1)PB=(6-x)厘米,BQ=2x厘米.
根据题意,得,
整理,得x2-6x+8=0,
解得x1=2,x2=4.
故经过2秒或4秒时,△PBQ的面积等于8平方厘米.
(2)PB=(6-x)厘米,BQ=2x厘米,
根据题意,得,
整理,得x2-6x+6=0,
解得,.
故经过秒或秒时,△PBQ的面积等于矩形面积的.
21.【答案】(1)(20-x);(100+20x) ;
(2)(20-x)(100+20x)=2880 ;
(3)=4,=11 ;
(4)4或11.
22.【答案】解:(1)26.
(2)设当每件商品降价x元时,该商店每天销售利润为1200元.
根据题意,得(40-x)(20+2x)=1200,整理,得-30x+200=0,
解得=10,=20.
要求每件盈利不少于25元,x=10.
答:当每件商品降价10元时,该商店每天销售利润为1200元.
23.【答案】解:∵150×25=3750<4800,
∴购买的团体票超过25张,
设共购买了x张团体票,
由题意列方程得x×[150-2(x-25)]=4800,
x2-100x+2400=0,
解得x1=60,x2=40,
当x1=60时,超过25人的人数为35人,票价降70元,降价后为150-70=80元<100元,不符题意,舍去,
x2=40符合题意,∴x=40,
答:共购买了40张团体票.
第1页,共1页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
