2021-2022学年湘教版数学九年级下册2.7 正多边形与圆 同步练习卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级下册2.7 正多边形与圆 同步练习卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 343.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 00:00:00 | ||
图片预览

文档简介
2021年湘教版数学九年级下册
2.7《正多边形与圆》同步练习卷
一、选择题
1.对于一个正多边形,下列四个命题中,错误的是 ( )
A.正多边形是轴对称图形,每条边的垂直平分线是它的对称轴
B.正多边形是中心对称图形,正多边形的中心是它的对称中心
C.正多边形每一个外角都等于正多边形的中心角
D.正多边形每一个内角都与正多边形的中心角互补
2.如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( )
A.60° B.45° C.30° D.22.5°
3.若正六边形的半径为4,则它的边长等于( )
A.4 B.2 C.2 D.4
4.圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )
A.扩大了一倍 B.扩大了两倍 C.扩大了四倍 D.没有变化
5.已知正六边形的边长为2,则它的内切圆的半径为( )
A.1 B. C.2 D.2
6.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
7.如图,P,Q分别是⊙O的内接正五边形的边AB,BC上的点,BP=CQ,则∠POQ=( )
A.75° B.54° C.72° D.60°
8.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( )
A.6π B.18 C.18π D.20
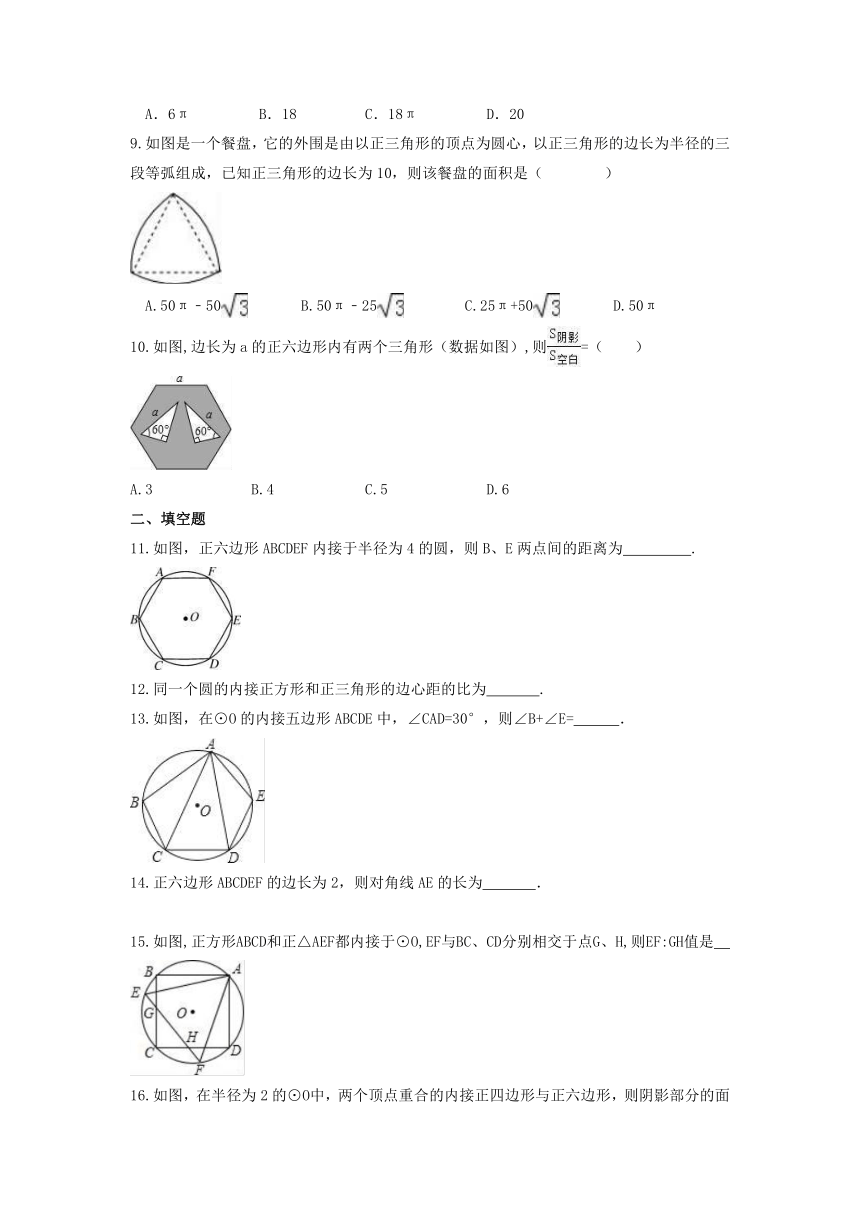
9.如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
A.50π﹣50 B.50π﹣25 C.25π+50 D.50π
10.如图,边长为a的正六边形内有两个三角形(数据如图),则=( )
A.3 B.4 C.5 D.6
二、填空题
11.如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为 .
12.同一个圆的内接正方形和正三角形的边心距的比为 .
13.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
14.正六边形ABCDEF的边长为2,则对角线AE的长为 .
15.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则EF:GH值是
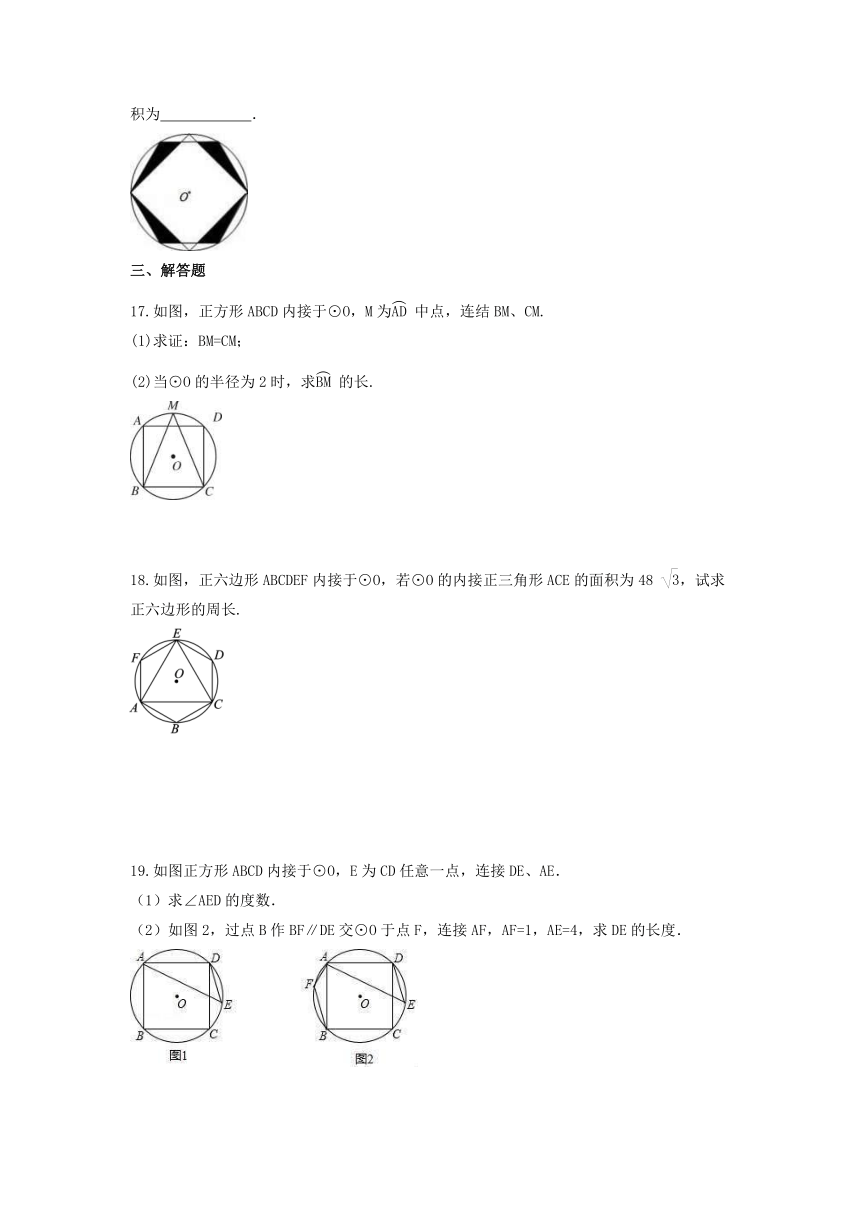
16.如图,在半径为2的⊙O中,两个顶点重合的内接正四边形与正六边形,则阴影部分的面积为 .
三、解答题
17.如图,正方形ABCD内接于⊙O,M为中点,连结BM、CM.
(1)求证:BM=CM;
(2)当⊙O的半径为2时,求的长.
18.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48 ,试求正六边形的周长.
19.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
20.如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
参考答案
1.B
2.C.
3.A.
4.D
5.B.
6.A.
7.C.
8.B
9.A
10.C
11.答案为:8.
12.答案为::1.
13.答案为:210°.
14.答案为:2.
15.答案为:.
16.答案为:6﹣2
17. (1)证明:∵四边形ABCD是正方形,
∴AB=CD,∴=.
∵M为中点,∴=,
∴+=+,即=,
∴BM=CM.
(2)解:∵⊙O的半径为2,∴⊙O的周长为4π.
∵===,∴=+=,
∴的长=× ×4π=×4π=π.
18.解:如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,
由勾股定理可得AH=== R.
而△ACE的面积是△OAH面积的6倍,
即6×× R×R=48 ,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
19.解:(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,解得x=或(舍弃),
∴DE=DH=
20.解:(1)如图,连接OB,OC.
∵正三角形ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,
∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
(2)90°,72°
(3)∠MON=.
2.7《正多边形与圆》同步练习卷
一、选择题
1.对于一个正多边形,下列四个命题中,错误的是 ( )
A.正多边形是轴对称图形,每条边的垂直平分线是它的对称轴
B.正多边形是中心对称图形,正多边形的中心是它的对称中心
C.正多边形每一个外角都等于正多边形的中心角
D.正多边形每一个内角都与正多边形的中心角互补
2.如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( )
A.60° B.45° C.30° D.22.5°
3.若正六边形的半径为4,则它的边长等于( )
A.4 B.2 C.2 D.4
4.圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )
A.扩大了一倍 B.扩大了两倍 C.扩大了四倍 D.没有变化
5.已知正六边形的边长为2,则它的内切圆的半径为( )
A.1 B. C.2 D.2
6.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
7.如图,P,Q分别是⊙O的内接正五边形的边AB,BC上的点,BP=CQ,则∠POQ=( )
A.75° B.54° C.72° D.60°
8.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( )
A.6π B.18 C.18π D.20
9.如图是一个餐盘,它的外围是由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,已知正三角形的边长为10,则该餐盘的面积是( )
A.50π﹣50 B.50π﹣25 C.25π+50 D.50π
10.如图,边长为a的正六边形内有两个三角形(数据如图),则=( )
A.3 B.4 C.5 D.6
二、填空题
11.如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为 .
12.同一个圆的内接正方形和正三角形的边心距的比为 .
13.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
14.正六边形ABCDEF的边长为2,则对角线AE的长为 .
15.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则EF:GH值是
16.如图,在半径为2的⊙O中,两个顶点重合的内接正四边形与正六边形,则阴影部分的面积为 .
三、解答题
17.如图,正方形ABCD内接于⊙O,M为中点,连结BM、CM.
(1)求证:BM=CM;
(2)当⊙O的半径为2时,求的长.
18.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48 ,试求正六边形的周长.
19.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
20.如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
参考答案
1.B
2.C.
3.A.
4.D
5.B.
6.A.
7.C.
8.B
9.A
10.C
11.答案为:8.
12.答案为::1.
13.答案为:210°.
14.答案为:2.
15.答案为:.
16.答案为:6﹣2
17. (1)证明:∵四边形ABCD是正方形,
∴AB=CD,∴=.
∵M为中点,∴=,
∴+=+,即=,
∴BM=CM.
(2)解:∵⊙O的半径为2,∴⊙O的周长为4π.
∵===,∴=+=,
∴的长=× ×4π=×4π=π.
18.解:如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,
由勾股定理可得AH=== R.
而△ACE的面积是△OAH面积的6倍,
即6×× R×R=48 ,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
19.解:(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,解得x=或(舍弃),
∴DE=DH=
20.解:(1)如图,连接OB,OC.
∵正三角形ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,
∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
(2)90°,72°
(3)∠MON=.
