2021—2022学年北师大版九年级数学上册第二章 一元二次方程单元测试卷(word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版九年级数学上册第二章 一元二次方程单元测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 15:57:14 | ||
图片预览



文档简介
第二章一元二次方程单元测试卷 2021—2022学年北师大版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列方程中,为关于x的一元二次方程的是( )
A. B.
C. D.
用配方法解方程-2x-5=0时,原方程应变形为( )
A. B. C. D.
一元二次方程x2-x-2=0的解是( )
A. , B. ,
C. , D. ,
如果一元二次方程+3x+m=0有实数根,那么实数m的取值范围为( )
A. B. C. D.
根据下面表格中的对应值判断:
x 3.23 3.24 3.25 3.26
+bx+c -0.06 -0.02 0.03 0.09
方程+bx+c=0(a0,a,b,c为常数)的一个解x的范围是( )
A. B.
C. D.
某种品牌运动服经过两次降价,每件零售价由560元降为315元.已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A. B.
C. D.
若关于x的方程+(-1)x+a=0的两根互为相反数,则a的值为( )
A. B. C. D.
已知3是关于x的方程-(m+1)x+2m=0的一个实数根,并且这个方程的两个实数根恰好是等腰ABC的两条边的边长,则ABC的周长为( )
A. B. C. D. 或
将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,依此规律,若第n个图形有114个小圆,则n的值是( )
A. B. C. D.
已知实数a、b满足(a2+b2)2-2(a2+b2)=8,则a2+b2的值为( )
A. B. C. 或 D. 或
二、填空题(本大题共6小题,共18分)
要使代数式-6的值等于21,则x的值是 .
已知,是一元二次方程+x-3=0的两个根,则+= .
已知m是关于x的方程-2x-3=0的一个根,则-4m= .
一件工艺品进价100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降低1元出售,则每天可多售出4件,要使顾客尽量得到优惠,且每天获得的利润为3596元,每件工艺品需降价 元.
阅读材料:如果a,b是一元二次方程+x-1=0的两个实数根,则有+a-1=0,+b-1=0.创新应用:如果m,n是两个不相等的实数,且满足-m=3,-n=3,那么代数式-mn+2m+2010= .
如图,在ABC中,C=,AB=10cm,AC= 8 cm,点P从点A开始出发向点C以2cm/s的速度移动,点Q从点B出发向点C以1cm/s的速度移动.若P,Q分别同时从A,B出发,设运动时间为ts,当四边形APQB的面积是时,t的值为 .
三、计算题(本大题共1小题,共6分)
解方程:
+3x-2=0.
(2)+3x+3=0.
(3)=x(3x+2)-7.
四、解答题(本大题共6小题,共66分)
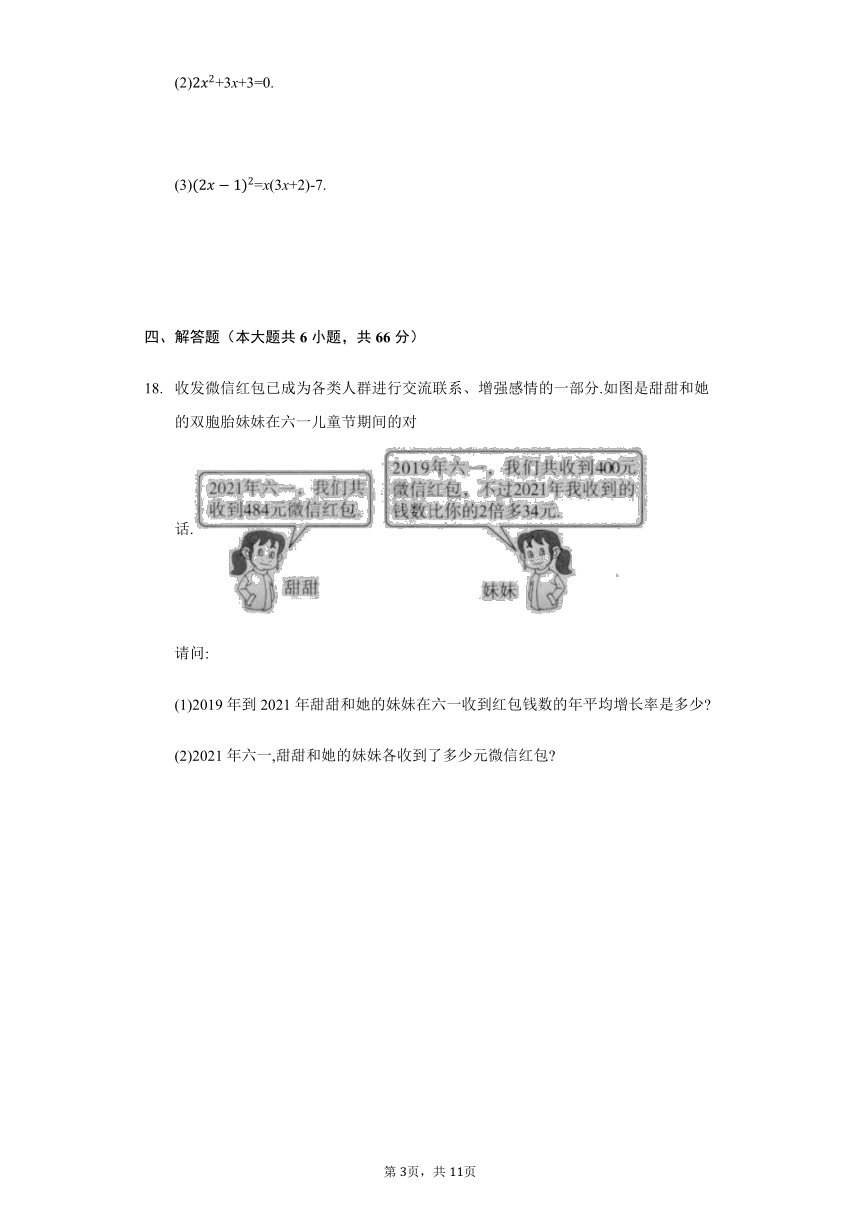
收发微信红包已成为各类人群进行交流联系、增强感情的一部分.如图是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:
(1)2019年到2021年甜甜和她的妹妹在六一收到红包钱数的年平均增长率是多少
(2)2021年六一,甜甜和她的妹妹各收到了多少元微信红包
阅读以下内容,解答下列问题.
我们知道,计算n边形的对角线条数公式为n(n-3).如果一个n边形共有20条对角线,那么可以得到方程n(n-3)=20.整理得-3n-40=0,解得n=8或n=-5.
n3,n=-5不合题意,舍去.
n=8,即该多边形是八边形.
(1)若一个多边形共有14条对角线,则这个多边形的边数是多少
(2)A同学说:“我求得一个多边形共有10条对角线.”你认为A同学的说法正确吗 为什么
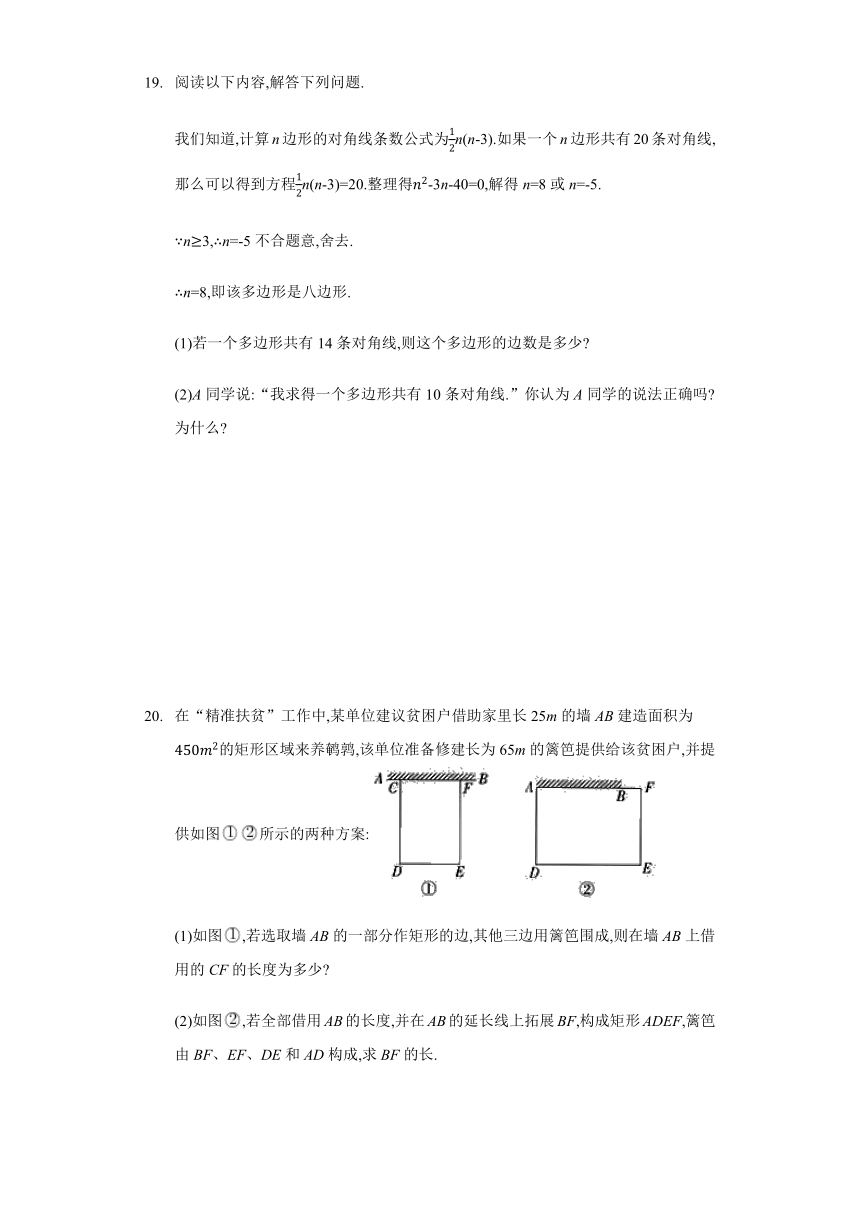
在“精准扶贫”工作中,某单位建议贫困户借助家里长25m的墙AB建造面积为的矩形区域来养鹌鹑,该单位准备修建长为65m的篱笆提供给该贫困户,并提供如图所示的两种方案:
(1)如图,若选取墙AB的一部分作矩形的边,其他三边用篱笆围成,则在墙AB上借用的CF的长度为多少
(2)如图,若全部借用AB的长度,并在AB的延长线上拓展BF,构成矩形ADEF,篱笆由BF、EF、DE和AD构成,求BF的长.
已知关于x的一元二次方程-(3k+1)x++2k=0.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=6,另两边长b,c恰好是这个方程的两个根,求此三角形的另两边长.
某地大力发展经济作物,其中果树种植已初具规模,今年受气候、雨水等因素的影响,樱桃较去年有小幅度的减产,而枇杷有所增产.(1)该地某果农今年收获樱桃和枇杷共400千克,其中枇杷的产量不超过樱桃产量的7倍,该果农今年收获樱桃至少多少千克
(2) 该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售,该果农去年樱桃的市场销售量为100千克,销售均价为30元/千克,今年樱桃的市场销售量比去年减少了m%,销售均价与去年相同;该果农去年枇杷的市场销售量为200千克,销售均价为20元/千克,今年枇杷的市场销售量比去年增加了2m%,但销售均价比去年减少了m%.若该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额与他去年樱桃和枇杷的市场销售总金额相同,求m的值.
如图,正方形ABCD的边长为4cm,动点P从点B出发,以2cm/s的速度沿B→C→D的方向向点D运动;动点Q从点A出发,以1cm/s的速度沿A→B的方向向点B运动.若P、Q两点同时出发,运动时间为t s.
(1)连接PD、PQ、DQ,当t为何值时,△PQD的面积为11cm2?
(2)当点P在BC上运动时,是否存在这样的t,使得△PQD是以PD为一腰的等腰三角形?若存在,请求出符合条件的t的值;若不存在,请说明理由.
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】3
12.【答案】-1
13.【答案】6
14.【答案】6
15.【答案】2021
16.【答案】2
17.【答案】解:(1)∵a=1,b=3,c=-2,
△=b2-4ac=9-4×1×(-2)=17,
∴,
=,=;
(2)∵a=2,b=3,c=3,
∴△=b2-4ac=9-4×2×3=-15<0,
∴原方程无实数根;
(3)原方程整理得:x2-6x+8=0,
(x-2)(x-4)=0,
x-2=0或x-4=0,
=2,=4.
18.【答案】解:(1)设收到红包钱数的年平均增长率是x,
根据题意,得400=484,
解得=-2.1(舍去),=0.1=10%.
答:2019年到2021年甜甜和她的妹妹在六一收到红包钱数的年平均增长率是10%.
(2)设甜甜收到了y元微信红包,则她的妹妹收到了(2y+34)元微信红包,
根据题意,得y+2y+34=484,
解得y=150,则2y+34=334.
答:2021年六一,甜甜和她的妹妹分别收到了150元和334元微信红包.
19.【答案】解:(1)设这个多边形的边数为n,
根据题意得n(n-3)=14,
整理得-3n-28=0,
解得n=7或n=-4.
n3,n=-4不合题意,舍去.
n=7,即这个多边形的边数是7.
(2)A同学的说法不正确.
理由如下:设这个多边形的边数为n,
则n(n-3)=10,
整理得-3n-20=0,
解得n=,
符合方程-3n-20=0的正整数n不存在,
多边形的对角线不可能有10条,即A同学的说法不正确.
20.【答案】解:(1)设CF的长为xm,则CD=m,
由题意得x=450,
解得=20,=45.
墙AB的长为25m,
x=45舍去,
CF=20m.
答:在墙AB上借助的CF的长度为20m.
(2)设BF的长为ym,则AD==(20-y)m,
由题意得(25+y)(20-y)=450,
解得=5,=-10(舍去),
BF=5m.
答:BF的长为5m.
21.【答案】(1)证明:由题意知=-4(+2k)=+6k+1--8k=-2k+1=0.
无论k取何实数值,方程总有实数根.
(2)解:ABC为等腰三角形,
有a=b=6,a=c=6或b=c三种情况.
当a=b=6或a=c=6时,可知x=6为方程的一个根,
-6(3k+1)++2k=0,
解得k=3或k=5.
当k=3时,方程为-10x+24=0,解得x=4或x=6,
三角形的另两边长为4,6.
当k=5时,方程为-16x+60=0,
解得x=6或x=10,
三角形的另两边长为6,10.
当b=c时,方程有两个相等的实数根,
=0,即=0,
解得==1,
方程为-4x+4=0,
解得==2,
此时三角形三边长为6,2,2,不满足三角形三边关系,故舍去.
综上可知,三角形的另两边长为4,6或6,10.
22.【答案】解:(1)该果农今年收获樱桃至少50千克.
(2)m的值为12.5.
23.【答案】解:(1)当点P在BC上时,即0≤t≤2.AQ=tcm,BQ=(4-t)cm,BP=2tcm,PC=(4-2t)cm,
∵S正方形ABCD=S△ADQ-S△BPQ-S△CPD=S△PQD,
∴.
解得t1=-1,t2=3,均不合题意,舍去.
当点P在CD上时,即2<t≤4,AQ=tcm,DP=(8-2t)cm,
∵,∴,
解得(不合题意,舍去).
∴不存在t的值,使△PQD的面积为11cm2.
(2)假设点P在BC上运动时,存在满足题意的t(0≤t≤2),
AQ=tcm,BQ=(4-t)cm,BP=2tcm,PC=(4-2t)cm,
当PD=QD时,∵∠C=∠A=90°,DC=DA,
∴Rt△DPC≌Rt△DQA,
∴PC=QA,即4-2t=t.解得;
当PD=PQ时,在Rt△PBQ中,=+=,
在Rt△PCD中,,
∴,
解得(不合题意,舍去),,
∴假设成立,
存在或,使得△PQD是以PD为一腰的等腰三角形.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列方程中,为关于x的一元二次方程的是( )
A. B.
C. D.
用配方法解方程-2x-5=0时,原方程应变形为( )
A. B. C. D.
一元二次方程x2-x-2=0的解是( )
A. , B. ,
C. , D. ,
如果一元二次方程+3x+m=0有实数根,那么实数m的取值范围为( )
A. B. C. D.
根据下面表格中的对应值判断:
x 3.23 3.24 3.25 3.26
+bx+c -0.06 -0.02 0.03 0.09
方程+bx+c=0(a0,a,b,c为常数)的一个解x的范围是( )
A. B.
C. D.
某种品牌运动服经过两次降价,每件零售价由560元降为315元.已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A. B.
C. D.
若关于x的方程+(-1)x+a=0的两根互为相反数,则a的值为( )
A. B. C. D.
已知3是关于x的方程-(m+1)x+2m=0的一个实数根,并且这个方程的两个实数根恰好是等腰ABC的两条边的边长,则ABC的周长为( )
A. B. C. D. 或
将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,依此规律,若第n个图形有114个小圆,则n的值是( )
A. B. C. D.
已知实数a、b满足(a2+b2)2-2(a2+b2)=8,则a2+b2的值为( )
A. B. C. 或 D. 或
二、填空题(本大题共6小题,共18分)
要使代数式-6的值等于21,则x的值是 .
已知,是一元二次方程+x-3=0的两个根,则+= .
已知m是关于x的方程-2x-3=0的一个根,则-4m= .
一件工艺品进价100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降低1元出售,则每天可多售出4件,要使顾客尽量得到优惠,且每天获得的利润为3596元,每件工艺品需降价 元.
阅读材料:如果a,b是一元二次方程+x-1=0的两个实数根,则有+a-1=0,+b-1=0.创新应用:如果m,n是两个不相等的实数,且满足-m=3,-n=3,那么代数式-mn+2m+2010= .
如图,在ABC中,C=,AB=10cm,AC= 8 cm,点P从点A开始出发向点C以2cm/s的速度移动,点Q从点B出发向点C以1cm/s的速度移动.若P,Q分别同时从A,B出发,设运动时间为ts,当四边形APQB的面积是时,t的值为 .
三、计算题(本大题共1小题,共6分)
解方程:
+3x-2=0.
(2)+3x+3=0.
(3)=x(3x+2)-7.
四、解答题(本大题共6小题,共66分)
收发微信红包已成为各类人群进行交流联系、增强感情的一部分.如图是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:
(1)2019年到2021年甜甜和她的妹妹在六一收到红包钱数的年平均增长率是多少
(2)2021年六一,甜甜和她的妹妹各收到了多少元微信红包
阅读以下内容,解答下列问题.
我们知道,计算n边形的对角线条数公式为n(n-3).如果一个n边形共有20条对角线,那么可以得到方程n(n-3)=20.整理得-3n-40=0,解得n=8或n=-5.
n3,n=-5不合题意,舍去.
n=8,即该多边形是八边形.
(1)若一个多边形共有14条对角线,则这个多边形的边数是多少
(2)A同学说:“我求得一个多边形共有10条对角线.”你认为A同学的说法正确吗 为什么
在“精准扶贫”工作中,某单位建议贫困户借助家里长25m的墙AB建造面积为的矩形区域来养鹌鹑,该单位准备修建长为65m的篱笆提供给该贫困户,并提供如图所示的两种方案:
(1)如图,若选取墙AB的一部分作矩形的边,其他三边用篱笆围成,则在墙AB上借用的CF的长度为多少
(2)如图,若全部借用AB的长度,并在AB的延长线上拓展BF,构成矩形ADEF,篱笆由BF、EF、DE和AD构成,求BF的长.
已知关于x的一元二次方程-(3k+1)x++2k=0.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=6,另两边长b,c恰好是这个方程的两个根,求此三角形的另两边长.
某地大力发展经济作物,其中果树种植已初具规模,今年受气候、雨水等因素的影响,樱桃较去年有小幅度的减产,而枇杷有所增产.(1)该地某果农今年收获樱桃和枇杷共400千克,其中枇杷的产量不超过樱桃产量的7倍,该果农今年收获樱桃至少多少千克
(2) 该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售,该果农去年樱桃的市场销售量为100千克,销售均价为30元/千克,今年樱桃的市场销售量比去年减少了m%,销售均价与去年相同;该果农去年枇杷的市场销售量为200千克,销售均价为20元/千克,今年枇杷的市场销售量比去年增加了2m%,但销售均价比去年减少了m%.若该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额与他去年樱桃和枇杷的市场销售总金额相同,求m的值.
如图,正方形ABCD的边长为4cm,动点P从点B出发,以2cm/s的速度沿B→C→D的方向向点D运动;动点Q从点A出发,以1cm/s的速度沿A→B的方向向点B运动.若P、Q两点同时出发,运动时间为t s.
(1)连接PD、PQ、DQ,当t为何值时,△PQD的面积为11cm2?
(2)当点P在BC上运动时,是否存在这样的t,使得△PQD是以PD为一腰的等腰三角形?若存在,请求出符合条件的t的值;若不存在,请说明理由.
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】3
12.【答案】-1
13.【答案】6
14.【答案】6
15.【答案】2021
16.【答案】2
17.【答案】解:(1)∵a=1,b=3,c=-2,
△=b2-4ac=9-4×1×(-2)=17,
∴,
=,=;
(2)∵a=2,b=3,c=3,
∴△=b2-4ac=9-4×2×3=-15<0,
∴原方程无实数根;
(3)原方程整理得:x2-6x+8=0,
(x-2)(x-4)=0,
x-2=0或x-4=0,
=2,=4.
18.【答案】解:(1)设收到红包钱数的年平均增长率是x,
根据题意,得400=484,
解得=-2.1(舍去),=0.1=10%.
答:2019年到2021年甜甜和她的妹妹在六一收到红包钱数的年平均增长率是10%.
(2)设甜甜收到了y元微信红包,则她的妹妹收到了(2y+34)元微信红包,
根据题意,得y+2y+34=484,
解得y=150,则2y+34=334.
答:2021年六一,甜甜和她的妹妹分别收到了150元和334元微信红包.
19.【答案】解:(1)设这个多边形的边数为n,
根据题意得n(n-3)=14,
整理得-3n-28=0,
解得n=7或n=-4.
n3,n=-4不合题意,舍去.
n=7,即这个多边形的边数是7.
(2)A同学的说法不正确.
理由如下:设这个多边形的边数为n,
则n(n-3)=10,
整理得-3n-20=0,
解得n=,
符合方程-3n-20=0的正整数n不存在,
多边形的对角线不可能有10条,即A同学的说法不正确.
20.【答案】解:(1)设CF的长为xm,则CD=m,
由题意得x=450,
解得=20,=45.
墙AB的长为25m,
x=45舍去,
CF=20m.
答:在墙AB上借助的CF的长度为20m.
(2)设BF的长为ym,则AD==(20-y)m,
由题意得(25+y)(20-y)=450,
解得=5,=-10(舍去),
BF=5m.
答:BF的长为5m.
21.【答案】(1)证明:由题意知=-4(+2k)=+6k+1--8k=-2k+1=0.
无论k取何实数值,方程总有实数根.
(2)解:ABC为等腰三角形,
有a=b=6,a=c=6或b=c三种情况.
当a=b=6或a=c=6时,可知x=6为方程的一个根,
-6(3k+1)++2k=0,
解得k=3或k=5.
当k=3时,方程为-10x+24=0,解得x=4或x=6,
三角形的另两边长为4,6.
当k=5时,方程为-16x+60=0,
解得x=6或x=10,
三角形的另两边长为6,10.
当b=c时,方程有两个相等的实数根,
=0,即=0,
解得==1,
方程为-4x+4=0,
解得==2,
此时三角形三边长为6,2,2,不满足三角形三边关系,故舍去.
综上可知,三角形的另两边长为4,6或6,10.
22.【答案】解:(1)该果农今年收获樱桃至少50千克.
(2)m的值为12.5.
23.【答案】解:(1)当点P在BC上时,即0≤t≤2.AQ=tcm,BQ=(4-t)cm,BP=2tcm,PC=(4-2t)cm,
∵S正方形ABCD=S△ADQ-S△BPQ-S△CPD=S△PQD,
∴.
解得t1=-1,t2=3,均不合题意,舍去.
当点P在CD上时,即2<t≤4,AQ=tcm,DP=(8-2t)cm,
∵,∴,
解得(不合题意,舍去).
∴不存在t的值,使△PQD的面积为11cm2.
(2)假设点P在BC上运动时,存在满足题意的t(0≤t≤2),
AQ=tcm,BQ=(4-t)cm,BP=2tcm,PC=(4-2t)cm,
当PD=QD时,∵∠C=∠A=90°,DC=DA,
∴Rt△DPC≌Rt△DQA,
∴PC=QA,即4-2t=t.解得;
当PD=PQ时,在Rt△PBQ中,=+=,
在Rt△PCD中,,
∴,
解得(不合题意,舍去),,
∴假设成立,
存在或,使得△PQD是以PD为一腰的等腰三角形.
第1页,共1页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
