人教版 数学六年级上册 扇形的认识和扇形的面积(课件)(共25张PPT)
文档属性
| 名称 | 人教版 数学六年级上册 扇形的认识和扇形的面积(课件)(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 00:00:00 | ||
图片预览


文档简介
(共25张PPT)
扇形的认识及
扇形的面积
O
0
A
B
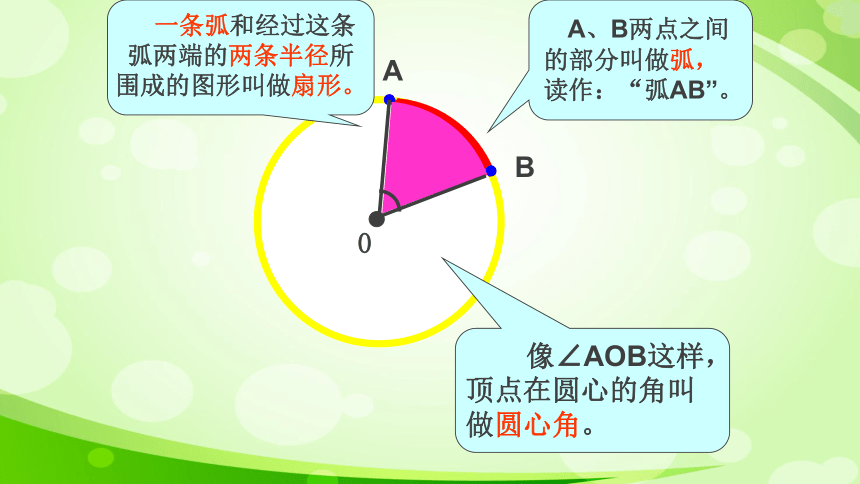
A、B两点之间的部分叫做弧,读作:“弧AB”。
像∠AOB这样,顶点在圆心的角叫做圆心角。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
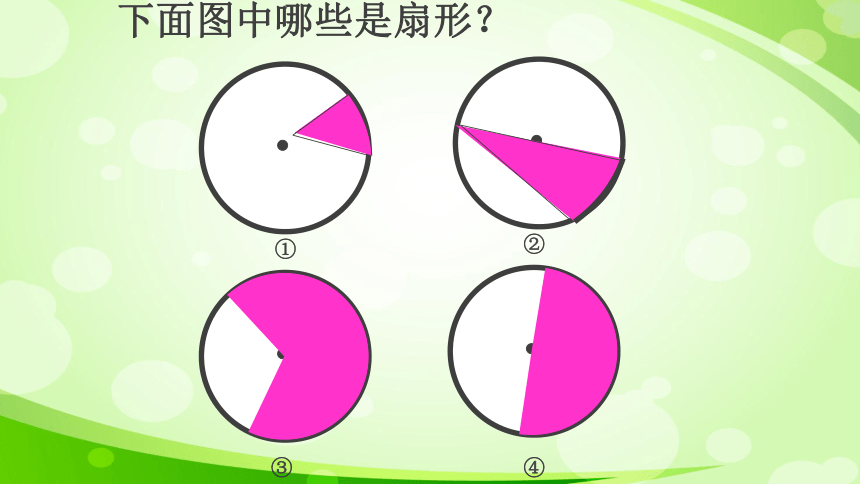
下面图中哪些是扇形?
①
②
③
④
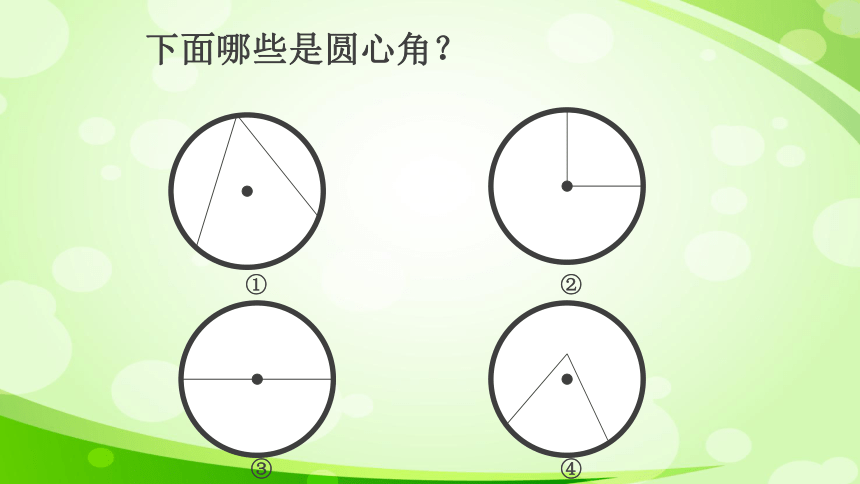
下面哪些是圆心角?
①
②
③
④
600
600
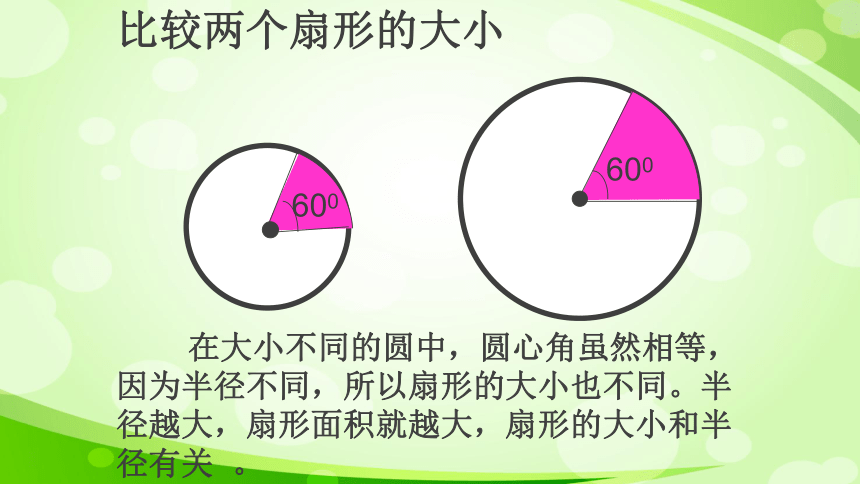
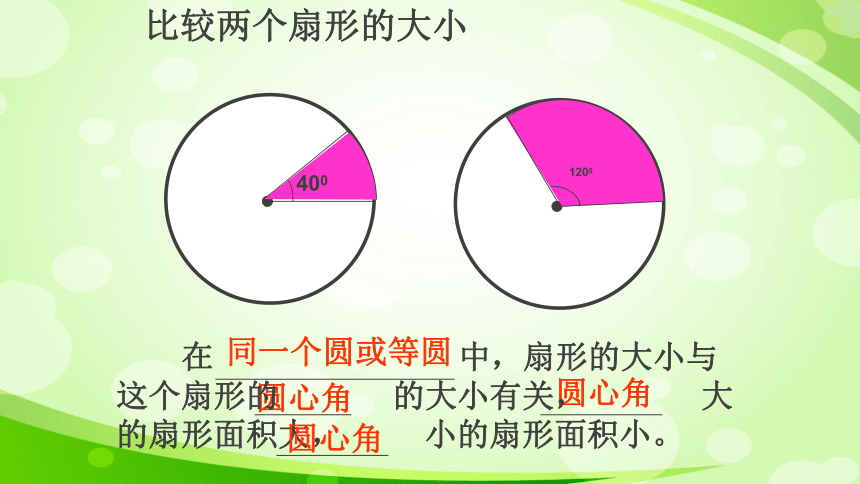
比较两个扇形的大小
在大小不同的圆中,圆心角虽然相等,因为半径不同,所以扇形的大小也不同。半径越大,扇形面积就越大,扇形的大小和半径有关 。
400
1200
比较两个扇形的大小
同一个圆或等圆
圆心角
圆心角
在 中,扇形的大小与这个扇形的 的大小有关, 大的扇形面积大, 小的扇形面积小。
圆心角
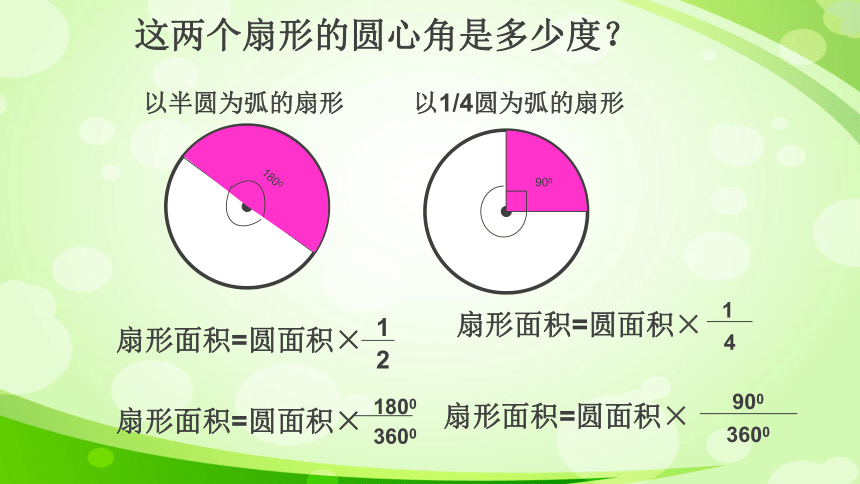
以半圆为弧的扇形
以1/4圆为弧的扇形
这两个扇形的圆心角是多少度?
900
扇形面积=圆面积×
2
1
扇形面积=圆面积×
4
1
1800
扇形面积=圆面积×
3600
1800
扇形面积=圆面积×
3600
900
例1:如图,n=60°,半径为6厘米,扇形的面积是多少?弧AB的长是多少?
答:扇形的面积是18.84平方厘米。弧AB的长是6.28厘米。
n
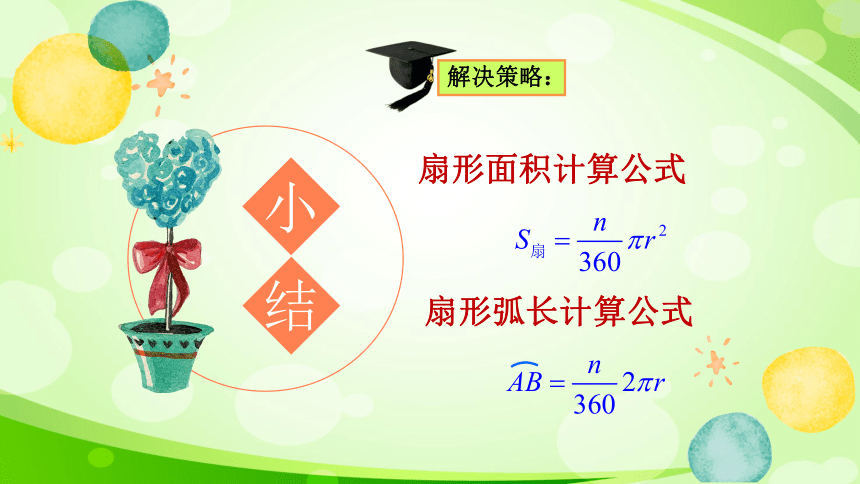
小
结
解决策略:
扇形面积计算公式
扇形弧长计算公式
例2:直角三角形AOC的直角边OA=6厘米,求弓形AC的面积。
答:弓形AC的面积是10.26平方厘米。
分析:弓形的面积不能直接求,可以考虑利用扇形面积减去三角形面积,其中:OA=OC=6,且圆心角∠AOC=90°。
小
结
解决策略:
例3:在一块长4.5米,宽2米的长方形铁板上截下2个最大的圆形后,剩下的铁板面积是多少平方米?
怎么截下两个最大的圆?
分析:剩下的铁板的面积可以用长方形铁板的面积减去两个圆形的面积,其中两个圆形铁板的直径均为2米。
答:剩下的铁板面积是2.72平方米。
2m
2m
4.5m
例4:从一块边长10厘米的正方形铁皮上剪下一个最大的圆,这块圆形铁皮的面积是多少平方厘米?剩下的面积是多少?
要圆形铁皮最大,其直径最大可以是正方形的边长。
答:这块圆形铁皮的面积是78.5平方厘米,剩下的面积是21.5平方厘米。
10cm
10cm
如图,你能求出正方形里面最大圆的面积吗?
—— 方中圆
正方形面积为 20 m
正方形面积为 8 m
正方形面积为n
该正方形面积与内最大圆之间有怎样的关系?
4︰π
如图
—— 圆中方
a
如果圆半径用a表示,圆里面最大正方形的面积是( ) ;
2a
圆的面积与最大正方形的面积之间有怎样的关系 ?
π︰2
求阴影部分的周长。(正方形边长都是4cm)
C1=____
C2=____
C3=____
12.56cm
28.56cm
20.56cm
C1> C3> C2
求阴影部分的面积。(正方形边长都是4cm)
S1=____
S2=____
S3=____
3.44cm2
3.44cm2
3.44cm2
S1= S2 = S3
求阴影部分的周长和面积。(正方形边长是4cm)
C=____
S=____
20.56cm
16cm2
不计算直接比较阴影部分的周长和面积。(单位:cm)
10
4
10
4
C1 __C2
s1 __s2
=
<
2、如下图,已知长方形的面积等于圆的面积,
求阴影部分的面积。
圆的半径为10厘米。
求周长
求面积
化零为整
平移(旋转)
等积代换
观察 → 转化 → 优化
例5:求下图中阴影部分的面积和周长。
分析:阴影部分的面积可以用大扇形的面积减去小扇形的面积。
例5:求下图中阴影部分的面积和周长。
周长是哪些部分?
例6:如图是一个钟面:分针长6cm。分针走了20分钟,分针旋转过的面积是多少平方厘米?
分析:旋转过的面积即以以分针长度为半径的扇形的面积,分针每分钟旋转( ), 20分钟转过了( )。
答:分针旋转过的面积是37.68平方厘米。
今天
你学到了什么
扇形面积弧长计算公式:
扇形的认识及
扇形的面积
O
0
A
B
A、B两点之间的部分叫做弧,读作:“弧AB”。
像∠AOB这样,顶点在圆心的角叫做圆心角。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
下面图中哪些是扇形?
①
②
③
④
下面哪些是圆心角?
①
②
③
④
600
600
比较两个扇形的大小
在大小不同的圆中,圆心角虽然相等,因为半径不同,所以扇形的大小也不同。半径越大,扇形面积就越大,扇形的大小和半径有关 。
400
1200
比较两个扇形的大小
同一个圆或等圆
圆心角
圆心角
在 中,扇形的大小与这个扇形的 的大小有关, 大的扇形面积大, 小的扇形面积小。
圆心角
以半圆为弧的扇形
以1/4圆为弧的扇形
这两个扇形的圆心角是多少度?
900
扇形面积=圆面积×
2
1
扇形面积=圆面积×
4
1
1800
扇形面积=圆面积×
3600
1800
扇形面积=圆面积×
3600
900
例1:如图,n=60°,半径为6厘米,扇形的面积是多少?弧AB的长是多少?
答:扇形的面积是18.84平方厘米。弧AB的长是6.28厘米。
n
小
结
解决策略:
扇形面积计算公式
扇形弧长计算公式
例2:直角三角形AOC的直角边OA=6厘米,求弓形AC的面积。
答:弓形AC的面积是10.26平方厘米。
分析:弓形的面积不能直接求,可以考虑利用扇形面积减去三角形面积,其中:OA=OC=6,且圆心角∠AOC=90°。
小
结
解决策略:
例3:在一块长4.5米,宽2米的长方形铁板上截下2个最大的圆形后,剩下的铁板面积是多少平方米?
怎么截下两个最大的圆?
分析:剩下的铁板的面积可以用长方形铁板的面积减去两个圆形的面积,其中两个圆形铁板的直径均为2米。
答:剩下的铁板面积是2.72平方米。
2m
2m
4.5m
例4:从一块边长10厘米的正方形铁皮上剪下一个最大的圆,这块圆形铁皮的面积是多少平方厘米?剩下的面积是多少?
要圆形铁皮最大,其直径最大可以是正方形的边长。
答:这块圆形铁皮的面积是78.5平方厘米,剩下的面积是21.5平方厘米。
10cm
10cm
如图,你能求出正方形里面最大圆的面积吗?
—— 方中圆
正方形面积为 20 m
正方形面积为 8 m
正方形面积为n
该正方形面积与内最大圆之间有怎样的关系?
4︰π
如图
—— 圆中方
a
如果圆半径用a表示,圆里面最大正方形的面积是( ) ;
2a
圆的面积与最大正方形的面积之间有怎样的关系 ?
π︰2
求阴影部分的周长。(正方形边长都是4cm)
C1=____
C2=____
C3=____
12.56cm
28.56cm
20.56cm
C1> C3> C2
求阴影部分的面积。(正方形边长都是4cm)
S1=____
S2=____
S3=____
3.44cm2
3.44cm2
3.44cm2
S1= S2 = S3
求阴影部分的周长和面积。(正方形边长是4cm)
C=____
S=____
20.56cm
16cm2
不计算直接比较阴影部分的周长和面积。(单位:cm)
10
4
10
4
C1 __C2
s1 __s2
=
<
2、如下图,已知长方形的面积等于圆的面积,
求阴影部分的面积。
圆的半径为10厘米。
求周长
求面积
化零为整
平移(旋转)
等积代换
观察 → 转化 → 优化
例5:求下图中阴影部分的面积和周长。
分析:阴影部分的面积可以用大扇形的面积减去小扇形的面积。
例5:求下图中阴影部分的面积和周长。
周长是哪些部分?
例6:如图是一个钟面:分针长6cm。分针走了20分钟,分针旋转过的面积是多少平方厘米?
分析:旋转过的面积即以以分针长度为半径的扇形的面积,分针每分钟旋转( ), 20分钟转过了( )。
答:分针旋转过的面积是37.68平方厘米。
今天
你学到了什么
扇形面积弧长计算公式:
