圆的面积(课件)数学六年级上册人教版(24张ppt)
文档属性
| 名称 | 圆的面积(课件)数学六年级上册人教版(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 14:53:58 | ||
图片预览






文档简介
(共24张PPT)
圆的面积
例1:求下面各圆的面积。
(1)半径 分米
(2)直径 米
(米)
(平方分米)
(平方米)
例1:求下面各圆的面积。
(3)周长 厘米
(厘米)
(平方厘米)
如何求r?
(4)直径 分米
(分米)
(平方分米)
分析:周长与半径的关系为:
2.计算下面各图的面积。
(1) (2)
即学即练
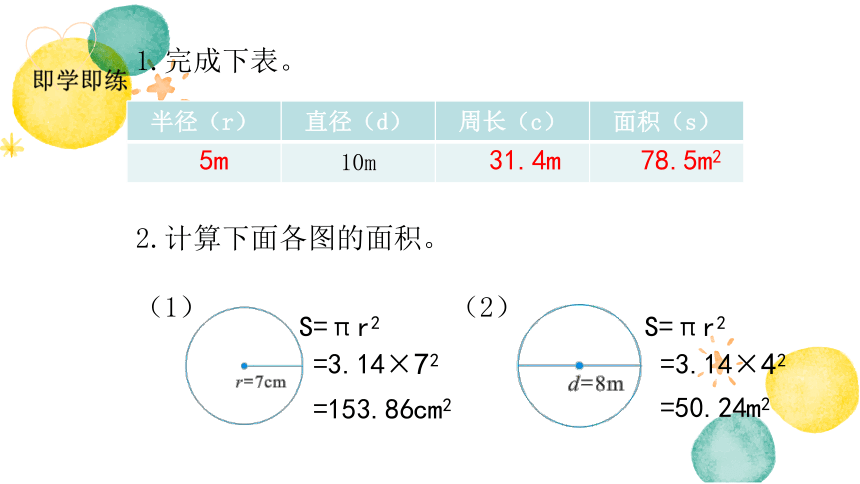
1.完成下表。
半径(r) 直径(d) 周长(c) 面积(s)
10m
S=πr2
5m
31.4m
78.5m2
=3.14×72
=153.86cm2
S=πr2
=3.14×42
=50.24m2
小
结
d=2r
解决策略:
圆的面积公式:
圆的直径半径的关系:
例2:一个圆形污水处理池的周长是31.4米。这个
污水处理池占地多少平方米?
(米)
(平方米)
分析:已知一个圆形的周长是31.4米,可以先根据
求出r,再求圆形水池的面积。
答:这个污水处理池占地 平方米。
即学即练
1.给一个俯视周长为62.8米的圆形水池底部贴瓷砖,求最少需要多少平方米的瓷砖?
2.用一根长12.56厘米的绳子围成一个最大的圆,求这个圆的面积。
r=62.8÷3.14÷2=10(m)
S=πr2=3.14×102=314(m2)
答:最少需要314平方米的瓷砖。
r=12.56÷3.14÷2=2(cm)
S=πr2=3.14×22=12.56(cm2)
答:这个圆的面积是12.56cm2。
小
结
任意一个圆的周长与它的直径的商是一个固定的数,我们把它叫做圆周率,用字母π 表示。它是一个无限不循环小数,计算时通常取3.14。用字母表示为:
C=πd
或C=2πr
解决策略:
例3:光盘银色部分是一个圆环,内圆半径是 ,
外圆半径是 。它的面积是多少?
圆环的面积等于大圆的面积减去小圆的面积。
答:它的面积是 平方厘米 。
即学即练
如图,给一个学校的跑道铺橡胶,需要铺多少平方米?
S=S圆环+2S长方形
答:需要铺3648.5平方米。
=3.14×(552-502)+200×5×2
=1648.5+2000
=3648.5(m2)
例4:下图中圆和长方形的面积相等,长方形的长
是 分米,你能求出圆的面积吗?
分析:要求圆的面积必须先求出圆
的半径,从图上观察圆的半径与长
方形有何关系?
圆的面积:
长方形的面积:
已知圆与长方形面积相等,则
得到:
长方形的宽=圆的半径,即 。
例4:如图,圆和长方形的面积相等,长方形的长
是 分米,你能求出圆的面积吗?
(平方分米)
答:圆的面积为 平方分米。
求得 分米,则
即学即练
1.如图,已知长方形的周长为6米,求一个圆的面积。
2.一根铁丝恰好可以围成一个边长是9.42dm的正方形,如果用这根铁丝围成一个圆,这个圆的面积是多少平方分米?(铁丝均无剩余)
d=6÷2÷3=1(m)
S=πr2=3.14×0.52=0.785(m2)
答:一个圆的面积是0.785m2。
r=9.42×4÷3.14÷2=6(dm)
S=πr2=3.14×62=113.04(dm2)
答:这个圆的面积是113.04dm2。
拓展提高
想一想
你会求下列图形的面积吗?
3cm
知道哪些条件就可求圆的面积?
(知道半径、直径或是周长)
总结
人民教育出版社 六年级 | 上册
1m
1m
1m
S正=a×a
=2×2
=4(m )
S正-S圆=4-3.14=0.86(m )
S圆= πr 2
=3.14×1
=3.14(m )
正方形的面积-圆的面积
圆的面积-正方形的面积
S正=S三×2
=(2×1÷2)×2
=2(m )
S圆= πr 2
=3.14×1
=3.14(m )
S圆-S正=3.14-2=1.14(m )
1m
底=直径=2m
高=半径=
1m
底=半径=1m
高=半径=
S正=S三×4
=(1×1÷2)×4
=2(m )
r
假设圆的半径为r,则三个图形的面积分别可以表示为。
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
r
外方内圆之间部分的面积:
外圆内方之间部分的面积:
4r -πr =0.86r
πr -2r =1.14r
r
假设圆的半径为r,则三个图形的面积分别可以表示为。
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
r
三个图形的面积比是:
外方内圆的面积比:
外圆内方的面积比:
4r :πr = 4:π
πr : 2r = π :2
4r :πr :2r
= 4:π:2
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。外面的圆与内部的正方形之间的面积是多少?
答:外面的圆与内部的正方形之间的面积约是164.16 cm 。
S正=S三×2
=24×(24÷2)÷2×2
=288(m )
S圆= πr 2
=3.14× (24÷2)
=452.16(m )
S圆-S正=452.16-288=164.16(m )
1.14r
=1.14×(24÷2)
=1.14×12
=164.16(m )
例5:下图是一枚清代铜钱的示意图,这枚清代铜钱的面积是多少平方厘米?
铜钱的面积
=圆形面积-正方形
3cm
0.8cm
答:这枚清代铜钱的面积是6.425平方厘米。
S圆=πr2=3.14×1.52=7.065(cm2)
S正=a2=0.8×0.8=0.64(cm2)
S铜钱=7.065-0.64=6.425(cm2)
即学即练
1.如图,用一张正方形的彩纸,剪出一个外圆最大的圆环,剩余纸张的面积是多少?(单位:厘米)
2.求下面图形中阴影部分的面积。(单位:分米)
S=S正方形-S圆环
=10×10-3.14×(52-22)
=100-65.94
=34.06(cm2)
S=S大圆-2S小圆
=3.14×62-2×3.14×32
=113.04-56.52
=56.52(dm2)
今天
你学到了什么
圆的面积公式:
圆的面积
例1:求下面各圆的面积。
(1)半径 分米
(2)直径 米
(米)
(平方分米)
(平方米)
例1:求下面各圆的面积。
(3)周长 厘米
(厘米)
(平方厘米)
如何求r?
(4)直径 分米
(分米)
(平方分米)
分析:周长与半径的关系为:
2.计算下面各图的面积。
(1) (2)
即学即练
1.完成下表。
半径(r) 直径(d) 周长(c) 面积(s)
10m
S=πr2
5m
31.4m
78.5m2
=3.14×72
=153.86cm2
S=πr2
=3.14×42
=50.24m2
小
结
d=2r
解决策略:
圆的面积公式:
圆的直径半径的关系:
例2:一个圆形污水处理池的周长是31.4米。这个
污水处理池占地多少平方米?
(米)
(平方米)
分析:已知一个圆形的周长是31.4米,可以先根据
求出r,再求圆形水池的面积。
答:这个污水处理池占地 平方米。
即学即练
1.给一个俯视周长为62.8米的圆形水池底部贴瓷砖,求最少需要多少平方米的瓷砖?
2.用一根长12.56厘米的绳子围成一个最大的圆,求这个圆的面积。
r=62.8÷3.14÷2=10(m)
S=πr2=3.14×102=314(m2)
答:最少需要314平方米的瓷砖。
r=12.56÷3.14÷2=2(cm)
S=πr2=3.14×22=12.56(cm2)
答:这个圆的面积是12.56cm2。
小
结
任意一个圆的周长与它的直径的商是一个固定的数,我们把它叫做圆周率,用字母π 表示。它是一个无限不循环小数,计算时通常取3.14。用字母表示为:
C=πd
或C=2πr
解决策略:
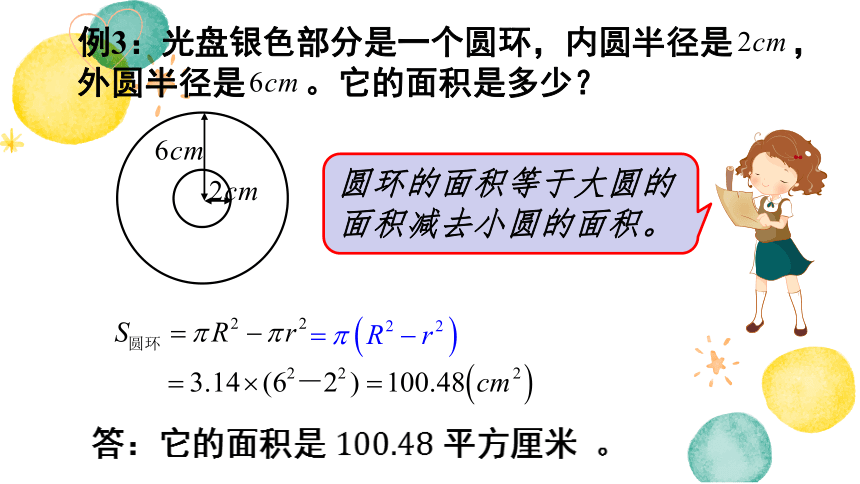
例3:光盘银色部分是一个圆环,内圆半径是 ,
外圆半径是 。它的面积是多少?
圆环的面积等于大圆的面积减去小圆的面积。
答:它的面积是 平方厘米 。
即学即练
如图,给一个学校的跑道铺橡胶,需要铺多少平方米?
S=S圆环+2S长方形
答:需要铺3648.5平方米。
=3.14×(552-502)+200×5×2
=1648.5+2000
=3648.5(m2)
例4:下图中圆和长方形的面积相等,长方形的长
是 分米,你能求出圆的面积吗?
分析:要求圆的面积必须先求出圆
的半径,从图上观察圆的半径与长
方形有何关系?
圆的面积:
长方形的面积:
已知圆与长方形面积相等,则
得到:
长方形的宽=圆的半径,即 。
例4:如图,圆和长方形的面积相等,长方形的长
是 分米,你能求出圆的面积吗?
(平方分米)
答:圆的面积为 平方分米。
求得 分米,则
即学即练
1.如图,已知长方形的周长为6米,求一个圆的面积。
2.一根铁丝恰好可以围成一个边长是9.42dm的正方形,如果用这根铁丝围成一个圆,这个圆的面积是多少平方分米?(铁丝均无剩余)
d=6÷2÷3=1(m)
S=πr2=3.14×0.52=0.785(m2)
答:一个圆的面积是0.785m2。
r=9.42×4÷3.14÷2=6(dm)
S=πr2=3.14×62=113.04(dm2)
答:这个圆的面积是113.04dm2。
拓展提高
想一想
你会求下列图形的面积吗?
3cm
知道哪些条件就可求圆的面积?
(知道半径、直径或是周长)
总结
人民教育出版社 六年级 | 上册
1m
1m
1m
S正=a×a
=2×2
=4(m )
S正-S圆=4-3.14=0.86(m )
S圆= πr 2
=3.14×1
=3.14(m )
正方形的面积-圆的面积
圆的面积-正方形的面积
S正=S三×2
=(2×1÷2)×2
=2(m )
S圆= πr 2
=3.14×1
=3.14(m )
S圆-S正=3.14-2=1.14(m )
1m
底=直径=2m
高=半径=
1m
底=半径=1m
高=半径=
S正=S三×4
=(1×1÷2)×4
=2(m )
r
假设圆的半径为r,则三个图形的面积分别可以表示为。
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
r
外方内圆之间部分的面积:
外圆内方之间部分的面积:
4r -πr =0.86r
πr -2r =1.14r
r
假设圆的半径为r,则三个图形的面积分别可以表示为。
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
r
三个图形的面积比是:
外方内圆的面积比:
外圆内方的面积比:
4r :πr = 4:π
πr : 2r = π :2
4r :πr :2r
= 4:π:2
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。外面的圆与内部的正方形之间的面积是多少?
答:外面的圆与内部的正方形之间的面积约是164.16 cm 。
S正=S三×2
=24×(24÷2)÷2×2
=288(m )
S圆= πr 2
=3.14× (24÷2)
=452.16(m )
S圆-S正=452.16-288=164.16(m )
1.14r
=1.14×(24÷2)
=1.14×12
=164.16(m )
例5:下图是一枚清代铜钱的示意图,这枚清代铜钱的面积是多少平方厘米?
铜钱的面积
=圆形面积-正方形
3cm
0.8cm
答:这枚清代铜钱的面积是6.425平方厘米。
S圆=πr2=3.14×1.52=7.065(cm2)
S正=a2=0.8×0.8=0.64(cm2)
S铜钱=7.065-0.64=6.425(cm2)
即学即练
1.如图,用一张正方形的彩纸,剪出一个外圆最大的圆环,剩余纸张的面积是多少?(单位:厘米)
2.求下面图形中阴影部分的面积。(单位:分米)
S=S正方形-S圆环
=10×10-3.14×(52-22)
=100-65.94
=34.06(cm2)
S=S大圆-2S小圆
=3.14×62-2×3.14×32
=113.04-56.52
=56.52(dm2)
今天
你学到了什么
圆的面积公式:
