6.3频数直方图 同步练习(含答案)
文档属性
| 名称 | 6.3频数直方图 同步练习(含答案) | 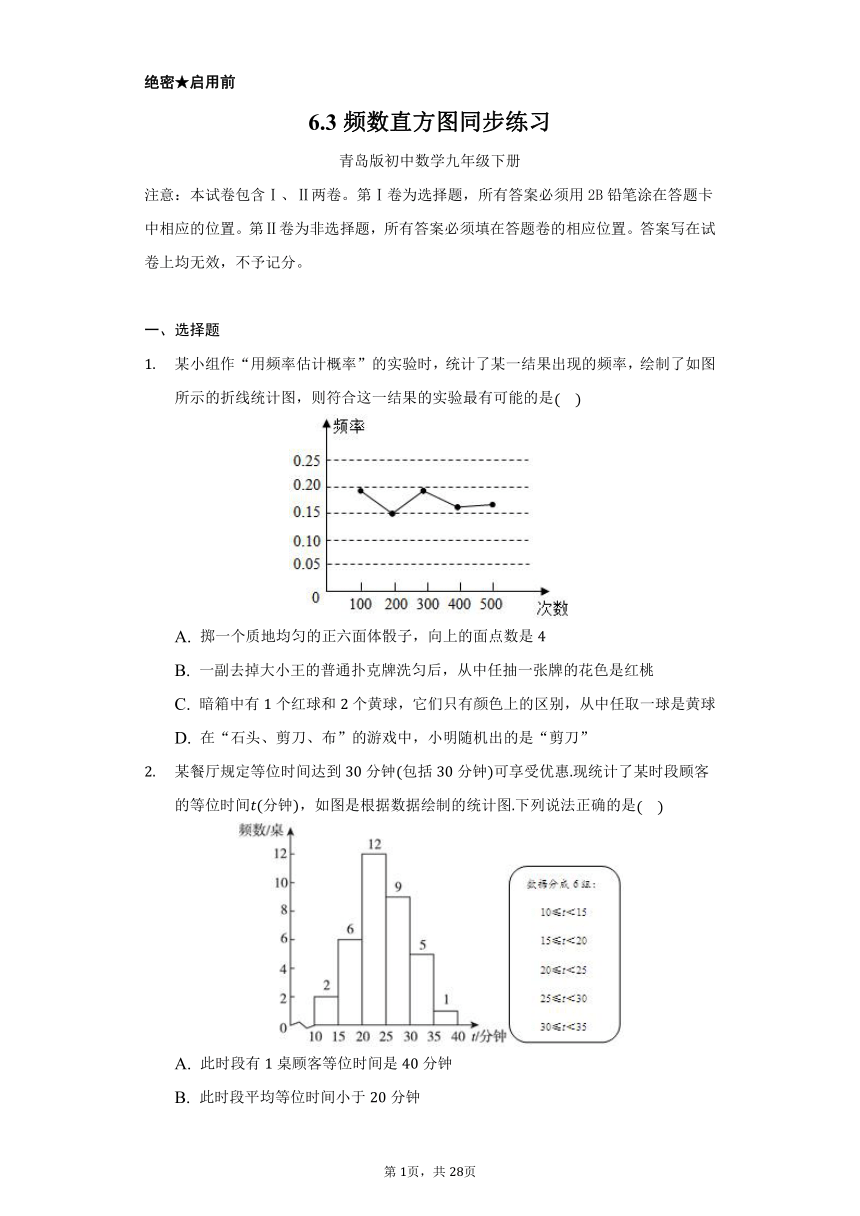 | |
| 格式 | docx | ||
| 文件大小 | 254.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 20:57:28 | ||
图片预览



文档简介
绝密★启用前
6.3频数直方图同步练习
青岛版初中数学九年级下册
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
一、选择题
某小组作“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是
A. 掷一个质地均匀的正六面体骰子,向上的面点数是
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有个红球和个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
某餐厅规定等位时间达到分钟包括分钟可享受优惠现统计了某时段顾客的等位时间分钟,如图是根据数据绘制的统计图下列说法正确的是
A. 此时段有桌顾客等位时间是分钟
B. 此时段平均等位时间小于分钟
C. 此时段等位时间的中位数可能是
D. 此时段有桌顾客可享受优惠
对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频数表如下:
抽取件数件
合格频数
若出售件衬衣,则其中的次品最接近件.
A. B. C. D.
生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解年某市第二季度日均可回收物回收量情况,随机抽取该市年第二季度的天数据,整理后绘制成统计表进行分析.
日均可回收物回收量千吨 合计
频数
频率
表中组的频率满足.
下面有四个推断:
表中的值为;
表中的值可以为;
这天的日均可回收物回收量的中位数在组;
这天的日均可回收物回收量的平均数不低于.
所有合理推断的序号是
A. B. C. D.
一个容量为的样本最大值为,最小值为,取组距为,则可以分成
A. 组 B. 组 C. 组 D. 组
某学校为了了解该学校七年级学生双休日上网的情况,随机调查了该学校七年级的名学生,得到了上周双休日上网时间的一组样本数据,其频数分布直方图如图所示,那么估计该学校七年级每名学生双休日上网的平均时间是
A. 小时 B. 小时 C. 小时 D. 小时
甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的折线统计图如图所示,符合这一结果的试验可能是
A. 掷一枚质地均匀的骰子,出现点朝上的频率
B. 任意写一个正整数,它能被整除的频率
C. 抛一枚硬币,出现正面朝上的频率
D. 从一个装有个白球和个红球的袋子中任取一球,取到白球的频率
某班有位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数分布直方图横半轴表示分数,把分到分之间的分数分成组,组距是分,纵半轴表示频数如图所示,从左到右的小矩形的高度比是::::,则由图可知,其中分数在之间的人数是
A. B. C. D.
某校组织部分学生参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是,,,,第五组的频数是则:
参加本次竞赛的学生共有人;
第五组的百分比为;
成绩在分的人数最多;
分以上的学生有名;
其中正确的个数有
A. 个 B. 个 C. 个 D. 个
如图,是九班名同学每周课外阅读时间的频数分布直方图每组含前一个边界值,不含后一个边界值,由图可知,每周课外阅读时间不小于小时的人数是
A. 人 B. 人 C. 人 D. 人
统计得到的一组数据有个,其中最大值为,最小值为,取组距为,可以分成
A. 组 B. 组 C. 组 D. 组
小文同学统计了某小区部分居民每周使用共享单车的时间,并绘制了统计图,如图所示.下面有四个推断:
小文此次一共调查了位小区居民;
每周使用时间不足的人数多于的人数;
每周使用时间超过的人数超过调查总人数的一半;
每周使用时间在的人数最多.
根据图中信息,上述说法中正确的是
A. B. C. D.
二、填空题
一个样本最大值为,最小值为,取组距为,则可以分成______组.
为了打赢“脱贫攻坚”战役,国家设立了“中央财政脱贫专项资金”以保证对各省贫困地区的持续投入.小莹同学通过登陆国家乡村振兴局网站,查询到了年中央财政脱贫专项资金对个省份的分配额度亿元,并对数据进行整理和分析.图是反映年中央财政脱贫专项资金分配额度的频数分布直方图,且在这一组分配的额度分别是:,,,,,,,,图是反映年中央财政脱贫专项资金对自治区和自治区的分配额度变化折线图.则下列说法中正确的是______.
A.年,中央财政脱贫专项资金对各省份的分配额度的中位数为亿元
B.年,某省获得的分配额度为亿元,该额度在个省份中由高到低排第六名
C.年,中央财政脱贫专项资金对自治区的分配额度逐年增加
D.年,中央财政脱贫专项资金对自治区的分配额度比对自治区的稳定
小夏同学从家到学校有,两条不同的公交线路为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了个班次的公交车,收集了这些班次的公交车用时单位:分钟的数据,统计如下:
公交车用时频数
公交车线 合计
据此估计,早高峰期间,乘坐线路“用时不超过分钟”的概率为______ ;若要在分钟之内到达学校,应尽量选择乘坐______ 填或线路.
对某班最近一次数学测试成绩得分取整数进行统计分析,全班共人,将分以上不含分的成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为及格分以上,不含分的在全班学生成绩中所占百分比为______ .
有个数据,其中最大值为,最小值为,若取组距为,则应该分成______组.
三、解答题
为迎接年冬奥会,鼓励更多的学生参与到志愿服务中学,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有名学生进入综合素质展开环节,为了了解两所学校这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了名学生的综合素质展示成绩百分制,并对数据成绩进行整理、描述和分析,下面给出了部分信息.
甲学校学生成绩的频数分布直方图如下数据分成组:,,,,,.
甲学校学生成绩在这一组是:
乙学校学生成绩的平均数、中位数、众数、优秀率分及以上为优秀如下:
平均数 中位数 众数 优秀率
根据以上信息,回答下列问题:
甲学校学生,乙学校学生的综合素质展示成绩同为分,这两人在本校学生中综合素质展示排名更靠前的是______填“”或“”;
根据上述信息,推断______学校综合素质展示的水平更高,理由为______至少从两个不同的角度说明推断的合理性.
若每所学校综合素质展示的前名学生将被选入志愿服务团队,预估甲学校分数至少达到______分的学生才可以入选.
年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取名学生进行测试,并把测试成绩单位:绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 频数
请根据图表中所提供的信息,完成下列问题:
表中______,______;
样本成绩的中位数落在______范围内;
请把频数分布直方图补充完整;
该校共有名学生,估计该学校学生立定跳远成绩在范围内的有多少人?
某校为了了解初一年级共名同学对环保知识的掌握情况,对他们进行了环保知识测试.现随机抽取甲、乙两班各名同学的测试成绩满分分进行整理分析,过程如下:
【收集数据】:
甲班名学生测试成绩分别为:,,,,,,,,,,,,,,.
乙班名学生测试成绩中的成绩如下:,,,,.
【整理数据】:
班级
甲
乙
【分析数据】:
班级 平均数 众数 中位数 方差
甲
乙
【应用数据】:
根据以上信息,填空:________,________;
若规定测试成绩分及其以上为优秀,请估计参加环保知识测试的名学生中成绩为优秀的学生共有多少人?
根据以上数据,你认为哪个班的学生环保知识测试的整体成绩较好?请说明理由一条理由即可.
某数学老师将本班学生的身高数据精确到厘米交给甲、乙两同学,要求他们各自独立地绘制一幅频数分布直方图,甲绘制的图如图所示,乙绘制的图如图所示.经检查确认,甲绘制的直方图是正确的,乙在整理数据与绘图过程中均有个别错误.
问该班学生有多少人?
某同学身高为厘米,他说:“我们班上比我高的人不超过”,他的说法正确吗?
请指出乙在整理数据或绘图过程中所存在的一个错误;
设该班学生身高数据的中位数为,试写出的值.
第二十四届冬季奥林匹克运动会将于年月日至月日在北京和张家口市举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
【收集数据】从甲、乙两校各随机抽取名学生,在这次竞赛中他的成绩如下:
甲
乙
【整理、描述数据】按如下分数段整理、描述这两组样本数据:
甲
乙
说明:优秀成绩为,良好成绩为,合格成绩为.
【分析数据】两组样本数据的平均分、中位数、众数如表所示:
学校 平均分 中位数 众数
甲
乙
其中______,______.
【得出结论】
小明同学说:“这次竞赛我得了分,在我们学校排名属中游略偏上”由表中数据可知小明是______填“甲”或“乙”校的学生.
根据以上数据,请估计甲、乙两个学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生各有多少人?
根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.至少从两个不同的角度说明推断的合理性
某校学生会组织的为“社区扶贫对象”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为::::又知此次调查中捐款元的学生一共人.
某校调查的这组学生共有______人;
这组数据的众数是______元;中位数是______元;
若该校有名学生,都进行了捐款,估计全校学生共捐款多少元?
为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是______填“方案一”、“方案二”或“方案三”
学校根据样本数据,绘制成下表分及以上为“优秀”,分及以上为“及格”:
样本容量 平均分 及格率 优秀率 最高分 最低分
分数段统计学生成绩记为
分数段
频数
请结合表中信息解答下列问题:
估计该校名学生竞赛成绩的中位数落在哪个分数段内;
估计该校名学生中达到“优秀”的学生总人数.
国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
国家创新指数得分的频数分布直方图数据分成组:,,,,,,;
国家创新指数得分在这一组的是:
、、、、、、、、
个国家的人均国内生产总值和国家创新指数得分情况统计图:
中国的国家创新指数得分为.
以上数据来源于国家创新指数报告根据以上信息,回答下列问题:
中国的国家创新指数得分排名世界第______;
在个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线的上方,请在图中用“”圈出代表中国的点;
在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为______万美元;结果保留一位小数
下列推断合理的是______.
相比于点,所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
相比于点,所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗日标,进一步提高人均国内生产总值.
答案和解析
1.【答案】
【解析】解:、掷一个质地均匀的正六面体骰子,向上的面点数是的概率为,故A符合题意;
B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是:;故B不符合题意;
C、暗箱中有个红球和个黄球,它们只有颜色上的区别,从中任取一球是黄球的概率为,故C不符合题意;
D、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为,故D不符合题意.
故选:.
根据统计图可知,试验结果在附近波动,即其概率,计算四个选项的概率,约为者即为正确答案.
此题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率所求情况数与总情况数之比.同时此题在解答中要用到概率公式.
2.【答案】
【解析】解:由直方图可知:有桌顾客等位时间在至分钟,不能说是分钟,故A选项错误;
B.平均等位时间:
,故B选项错误;
C.因为样本容量是,中位数落在之间,故C选项错误;
D.分钟以上的人数为,故D选项正确.
故选:.
观察频数分布直方图,获取信息,然后逐一进行判断即可.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
3.【答案】
【解析】解:件
故选:.
求出总合格率,次品率,进而求出次品数量,对照做出选择.
考查频数分布表的意义,合格率的计算方法,从统计表中获取数据和数据之间的关系是解决问题的关键.
4.【答案】
【解析】解:.
故表中的值为,是合理推断;
,
,
,
故表中的值可以为,是不合理推断;
,
故这天的日均可回收物回收量的中位数在组,是合理推断;
,
故这天的日均可回收物回收量的平均数不低于,是合理推断.
故选:.
根据数据总和频数频率,列式计算可求的值;
根据组的频率满足,可求该范围的频数,进一步得到的值的范围,从而求解;
根据中位数的定义即可求解;
根据加权平均数的计算公式即可求解.
考查频数率分布表,从表中获取数量及数量之间的关系是解决问题的关键.
5.【答案】
【解析】
【分析】
本题主要考查的是组数的计算,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数最大值最小值组距计算,注意小数部分要进位,不要舍去.据此解答即可.
【解答】
解:在样本数据中最大值为,最小值为,
它们的差是,已知组距为,
那么由于,故可以分成组.
故选A.
6.【答案】
【解析】略
7.【答案】
【解析】A. 频率稳定在,不合题意
B. 频率稳定在,符合题意
C. 频率稳定在,不合题意
D. 频率稳定在,不合题意.
8.【答案】
【解析】解:由图形可知,从左到右的小矩形的高度比是::::,且总数为,
所以分数在之间的人数是人.
故选B.
由频数分布直方图上的小长方形的高为频数,知道高度比,即可算出每组的频率,再根据数据总数,即可求出每组对应的频数.
本题主要考查学生对频数直方图的认识和对频数的计算.
9.【答案】
【解析】解:参加本次竞赛的学生共有人,此项错误;
第五组的百分比为,此项正确;
成绩在分的人数最多,此项正确;
分以上的学生有名,此项错误;
故选:.
根据频数分布直方图逐项分析即可.
本题考查的是频数分布直方图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
10.【答案】
【解析】解:由频数分布直方图知,每周课外阅读时间不小于小时的人数是人,
故选:.
将课外阅读时间在小时和小时的人数相加即可得.
本题考查频数分布直方图,解题的关键是明确题意,利用数形结合的思想解答.
11.【答案】
【解析】解:在样本数据中最大值为,最小值为,它们的差是,已知组距为,那么由于,
故可以分成组.
故选A.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
12.【答案】
【解析】解:小文此次调查的小区居民的人数为位,此结论正确;
由频数直方图知,每周使用时间不足分钟的人数与分钟的人数相同,均为人,此结论错误;
每周使用时间超过分钟的人数占调查总人数的比例为,此结论错误;
每周使用时间在分钟的人数最多,有人,此结论正确;
故选:.
根据直方图表示的意义求得统计的总人数,以及每组的人数即可判断.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.【答案】
【解析】解:极差为,
,
可以分成组,
故答案为:.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
14.【答案】
【解析】解:将这个省、直辖市、自治区分配扶贫资金额度从小到大排列后处在中间位置的两个数的平均数为亿元,因此中位数是亿元,
故A说法正确;
由频数分布直方图可知,的有个省,的有个省,的有个省,而亿元在且只有个省,因此它位于第六名;
故B说法正确;
由统计图可知,年,中央财政脱贫专项资金对自治区的分配额度逐年增加,故C说法正确;
由两个自治区年中央财政脱贫专项资金变化情况的折线统计图可直观得到,自治区的比自治区的变化、波动要大,所以中央财政脱贫专项资金对自治区的分配额度比对自治区的稳定,故D说法错误.
故答案为:.
A.根据中位数的意义求解即可;
B.根据各组的频数可得答案;
C.根据折线统计图可得答案;
D.根据两个自治区年中央财政脱贫专项资金的变化情况的折线统计图可直观得到,自治区的比自治区的变化、波动要大,可得答案;
本题考查频数分布直方图、折线统计图,理解两个统计图中数量之间的关系是解决问题的关键.
15.【答案】
【解析】解:由表知,早高峰期间,乘坐线路“用时不超过分钟”的概率为,
线路分钟之内到达学校的概率为,线路分钟之内到达学校的概率为,
若要在分钟之内到达学校,应尽量选择乘坐线路,
故答案为:,.
用乘坐线路“用时不超过分钟”的班次数量除以总数量即可得出答案;先结合表中数据得出两线路分钟之内到达学校的概率,从而得出答案.
本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
16.【答案】
【解析】解:在这次测试中,成绩为及格分以上,不含分的在全班学生成绩中所占百分比为,
故答案为:.
用第、、、组的频数除以总人数即可得出答案.
本题主要考查频数分布直方图,解题的关键是根据频数分布直方图得出解题所需数据.
17.【答案】
【解析】解:在样本数据中最大值与最小值的差为,
又组距为,
组数,
应该分成组.
故答案为:.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
18.【答案】;
乙; 与甲校相比,乙校的中位数更高,说明乙校综合展示水平较高的同学更多;与甲校相比,乙校的优秀率更高,说明乙校综合展示水平高分的人数更多;
.
【解析】
解:甲学校学生成绩的中位数为,
乙学校学生成绩的中位数为,
故这两人在本校学生中综合素质展示排名更靠前的是,
故答案为:;
根据上述信息,推断乙学校综合素质展示的水平更高,理由为:与甲校相比,乙校的中位数更高,说明乙校综合展示水平较高的同学更多;与甲校相比,乙校的优秀率更高,说明乙校综合展示水平高分的人数更多;
故答案为:乙学校,与甲校相比,乙校的中位数更高,说明乙校综合展示水平较高的同学更多;与甲校相比,乙校的优秀率更高,说明乙校综合展示水平高分的人数更多
,
故甲学校分数至少达到分的学生才可以入选,
故答案为:.
【分析】
求得甲校的中位数即可得到结论;
根据频数分布直方图和表中信息即可得到结论;
求得每所学校被取了名学生的综合素质展示的前名学生将被选入志愿服务团队,于是得到结论.
本题考查频数分布直方图,中位数,平均数,众数的定义,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.【答案】解:,;
;
补全频数分布直方图如图所示:
人,
答:该校名学生中立定跳远成绩在范围内的有人.
【解析】
【分析】
本题考查频数分布表、频数分布直方图的意义和制作方法,理解各个数量之间的关系是正确解答的关键.
由频数分布直方图可得,由频数之和为求出的值;
根据中位数的意义,找出第、位的两个数落在哪个范围即可;
由的值即可补全频数分布直方图;
样本估计总体,样本中立定跳远成绩在范围内的占,因此估计总体人的是立定跳远成绩在范围内的人数.
【解答】
解:由统计图得,,,
故答案为:,;
由中位数的意义可得,个数据从小到大排列处在中间位置的两个数在组内,
故答案为:;
见答案;
见答案.
20.【答案】, ;
人,
即名学生中成绩为优秀的学生共有人;
甲班的学生掌握环保知识的整体水平较好,理由如下:
甲班的方差乙班的方差,甲班的平均分乙班的平均分
甲班的学生掌握环保相关知识的整体水平较好.
【解析】
【分析】
本题考查了频数率分布表,众数,中位数,正确的理解题意是解题的关键.
根据众数和中位数的定义求解可得;
用总人数乘以样本中优秀人数所占比例可得;
比较甲、乙两班的方差,再根据方差的意义即可得出答案.
【解答】
解:甲班出现次数最多,
众数是,则;
把乙班这组数按从小到大排列,则中位数是第个数,
即中位数出现在这一组中,故;
故答案为;.
见答案;
见答案.
;
根据题意得:
人,
答:成绩为优秀的学生共人.
21.【答案】解:
该班学生有人;
从图中得到高于厘米的人数为人,
,
他的说法正确;
如:在整理数据时,漏了一个数据,这个数据落在范围内或总人数少人;
由于总人数为人,则中位数应为第人与第的身高的平均数,落在了,
取组中值为.
【解析】根据频数分布直方图中每一组内的频数总和等于总数据个数,可得到本次随机抽查的学生人数;
计算高于厘米的人数的频率,就能说明他的说法是正确的;
详细观察图表可知:在整理数据时,漏了一个数据,这个数据落在范围内或总人数少人等,只要合理即可;
根据中位数的概念计算该班学生身高数据的中位数.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
22.【答案】 甲
【解析】解:【分析数据】甲校的名同学的成绩按照从小到大的顺序排列,第个和第个数据都是,
中位数为,即;
乙校的名同学的成绩中分出现次数最多,
众数为分,即;
【得出结论】甲校的中位数为分,小明同学的成绩高于此学校的中位数,
由表中数据可知小明是甲校的学生;
人,
人.
故估计甲学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生有人,估计乙学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生有人;
乙校的平均分高于甲校的平均分,且乙校的中位数高于甲校的中位数,说明乙校分数不低于分的人数比甲校多,
乙校的成绩较好.
故答案为:,;甲.
【分析数据】由原始数据根据中位数和众数的概念可得;
【得出结论】根据两个学校成绩的中位数判断可得;
先分别求出甲、乙两个学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生的概率,再乘总人数可得;
根据平均数和中位数这两方面的意义解答可得.
本题考查了频数率分布表,众数、中位数以及平均数,掌握众数、中位数以及平均数的定义是解题的关键.
23.【答案】
【解析】解:设捐元、元、元、元和元的人数分别为、、、、,
,
解得,
人,
故答案为:;
捐元、元、元、元和元的人数分别为,,,,,
出现次数最多,
众数为元;
共有个数据,第个和第个数据落在第四组内,
中位数为元;
故答案为:、;
元,
估算全校学生共捐款元.
利用从左到右各长方形高度之比为::::,可设捐元、元、元、元和元的人数分别为、、、、,则根据题意得,解得,然后计算即可;
先确定各组的人数,然后根据中位数和众数的定义求解;
先计算出样本的加权平均数,然后利用样本平均数估计总体,用乘以样本平均数即可.
本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.也考查了样本估计总体、中位数与众数.
24.【答案】解:方案三;
样本人中,成绩从小到大排列后,处在中间位置的两个数都在,
因此中位数在组中;
由题意得,人,
答:该校名学生中达到“优秀”的有人.
【解析】
【分析】
本题考查平均数、中位数的意义和计算方法,样本估计总体是统计中常用的方法.
根据抽样的代表性、普遍性和可操作性可知,方案三符合题意;
根据样本的中位数,估计总体中位数所在的范围;
样本中“优秀”人数占调查人数的,因此估计总体人的是“优秀”.
【解答】
解:根据抽样的代表性、普遍性和可操作性可得,方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析,是最符合题意的.
故答案为方案三;
见答案;
见答案.
25.【答案】解:;
如图所示:
;
.
【解析】本题考查了频数分布直方图、统计图、近似数等知识;读懂频数分布直方图和统计图是解题的关键.
国家创新指数得分为以上含的国家有个,
国家创新指数得分排名前的国家中,中国的国家创新指数得分排名世界第,
故答案为:;
如图所示:
由个国家的人均国内生产总值和国家创新指数得分情况统计图可知,在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为万美元;
故答案为:;
由个国家的人均国内生产总值和国家创新指数得分情况统计图可知,
相比于点、所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;合理;
相比于点,所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗日标,进一步提高人均国内生产总值;合理;
故答案为:.
第10页,共28页
第11页,共28页
6.3频数直方图同步练习
青岛版初中数学九年级下册
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
一、选择题
某小组作“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是
A. 掷一个质地均匀的正六面体骰子,向上的面点数是
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有个红球和个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
某餐厅规定等位时间达到分钟包括分钟可享受优惠现统计了某时段顾客的等位时间分钟,如图是根据数据绘制的统计图下列说法正确的是
A. 此时段有桌顾客等位时间是分钟
B. 此时段平均等位时间小于分钟
C. 此时段等位时间的中位数可能是
D. 此时段有桌顾客可享受优惠
对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频数表如下:
抽取件数件
合格频数
若出售件衬衣,则其中的次品最接近件.
A. B. C. D.
生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解年某市第二季度日均可回收物回收量情况,随机抽取该市年第二季度的天数据,整理后绘制成统计表进行分析.
日均可回收物回收量千吨 合计
频数
频率
表中组的频率满足.
下面有四个推断:
表中的值为;
表中的值可以为;
这天的日均可回收物回收量的中位数在组;
这天的日均可回收物回收量的平均数不低于.
所有合理推断的序号是
A. B. C. D.
一个容量为的样本最大值为,最小值为,取组距为,则可以分成
A. 组 B. 组 C. 组 D. 组
某学校为了了解该学校七年级学生双休日上网的情况,随机调查了该学校七年级的名学生,得到了上周双休日上网时间的一组样本数据,其频数分布直方图如图所示,那么估计该学校七年级每名学生双休日上网的平均时间是
A. 小时 B. 小时 C. 小时 D. 小时
甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的折线统计图如图所示,符合这一结果的试验可能是
A. 掷一枚质地均匀的骰子,出现点朝上的频率
B. 任意写一个正整数,它能被整除的频率
C. 抛一枚硬币,出现正面朝上的频率
D. 从一个装有个白球和个红球的袋子中任取一球,取到白球的频率
某班有位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数分布直方图横半轴表示分数,把分到分之间的分数分成组,组距是分,纵半轴表示频数如图所示,从左到右的小矩形的高度比是::::,则由图可知,其中分数在之间的人数是
A. B. C. D.
某校组织部分学生参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是,,,,第五组的频数是则:
参加本次竞赛的学生共有人;
第五组的百分比为;
成绩在分的人数最多;
分以上的学生有名;
其中正确的个数有
A. 个 B. 个 C. 个 D. 个
如图,是九班名同学每周课外阅读时间的频数分布直方图每组含前一个边界值,不含后一个边界值,由图可知,每周课外阅读时间不小于小时的人数是
A. 人 B. 人 C. 人 D. 人
统计得到的一组数据有个,其中最大值为,最小值为,取组距为,可以分成
A. 组 B. 组 C. 组 D. 组
小文同学统计了某小区部分居民每周使用共享单车的时间,并绘制了统计图,如图所示.下面有四个推断:
小文此次一共调查了位小区居民;
每周使用时间不足的人数多于的人数;
每周使用时间超过的人数超过调查总人数的一半;
每周使用时间在的人数最多.
根据图中信息,上述说法中正确的是
A. B. C. D.
二、填空题
一个样本最大值为,最小值为,取组距为,则可以分成______组.
为了打赢“脱贫攻坚”战役,国家设立了“中央财政脱贫专项资金”以保证对各省贫困地区的持续投入.小莹同学通过登陆国家乡村振兴局网站,查询到了年中央财政脱贫专项资金对个省份的分配额度亿元,并对数据进行整理和分析.图是反映年中央财政脱贫专项资金分配额度的频数分布直方图,且在这一组分配的额度分别是:,,,,,,,,图是反映年中央财政脱贫专项资金对自治区和自治区的分配额度变化折线图.则下列说法中正确的是______.
A.年,中央财政脱贫专项资金对各省份的分配额度的中位数为亿元
B.年,某省获得的分配额度为亿元,该额度在个省份中由高到低排第六名
C.年,中央财政脱贫专项资金对自治区的分配额度逐年增加
D.年,中央财政脱贫专项资金对自治区的分配额度比对自治区的稳定
小夏同学从家到学校有,两条不同的公交线路为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了个班次的公交车,收集了这些班次的公交车用时单位:分钟的数据,统计如下:
公交车用时频数
公交车线 合计
据此估计,早高峰期间,乘坐线路“用时不超过分钟”的概率为______ ;若要在分钟之内到达学校,应尽量选择乘坐______ 填或线路.
对某班最近一次数学测试成绩得分取整数进行统计分析,全班共人,将分以上不含分的成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为及格分以上,不含分的在全班学生成绩中所占百分比为______ .
有个数据,其中最大值为,最小值为,若取组距为,则应该分成______组.
三、解答题
为迎接年冬奥会,鼓励更多的学生参与到志愿服务中学,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有名学生进入综合素质展开环节,为了了解两所学校这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了名学生的综合素质展示成绩百分制,并对数据成绩进行整理、描述和分析,下面给出了部分信息.
甲学校学生成绩的频数分布直方图如下数据分成组:,,,,,.
甲学校学生成绩在这一组是:
乙学校学生成绩的平均数、中位数、众数、优秀率分及以上为优秀如下:
平均数 中位数 众数 优秀率
根据以上信息,回答下列问题:
甲学校学生,乙学校学生的综合素质展示成绩同为分,这两人在本校学生中综合素质展示排名更靠前的是______填“”或“”;
根据上述信息,推断______学校综合素质展示的水平更高,理由为______至少从两个不同的角度说明推断的合理性.
若每所学校综合素质展示的前名学生将被选入志愿服务团队,预估甲学校分数至少达到______分的学生才可以入选.
年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取名学生进行测试,并把测试成绩单位:绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 频数
请根据图表中所提供的信息,完成下列问题:
表中______,______;
样本成绩的中位数落在______范围内;
请把频数分布直方图补充完整;
该校共有名学生,估计该学校学生立定跳远成绩在范围内的有多少人?
某校为了了解初一年级共名同学对环保知识的掌握情况,对他们进行了环保知识测试.现随机抽取甲、乙两班各名同学的测试成绩满分分进行整理分析,过程如下:
【收集数据】:
甲班名学生测试成绩分别为:,,,,,,,,,,,,,,.
乙班名学生测试成绩中的成绩如下:,,,,.
【整理数据】:
班级
甲
乙
【分析数据】:
班级 平均数 众数 中位数 方差
甲
乙
【应用数据】:
根据以上信息,填空:________,________;
若规定测试成绩分及其以上为优秀,请估计参加环保知识测试的名学生中成绩为优秀的学生共有多少人?
根据以上数据,你认为哪个班的学生环保知识测试的整体成绩较好?请说明理由一条理由即可.
某数学老师将本班学生的身高数据精确到厘米交给甲、乙两同学,要求他们各自独立地绘制一幅频数分布直方图,甲绘制的图如图所示,乙绘制的图如图所示.经检查确认,甲绘制的直方图是正确的,乙在整理数据与绘图过程中均有个别错误.
问该班学生有多少人?
某同学身高为厘米,他说:“我们班上比我高的人不超过”,他的说法正确吗?
请指出乙在整理数据或绘图过程中所存在的一个错误;
设该班学生身高数据的中位数为,试写出的值.
第二十四届冬季奥林匹克运动会将于年月日至月日在北京和张家口市举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
【收集数据】从甲、乙两校各随机抽取名学生,在这次竞赛中他的成绩如下:
甲
乙
【整理、描述数据】按如下分数段整理、描述这两组样本数据:
甲
乙
说明:优秀成绩为,良好成绩为,合格成绩为.
【分析数据】两组样本数据的平均分、中位数、众数如表所示:
学校 平均分 中位数 众数
甲
乙
其中______,______.
【得出结论】
小明同学说:“这次竞赛我得了分,在我们学校排名属中游略偏上”由表中数据可知小明是______填“甲”或“乙”校的学生.
根据以上数据,请估计甲、乙两个学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生各有多少人?
根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.至少从两个不同的角度说明推断的合理性
某校学生会组织的为“社区扶贫对象”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为::::又知此次调查中捐款元的学生一共人.
某校调查的这组学生共有______人;
这组数据的众数是______元;中位数是______元;
若该校有名学生,都进行了捐款,估计全校学生共捐款多少元?
为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是______填“方案一”、“方案二”或“方案三”
学校根据样本数据,绘制成下表分及以上为“优秀”,分及以上为“及格”:
样本容量 平均分 及格率 优秀率 最高分 最低分
分数段统计学生成绩记为
分数段
频数
请结合表中信息解答下列问题:
估计该校名学生竞赛成绩的中位数落在哪个分数段内;
估计该校名学生中达到“优秀”的学生总人数.
国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
国家创新指数得分的频数分布直方图数据分成组:,,,,,,;
国家创新指数得分在这一组的是:
、、、、、、、、
个国家的人均国内生产总值和国家创新指数得分情况统计图:
中国的国家创新指数得分为.
以上数据来源于国家创新指数报告根据以上信息,回答下列问题:
中国的国家创新指数得分排名世界第______;
在个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线的上方,请在图中用“”圈出代表中国的点;
在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为______万美元;结果保留一位小数
下列推断合理的是______.
相比于点,所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
相比于点,所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗日标,进一步提高人均国内生产总值.
答案和解析
1.【答案】
【解析】解:、掷一个质地均匀的正六面体骰子,向上的面点数是的概率为,故A符合题意;
B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是:;故B不符合题意;
C、暗箱中有个红球和个黄球,它们只有颜色上的区别,从中任取一球是黄球的概率为,故C不符合题意;
D、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为,故D不符合题意.
故选:.
根据统计图可知,试验结果在附近波动,即其概率,计算四个选项的概率,约为者即为正确答案.
此题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率所求情况数与总情况数之比.同时此题在解答中要用到概率公式.
2.【答案】
【解析】解:由直方图可知:有桌顾客等位时间在至分钟,不能说是分钟,故A选项错误;
B.平均等位时间:
,故B选项错误;
C.因为样本容量是,中位数落在之间,故C选项错误;
D.分钟以上的人数为,故D选项正确.
故选:.
观察频数分布直方图,获取信息,然后逐一进行判断即可.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
3.【答案】
【解析】解:件
故选:.
求出总合格率,次品率,进而求出次品数量,对照做出选择.
考查频数分布表的意义,合格率的计算方法,从统计表中获取数据和数据之间的关系是解决问题的关键.
4.【答案】
【解析】解:.
故表中的值为,是合理推断;
,
,
,
故表中的值可以为,是不合理推断;
,
故这天的日均可回收物回收量的中位数在组,是合理推断;
,
故这天的日均可回收物回收量的平均数不低于,是合理推断.
故选:.
根据数据总和频数频率,列式计算可求的值;
根据组的频率满足,可求该范围的频数,进一步得到的值的范围,从而求解;
根据中位数的定义即可求解;
根据加权平均数的计算公式即可求解.
考查频数率分布表,从表中获取数量及数量之间的关系是解决问题的关键.
5.【答案】
【解析】
【分析】
本题主要考查的是组数的计算,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.根据组数最大值最小值组距计算,注意小数部分要进位,不要舍去.据此解答即可.
【解答】
解:在样本数据中最大值为,最小值为,
它们的差是,已知组距为,
那么由于,故可以分成组.
故选A.
6.【答案】
【解析】略
7.【答案】
【解析】A. 频率稳定在,不合题意
B. 频率稳定在,符合题意
C. 频率稳定在,不合题意
D. 频率稳定在,不合题意.
8.【答案】
【解析】解:由图形可知,从左到右的小矩形的高度比是::::,且总数为,
所以分数在之间的人数是人.
故选B.
由频数分布直方图上的小长方形的高为频数,知道高度比,即可算出每组的频率,再根据数据总数,即可求出每组对应的频数.
本题主要考查学生对频数直方图的认识和对频数的计算.
9.【答案】
【解析】解:参加本次竞赛的学生共有人,此项错误;
第五组的百分比为,此项正确;
成绩在分的人数最多,此项正确;
分以上的学生有名,此项错误;
故选:.
根据频数分布直方图逐项分析即可.
本题考查的是频数分布直方图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
10.【答案】
【解析】解:由频数分布直方图知,每周课外阅读时间不小于小时的人数是人,
故选:.
将课外阅读时间在小时和小时的人数相加即可得.
本题考查频数分布直方图,解题的关键是明确题意,利用数形结合的思想解答.
11.【答案】
【解析】解:在样本数据中最大值为,最小值为,它们的差是,已知组距为,那么由于,
故可以分成组.
故选A.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
12.【答案】
【解析】解:小文此次调查的小区居民的人数为位,此结论正确;
由频数直方图知,每周使用时间不足分钟的人数与分钟的人数相同,均为人,此结论错误;
每周使用时间超过分钟的人数占调查总人数的比例为,此结论错误;
每周使用时间在分钟的人数最多,有人,此结论正确;
故选:.
根据直方图表示的意义求得统计的总人数,以及每组的人数即可判断.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.【答案】
【解析】解:极差为,
,
可以分成组,
故答案为:.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
14.【答案】
【解析】解:将这个省、直辖市、自治区分配扶贫资金额度从小到大排列后处在中间位置的两个数的平均数为亿元,因此中位数是亿元,
故A说法正确;
由频数分布直方图可知,的有个省,的有个省,的有个省,而亿元在且只有个省,因此它位于第六名;
故B说法正确;
由统计图可知,年,中央财政脱贫专项资金对自治区的分配额度逐年增加,故C说法正确;
由两个自治区年中央财政脱贫专项资金变化情况的折线统计图可直观得到,自治区的比自治区的变化、波动要大,所以中央财政脱贫专项资金对自治区的分配额度比对自治区的稳定,故D说法错误.
故答案为:.
A.根据中位数的意义求解即可;
B.根据各组的频数可得答案;
C.根据折线统计图可得答案;
D.根据两个自治区年中央财政脱贫专项资金的变化情况的折线统计图可直观得到,自治区的比自治区的变化、波动要大,可得答案;
本题考查频数分布直方图、折线统计图,理解两个统计图中数量之间的关系是解决问题的关键.
15.【答案】
【解析】解:由表知,早高峰期间,乘坐线路“用时不超过分钟”的概率为,
线路分钟之内到达学校的概率为,线路分钟之内到达学校的概率为,
若要在分钟之内到达学校,应尽量选择乘坐线路,
故答案为:,.
用乘坐线路“用时不超过分钟”的班次数量除以总数量即可得出答案;先结合表中数据得出两线路分钟之内到达学校的概率,从而得出答案.
本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
16.【答案】
【解析】解:在这次测试中,成绩为及格分以上,不含分的在全班学生成绩中所占百分比为,
故答案为:.
用第、、、组的频数除以总人数即可得出答案.
本题主要考查频数分布直方图,解题的关键是根据频数分布直方图得出解题所需数据.
17.【答案】
【解析】解:在样本数据中最大值与最小值的差为,
又组距为,
组数,
应该分成组.
故答案为:.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
18.【答案】;
乙; 与甲校相比,乙校的中位数更高,说明乙校综合展示水平较高的同学更多;与甲校相比,乙校的优秀率更高,说明乙校综合展示水平高分的人数更多;
.
【解析】
解:甲学校学生成绩的中位数为,
乙学校学生成绩的中位数为,
故这两人在本校学生中综合素质展示排名更靠前的是,
故答案为:;
根据上述信息,推断乙学校综合素质展示的水平更高,理由为:与甲校相比,乙校的中位数更高,说明乙校综合展示水平较高的同学更多;与甲校相比,乙校的优秀率更高,说明乙校综合展示水平高分的人数更多;
故答案为:乙学校,与甲校相比,乙校的中位数更高,说明乙校综合展示水平较高的同学更多;与甲校相比,乙校的优秀率更高,说明乙校综合展示水平高分的人数更多
,
故甲学校分数至少达到分的学生才可以入选,
故答案为:.
【分析】
求得甲校的中位数即可得到结论;
根据频数分布直方图和表中信息即可得到结论;
求得每所学校被取了名学生的综合素质展示的前名学生将被选入志愿服务团队,于是得到结论.
本题考查频数分布直方图,中位数,平均数,众数的定义,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.【答案】解:,;
;
补全频数分布直方图如图所示:
人,
答:该校名学生中立定跳远成绩在范围内的有人.
【解析】
【分析】
本题考查频数分布表、频数分布直方图的意义和制作方法,理解各个数量之间的关系是正确解答的关键.
由频数分布直方图可得,由频数之和为求出的值;
根据中位数的意义,找出第、位的两个数落在哪个范围即可;
由的值即可补全频数分布直方图;
样本估计总体,样本中立定跳远成绩在范围内的占,因此估计总体人的是立定跳远成绩在范围内的人数.
【解答】
解:由统计图得,,,
故答案为:,;
由中位数的意义可得,个数据从小到大排列处在中间位置的两个数在组内,
故答案为:;
见答案;
见答案.
20.【答案】, ;
人,
即名学生中成绩为优秀的学生共有人;
甲班的学生掌握环保知识的整体水平较好,理由如下:
甲班的方差乙班的方差,甲班的平均分乙班的平均分
甲班的学生掌握环保相关知识的整体水平较好.
【解析】
【分析】
本题考查了频数率分布表,众数,中位数,正确的理解题意是解题的关键.
根据众数和中位数的定义求解可得;
用总人数乘以样本中优秀人数所占比例可得;
比较甲、乙两班的方差,再根据方差的意义即可得出答案.
【解答】
解:甲班出现次数最多,
众数是,则;
把乙班这组数按从小到大排列,则中位数是第个数,
即中位数出现在这一组中,故;
故答案为;.
见答案;
见答案.
;
根据题意得:
人,
答:成绩为优秀的学生共人.
21.【答案】解:
该班学生有人;
从图中得到高于厘米的人数为人,
,
他的说法正确;
如:在整理数据时,漏了一个数据,这个数据落在范围内或总人数少人;
由于总人数为人,则中位数应为第人与第的身高的平均数,落在了,
取组中值为.
【解析】根据频数分布直方图中每一组内的频数总和等于总数据个数,可得到本次随机抽查的学生人数;
计算高于厘米的人数的频率,就能说明他的说法是正确的;
详细观察图表可知:在整理数据时,漏了一个数据,这个数据落在范围内或总人数少人等,只要合理即可;
根据中位数的概念计算该班学生身高数据的中位数.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
22.【答案】 甲
【解析】解:【分析数据】甲校的名同学的成绩按照从小到大的顺序排列,第个和第个数据都是,
中位数为,即;
乙校的名同学的成绩中分出现次数最多,
众数为分,即;
【得出结论】甲校的中位数为分,小明同学的成绩高于此学校的中位数,
由表中数据可知小明是甲校的学生;
人,
人.
故估计甲学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生有人,估计乙学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生有人;
乙校的平均分高于甲校的平均分,且乙校的中位数高于甲校的中位数,说明乙校分数不低于分的人数比甲校多,
乙校的成绩较好.
故答案为:,;甲.
【分析数据】由原始数据根据中位数和众数的概念可得;
【得出结论】根据两个学校成绩的中位数判断可得;
先分别求出甲、乙两个学校在这次冬奥知识网上答题竞赛中成绩为优秀的学生的概率,再乘总人数可得;
根据平均数和中位数这两方面的意义解答可得.
本题考查了频数率分布表,众数、中位数以及平均数,掌握众数、中位数以及平均数的定义是解题的关键.
23.【答案】
【解析】解:设捐元、元、元、元和元的人数分别为、、、、,
,
解得,
人,
故答案为:;
捐元、元、元、元和元的人数分别为,,,,,
出现次数最多,
众数为元;
共有个数据,第个和第个数据落在第四组内,
中位数为元;
故答案为:、;
元,
估算全校学生共捐款元.
利用从左到右各长方形高度之比为::::,可设捐元、元、元、元和元的人数分别为、、、、,则根据题意得,解得,然后计算即可;
先确定各组的人数,然后根据中位数和众数的定义求解;
先计算出样本的加权平均数,然后利用样本平均数估计总体,用乘以样本平均数即可.
本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.也考查了样本估计总体、中位数与众数.
24.【答案】解:方案三;
样本人中,成绩从小到大排列后,处在中间位置的两个数都在,
因此中位数在组中;
由题意得,人,
答:该校名学生中达到“优秀”的有人.
【解析】
【分析】
本题考查平均数、中位数的意义和计算方法,样本估计总体是统计中常用的方法.
根据抽样的代表性、普遍性和可操作性可知,方案三符合题意;
根据样本的中位数,估计总体中位数所在的范围;
样本中“优秀”人数占调查人数的,因此估计总体人的是“优秀”.
【解答】
解:根据抽样的代表性、普遍性和可操作性可得,方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析,是最符合题意的.
故答案为方案三;
见答案;
见答案.
25.【答案】解:;
如图所示:
;
.
【解析】本题考查了频数分布直方图、统计图、近似数等知识;读懂频数分布直方图和统计图是解题的关键.
国家创新指数得分为以上含的国家有个,
国家创新指数得分排名前的国家中,中国的国家创新指数得分排名世界第,
故答案为:;
如图所示:
由个国家的人均国内生产总值和国家创新指数得分情况统计图可知,在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为万美元;
故答案为:;
由个国家的人均国内生产总值和国家创新指数得分情况统计图可知,
相比于点、所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;合理;
相比于点,所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗日标,进一步提高人均国内生产总值;合理;
故答案为:.
第10页,共28页
第11页,共28页
