人教版九年级上册数学24.4弧长与扇形面积-求弧长(word版、含答案)
文档属性
| 名称 | 人教版九年级上册数学24.4弧长与扇形面积-求弧长(word版、含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 418.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 00:00:00 | ||
图片预览


文档简介
人教版九年级上册数学24.4弧长与扇形面积-求弧长
一、单选题
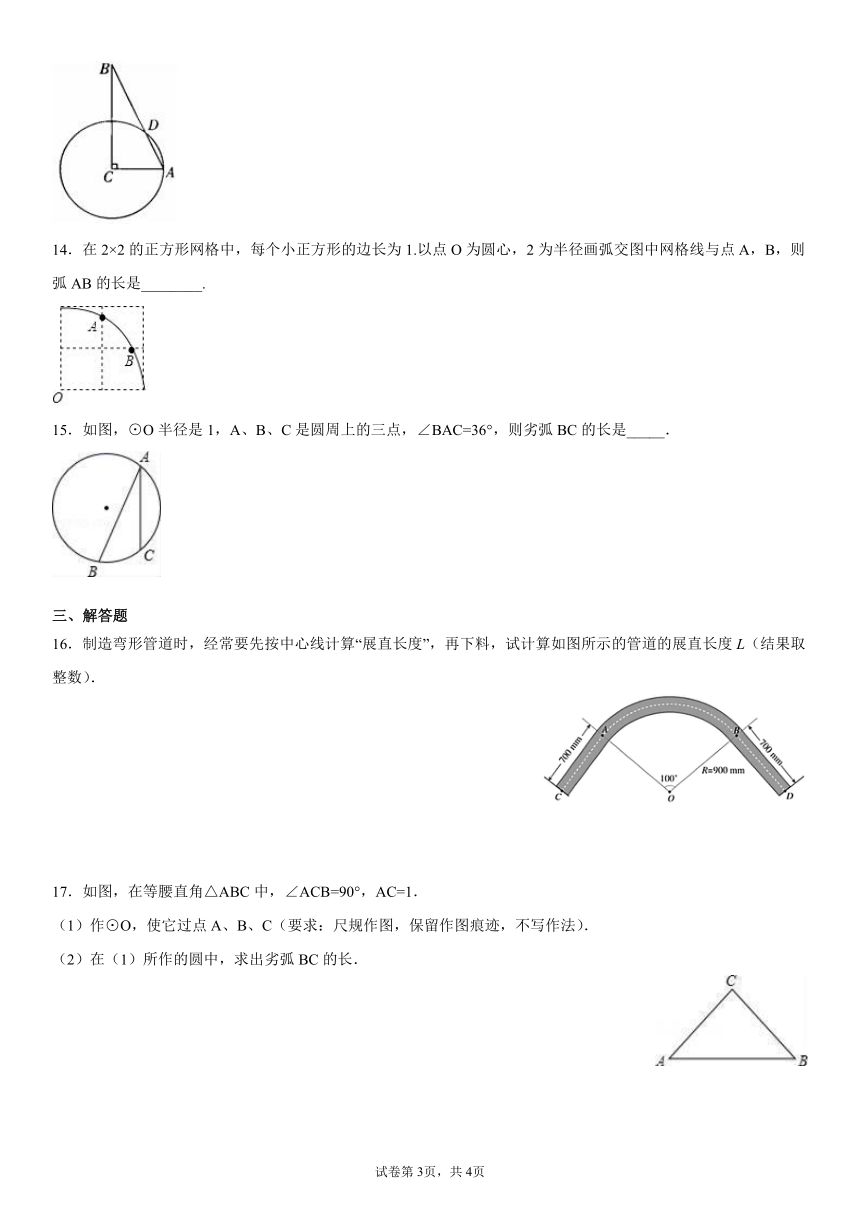
1.已知某扇形的半径为6,圆心角的度数为,则扇形的弧长为( )
A. B. C. D.
2.若半径为6的圆中,扇形面积为,则它的弧长为( ).
A. B. C. D.
3.如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为( )
A. B. C. D.
4.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则弧AC的长为( )
A.2π B.π C. D.
5.如图,在扇形中,为弦,,,,则的长为( )
A. B. C. D.
6.如图,菱形ABCD中,∠B=60°,AB=4,以AD为直径的⊙O交CD于点E,则的长为( )
A. B. C. D.
7.秋千拉绳长3米,静止时踩板离地面0.5米,一小朋友荡该秋千时, 秋千最高处踩板离地面2米(左,右对称),则该秋千所荡过的圆弧长为( )
A.米 B.2米 C.米 D.米
8.如图所示,小明从半径为的圆形纸片中剪下圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为( )
A. B. C. D.
二、填空题
9.半径为的圆中,的圆心角所对的弧长为__________;弧长为的圆心角约为________.
10.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
11.如图,在扇形中,半径与的夹角为,点与点的距离为,若扇形恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为______.
12.如图,过的顶点、、,且,,则弧长为________.
13.如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA为半径的圆交AB于D,若AC=6,则弧AD的长为_________.
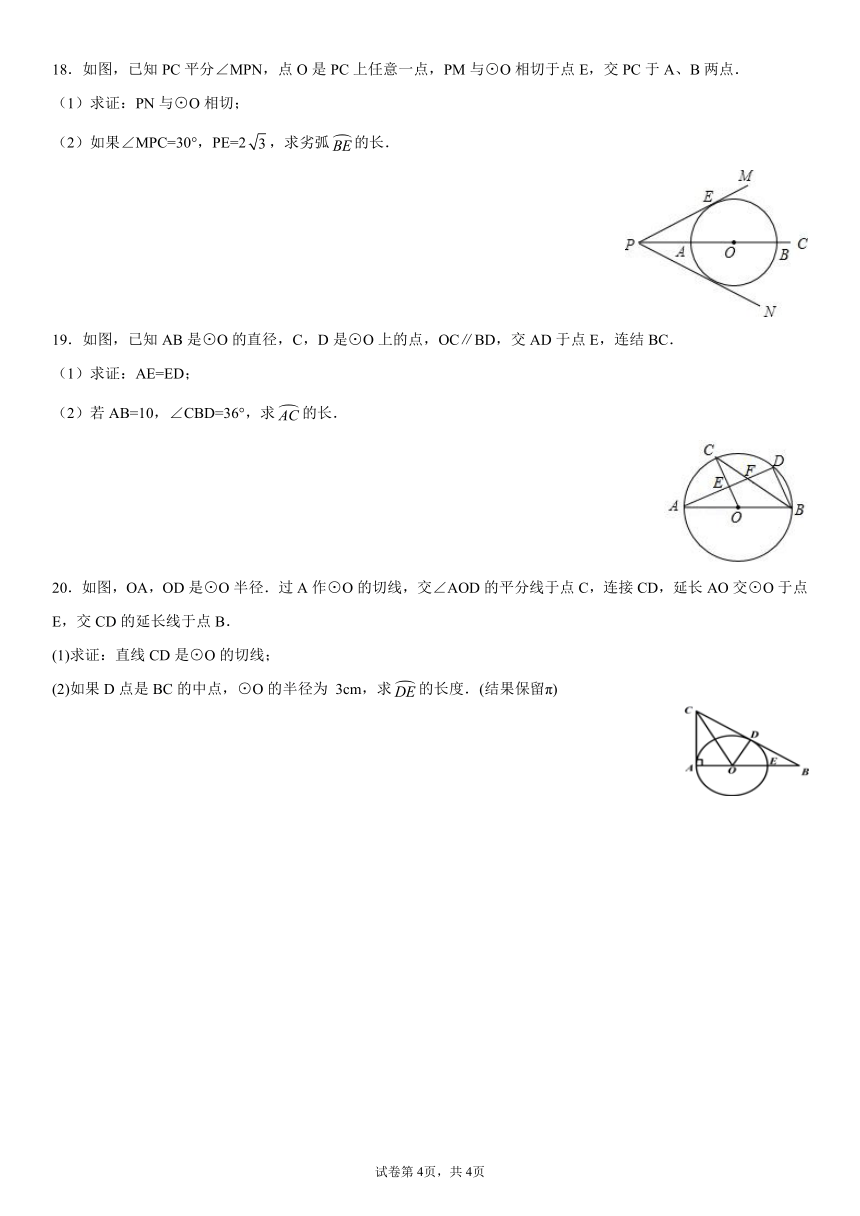
14.在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧交图中网格线与点A,B,则弧AB的长是________.
15.如图,⊙O半径是1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是_____.
三、解答题
16.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图所示的管道的展直长度L(结果取整数).
17.如图,在等腰直角△ABC中,∠ACB=90°,AC=1.
(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法).
(2)在(1)所作的圆中,求出劣弧BC的长.
18.如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
(1)求证:PN与⊙O相切;
(2)如果∠MPC=30°,PE=2,求劣弧的长.
19.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
20.如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求的长度.(结果保留π)
参考答案
1.C
2.B
3.D
4.B
5.B
6.B
7.B
8.C
9.
10.4π.
11.
12.
13.
14.
15.π.
16.
解:由弧长公式,得的长.
展直长度.
答:图中所示的管道的展直长度是2970mm.
17.
解:(1)如图,作线段AB的垂直平分线交AB于O点,然后以O为圆心,OA为半径画圆,⊙O即为所作;
(2)∵在等腰直角△ABC中,∠ACB=90°,AC=1,
∴AB=AC=,
∵线段AB的垂直平分线交AB于O点,
∴∠BOC=90°,OB=OA=AB=,
∴劣弧BC的长=π.
18.
解:(1)连接OE,过O作OF⊥PN,如图所示,
∵PM与圆O相切,
∴OE⊥PM,
∴∠OEP=∠OFP=90°,
∵PC平分∠MPN,
∴∠EPO=∠FPO,
在△PEO和△PFO中,
∵∠EPO=∠FPO,∠OEP=∠OFP,OP=OP,
∴△PEO≌△PFO(AAS),
∴OF=OE,则PN与圆O相切;
(2)在Rt△EPO中,∠MPC=30°,PE=,
∴∠EOP=60°,OE=2,
∴∠EOB=120°,
则的长l==.
考点:1.切线的判定与性质;2.弧长的计算.
19.
详证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED;
(2)∵OC⊥AD,
∴ ,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴ =.
20.
(1)证明:∵AC是⊙O切线,
∴OA⊥AC,
∴∠OAC=90°,
∵CO平分∠AOD,
∴∠AOC=∠COD,
在△AOC和△DOC中,
∴△AOC≌△DOC,
∴∠ODC=∠OAC=90°,
∴OD⊥CD,
∴直线CD是⊙O的切线.
(2)∵OD⊥BC,DC=DB,
∴OC=OB,
∴∠OCD=∠B=∠ACO,
∵∠B+∠ACB=90°,
∴∠B=30°,∠DOE=60°,
∴的长度=π.
试卷第2页,共4页
试卷第1页,共4页
一、单选题
1.已知某扇形的半径为6,圆心角的度数为,则扇形的弧长为( )
A. B. C. D.
2.若半径为6的圆中,扇形面积为,则它的弧长为( ).
A. B. C. D.
3.如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面周长为( )
A. B. C. D.
4.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则弧AC的长为( )
A.2π B.π C. D.
5.如图,在扇形中,为弦,,,,则的长为( )
A. B. C. D.
6.如图,菱形ABCD中,∠B=60°,AB=4,以AD为直径的⊙O交CD于点E,则的长为( )
A. B. C. D.
7.秋千拉绳长3米,静止时踩板离地面0.5米,一小朋友荡该秋千时, 秋千最高处踩板离地面2米(左,右对称),则该秋千所荡过的圆弧长为( )
A.米 B.2米 C.米 D.米
8.如图所示,小明从半径为的圆形纸片中剪下圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为( )
A. B. C. D.
二、填空题
9.半径为的圆中,的圆心角所对的弧长为__________;弧长为的圆心角约为________.
10.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
11.如图,在扇形中,半径与的夹角为,点与点的距离为,若扇形恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为______.
12.如图,过的顶点、、,且,,则弧长为________.
13.如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA为半径的圆交AB于D,若AC=6,则弧AD的长为_________.
14.在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧交图中网格线与点A,B,则弧AB的长是________.
15.如图,⊙O半径是1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是_____.
三、解答题
16.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算如图所示的管道的展直长度L(结果取整数).
17.如图,在等腰直角△ABC中,∠ACB=90°,AC=1.
(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法).
(2)在(1)所作的圆中,求出劣弧BC的长.
18.如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
(1)求证:PN与⊙O相切;
(2)如果∠MPC=30°,PE=2,求劣弧的长.
19.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
20.如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求的长度.(结果保留π)
参考答案
1.C
2.B
3.D
4.B
5.B
6.B
7.B
8.C
9.
10.4π.
11.
12.
13.
14.
15.π.
16.
解:由弧长公式,得的长.
展直长度.
答:图中所示的管道的展直长度是2970mm.
17.
解:(1)如图,作线段AB的垂直平分线交AB于O点,然后以O为圆心,OA为半径画圆,⊙O即为所作;
(2)∵在等腰直角△ABC中,∠ACB=90°,AC=1,
∴AB=AC=,
∵线段AB的垂直平分线交AB于O点,
∴∠BOC=90°,OB=OA=AB=,
∴劣弧BC的长=π.
18.
解:(1)连接OE,过O作OF⊥PN,如图所示,
∵PM与圆O相切,
∴OE⊥PM,
∴∠OEP=∠OFP=90°,
∵PC平分∠MPN,
∴∠EPO=∠FPO,
在△PEO和△PFO中,
∵∠EPO=∠FPO,∠OEP=∠OFP,OP=OP,
∴△PEO≌△PFO(AAS),
∴OF=OE,则PN与圆O相切;
(2)在Rt△EPO中,∠MPC=30°,PE=,
∴∠EOP=60°,OE=2,
∴∠EOB=120°,
则的长l==.
考点:1.切线的判定与性质;2.弧长的计算.
19.
详证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED;
(2)∵OC⊥AD,
∴ ,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴ =.
20.
(1)证明:∵AC是⊙O切线,
∴OA⊥AC,
∴∠OAC=90°,
∵CO平分∠AOD,
∴∠AOC=∠COD,
在△AOC和△DOC中,
∴△AOC≌△DOC,
∴∠ODC=∠OAC=90°,
∴OD⊥CD,
∴直线CD是⊙O的切线.
(2)∵OD⊥BC,DC=DB,
∴OC=OB,
∴∠OCD=∠B=∠ACO,
∵∠B+∠ACB=90°,
∴∠B=30°,∠DOE=60°,
∴的长度=π.
试卷第2页,共4页
试卷第1页,共4页
同课章节目录
