1.5全称量词与存在量词 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共20张PPT)
文档属性
| 名称 | 1.5全称量词与存在量词 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 21:07:06 | ||
图片预览







文档简介
(共20张PPT)
1.5 全称量词与存在量词
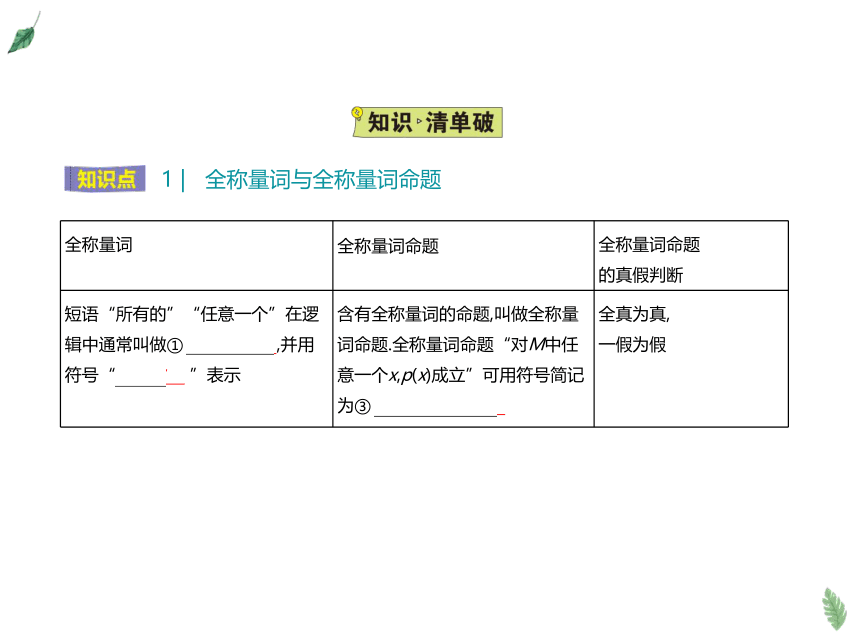
1 | 全称量词与全称量词命题
全称量词 全称量词命题 全称量词命题
的真假判断
短语“所有的”“任意一个”在逻辑中通常叫做① 全称量词 ,并用符号“② ”表示 含有全称量词的命题,叫做全称量词命题.全称量词命题“对M中任意一个x,p(x)成立”可用符号简记为③ x∈M,p(x) 全真为真,
一假为假
2 | 存在量词与存在量词命题
存在量词 存在量词命题 存在量词命题
的真假判断
短语“存在一个”“至少有一个”在逻辑中通常叫做④ 存在量词 ,并用符号“⑤ ”表示 含有存在量词的命题,叫做存在量词命题.存在量词命题“存在M中的元素x,p(x)成立”可用符号简记为⑥ x∈M,p(x) 一真为真,
全假为假
1.将一个命题的结论换成原来结论的反面,条件不变,得到一个新的命题,这个命
题就是原来命题的否定.如原来的命题为p:若s,则t,则它的否定为 p:⑦ 若s,则 t .
2.一个命题与它的否定不能同时为真,也不能同时为假,只能是⑧ 一真一假 .
3 | 命题的否定
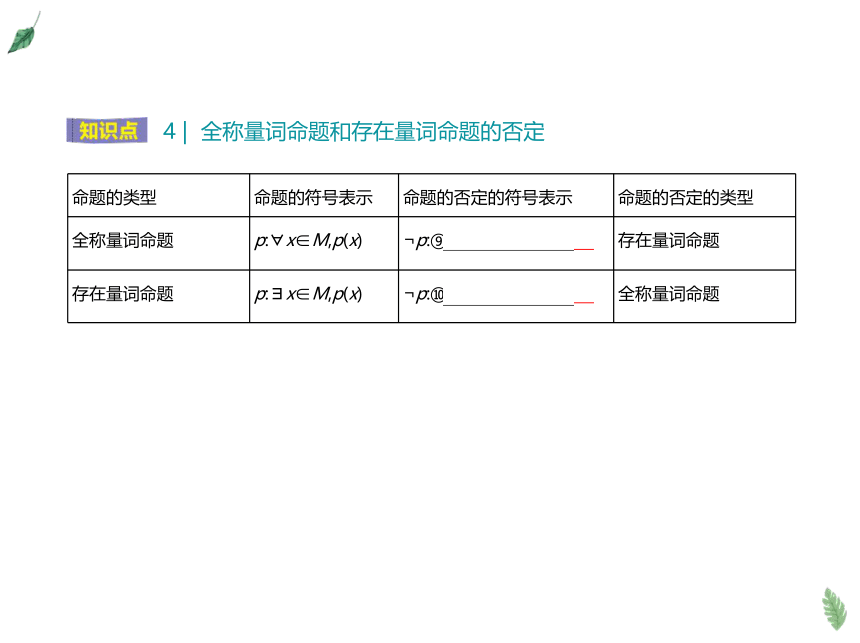
4 | 全称量词命题和存在量词命题的否定
命题的类型 命题的符号表示 命题的否定的符号表示 命题的否定的类型
全称量词命题 p: x∈M,p(x) p:⑨ x∈M, p(x) 存在量词命题
存在量词命题 p: x∈M,p(x) p:⑩ x∈M, p(x) 全称量词命题
1.“有些”“有一个”“有的”是存在量词. ( √ )
2.全称量词命题“自然数都是正整数”是真命题. ( )
提示:0是自然数,但0不是正整数,因此“自然数都是正整数”是假命题.
3.在全称量词命题和存在量词命题中,量词都可以省略. ( )
提示:在存在量词命题中,量词不能省略,有些全称量词命题的量词可以省略.
4.命题p:“ x∈M,p(x)”的否定是“ x∈M, p(x)”,它们可以同真同假. ( )
5.若命题 p是存在量词命题,则命题p是全称量词命题.( √ )
6.用自然语言描述的全称量词命题的否定形式是唯一的.( )
提示:用自然语言描述的全称量词命题的否定形式并不唯一,如“所有的菱形都
是平行四边形”,它的否定可以是“并不是所有的菱形都是平行四边形”,也可
以是“有些菱形不是平行四边形”.
判断正误,正确的画“ √” ,错误的画“ ” .
1 | 全称量词命题、存在量词命题及其否定的真假判断
哥德巴赫猜想是世界三大数学难题之一,是在1742年,由德国中学教师哥德
巴赫在教学中首先发现的. 1742年6月7日,哥德巴赫写信给当时的大数学家欧拉,
正式提出了以下的猜想:
(1)任何一个大于 6的偶数都可以表示成两个质数之和;
(2)任何一个大于9的奇数都可以表示成三个质数之和.
这就是哥德巴赫猜想.
欧拉在回信中说,他相信这个猜想是正确的,但他不能证明.从此,这道数学难题引
起了几乎所有数学家的注意.哥德巴赫猜想由此成为数学皇冠上一颗可望而不可
即的“明珠”.
中国数学家陈景润于1966年证明:“任何充分大的偶数都是一个质数与两个质数
的乘积的和”,通常这个结果表示为 “1+2”,即陈氏定理,这是目前这个问题的
最佳结果.
科学猜想也是命题.哥德巴赫猜想是一个迄今为止仍然没有得到正面证明也没有
被推翻的命题.
问题
1.哥德巴赫猜想是全称量词命题吗
提示:含有全称量词“任何”.
2.你能写出哥德巴赫猜想的否定形式吗
提示:全称量词命题的否定是存在量词命题.
1.判断一个命题是全称量词命题还是存在量词命题,关键是看命题中含有的量词
是全称量词还是存在量词.需要注意的是有些全称量词命题的全称量词可以省略
不写.
2.要判定全称量词命题“ x∈M,p(x)”是真命题,需要对集合M中的每个元素x,
验证p(x)成立.但要判定该命题是假命题,只需举出集合M中的一个x=x0,使p(x0)不
成立即可.要判定存在量词命题“ x∈M,p(x)”是真命题,只需在集合M中能找
到一个x=x0,使p(x0)成立即可;否则,这一命题就是假命题.
3.全称(存在)量词命题的否定是将其全称量词(存在量词)改为存在量词(全称量
词),并把结论否定,即“改量词,否结论”.
4.命题与命题的否定的真假相反.当命题的否定的真假不易判断时,可以通过判断
原命题的真假来得出命题的否定的真假.
(2020湖南常德第二中学高一上阶段测试)判断下列命题是全称量词命题还是存
在量词命题,并判断其真假.
(1)至少有一个整数,它既能被11整除,又能被9整除;
(2)对任意非零实数x1,x2,若x1 ;
(3)对任意的x∈R,x2+x+1=0都成立;
(4) x∈R,使得x2+1=0.
解析 (1)存在量词命题.因为99既能被11整除,又能被9整除,所以该命题是真
命题.
(2)全称量词命题.存在x1=-1,x2=1,x1(3)全称量词命题.因为存在x=0使x2+x+1=0不成立,所以该命题是假命题.
(4)存在量词命题.因为对任意x∈R,x2+1>0,所以该命题是假命题.
导师点睛 判断全称量词命题、存在量词命题的真假时,一般从反例、特例入
手,若找不到反例、特例,则再进行相关证明并得出结论:若 x∈M,p(x)成立,则全
称量词命题为真;若 x∈M,p(x)不成立,则存在量词命题为假.
写出下列命题的否定,并判断其真假.
(1)对任意x∈R,x2-x+ ≥0;
(2)所有的正方形都是矩形;
(3)至少有一个实数x,使x3+1=0.
思路点拨
变换量词,否定结论.
解析 (1)存在x∈R,x2-x+ <0,是假命题.
(2)至少存在一个正方形不是矩形,是假命题.
(3)对任意x∈R,x3+1≠0,是假命题.
2|全称量词命题和存在量词命题及其否定中的求参问题
解决含有量词的命题求参问题的思路
(1)全称量词命题求参的问题,常以一次函数、二次函数等为载体进行考查,一般
为“恒成立”问题.解决此类问题时,可构造函数,利用数形结合求参数的取值范
围,也可用分离参数法求参数的取值范围.
(2)存在量词命题求参数范围的问题中常出现“存在”等词语,对于此类问题,通
常是假设存在满足条件的参数,然后利用条件求参数范围,若能求出参数范围,则
假设成立;否则,假设不成立.解决有关存在量词命题的参数的取值范围问题时,一
般转化为“有解”问题,求解时应尽量分离参数.
常见结论:
1. x∈R,y=0,等价于方程y=0有实数根;
2. x∈R,y>0,就是不等式y>0恒成立,等价于ymin>0;
3. x∈R,y>0,就是不等式y>0有解,等价于ymax>0;
4. x∈R,y<0,就是不等式y<0恒成立,等价于ymax<0;
5. x∈R,y<0,就是不等式y<0有解,等价于ymin<0.
对于命题p的有些问题,正面解决很难或者很复杂,这时我们可以考虑它的反面,即
把命题p的问题转化成命题 p的问题,从而把问题简化,即“正难则反”的方法,也
就是“补集思想”的应用.
对于命题的否定,要注意一些常见否定词语的使用,下面是常用的正面叙述词语
和它的否定词语.
原词语 等于(=) 小于(<) 有 是 都是
否定词语 不等于(≠) 不小于(≥) 没有 不是 不都是
原词语 至少有一个 至多有一个 至多有n个
否定词语 一个也没有 至少有两个 至少有
(n+1)个
已知命题p: x∈R,x2+2x+a≥0,若命题q: x∈ ,x2-a≤0.若命题p
和命题q至多有一个为真命题,求实数a的取值范围.
思路点拨
本题若从正面解题需分类讨论,情况较多,所以可从结论的反面入手,即考虑p、q
均为真命题的情况,然后求其补集,即“补集思想”的应用.
解析 若命题p: x∈R,x2+2x+a≥0为真命题,
则Δ=22-4a≤0,
∴a≥1.
若命题q: x∈ ,x2-a≤0为真命题,
则a≥(x2)min,
∴a≥0.
∴p,q均为真命题时,满足
即{a|a≥1},
其补集为{a|a<1},
∴p,q至多有一个为真命题时,实数a的取值范围为{a|a<1}.
13.已知命题p: x∈{x|00},mx2+4x-1≠0.若p是真命题,q是假命题,求实数m的取值范围.
答案
解析 ∵ x∈R,x2+x+a≥0,∴Δ=12-4a≤0,∴a≥,∴a的取值范围为.
1.5 全称量词与存在量词
1 | 全称量词与全称量词命题
全称量词 全称量词命题 全称量词命题
的真假判断
短语“所有的”“任意一个”在逻辑中通常叫做① 全称量词 ,并用符号“② ”表示 含有全称量词的命题,叫做全称量词命题.全称量词命题“对M中任意一个x,p(x)成立”可用符号简记为③ x∈M,p(x) 全真为真,
一假为假
2 | 存在量词与存在量词命题
存在量词 存在量词命题 存在量词命题
的真假判断
短语“存在一个”“至少有一个”在逻辑中通常叫做④ 存在量词 ,并用符号“⑤ ”表示 含有存在量词的命题,叫做存在量词命题.存在量词命题“存在M中的元素x,p(x)成立”可用符号简记为⑥ x∈M,p(x) 一真为真,
全假为假
1.将一个命题的结论换成原来结论的反面,条件不变,得到一个新的命题,这个命
题就是原来命题的否定.如原来的命题为p:若s,则t,则它的否定为 p:⑦ 若s,则 t .
2.一个命题与它的否定不能同时为真,也不能同时为假,只能是⑧ 一真一假 .
3 | 命题的否定
4 | 全称量词命题和存在量词命题的否定
命题的类型 命题的符号表示 命题的否定的符号表示 命题的否定的类型
全称量词命题 p: x∈M,p(x) p:⑨ x∈M, p(x) 存在量词命题
存在量词命题 p: x∈M,p(x) p:⑩ x∈M, p(x) 全称量词命题
1.“有些”“有一个”“有的”是存在量词. ( √ )
2.全称量词命题“自然数都是正整数”是真命题. ( )
提示:0是自然数,但0不是正整数,因此“自然数都是正整数”是假命题.
3.在全称量词命题和存在量词命题中,量词都可以省略. ( )
提示:在存在量词命题中,量词不能省略,有些全称量词命题的量词可以省略.
4.命题p:“ x∈M,p(x)”的否定是“ x∈M, p(x)”,它们可以同真同假. ( )
5.若命题 p是存在量词命题,则命题p是全称量词命题.( √ )
6.用自然语言描述的全称量词命题的否定形式是唯一的.( )
提示:用自然语言描述的全称量词命题的否定形式并不唯一,如“所有的菱形都
是平行四边形”,它的否定可以是“并不是所有的菱形都是平行四边形”,也可
以是“有些菱形不是平行四边形”.
判断正误,正确的画“ √” ,错误的画“ ” .
1 | 全称量词命题、存在量词命题及其否定的真假判断
哥德巴赫猜想是世界三大数学难题之一,是在1742年,由德国中学教师哥德
巴赫在教学中首先发现的. 1742年6月7日,哥德巴赫写信给当时的大数学家欧拉,
正式提出了以下的猜想:
(1)任何一个大于 6的偶数都可以表示成两个质数之和;
(2)任何一个大于9的奇数都可以表示成三个质数之和.
这就是哥德巴赫猜想.
欧拉在回信中说,他相信这个猜想是正确的,但他不能证明.从此,这道数学难题引
起了几乎所有数学家的注意.哥德巴赫猜想由此成为数学皇冠上一颗可望而不可
即的“明珠”.
中国数学家陈景润于1966年证明:“任何充分大的偶数都是一个质数与两个质数
的乘积的和”,通常这个结果表示为 “1+2”,即陈氏定理,这是目前这个问题的
最佳结果.
科学猜想也是命题.哥德巴赫猜想是一个迄今为止仍然没有得到正面证明也没有
被推翻的命题.
问题
1.哥德巴赫猜想是全称量词命题吗
提示:含有全称量词“任何”.
2.你能写出哥德巴赫猜想的否定形式吗
提示:全称量词命题的否定是存在量词命题.
1.判断一个命题是全称量词命题还是存在量词命题,关键是看命题中含有的量词
是全称量词还是存在量词.需要注意的是有些全称量词命题的全称量词可以省略
不写.
2.要判定全称量词命题“ x∈M,p(x)”是真命题,需要对集合M中的每个元素x,
验证p(x)成立.但要判定该命题是假命题,只需举出集合M中的一个x=x0,使p(x0)不
成立即可.要判定存在量词命题“ x∈M,p(x)”是真命题,只需在集合M中能找
到一个x=x0,使p(x0)成立即可;否则,这一命题就是假命题.
3.全称(存在)量词命题的否定是将其全称量词(存在量词)改为存在量词(全称量
词),并把结论否定,即“改量词,否结论”.
4.命题与命题的否定的真假相反.当命题的否定的真假不易判断时,可以通过判断
原命题的真假来得出命题的否定的真假.
(2020湖南常德第二中学高一上阶段测试)判断下列命题是全称量词命题还是存
在量词命题,并判断其真假.
(1)至少有一个整数,它既能被11整除,又能被9整除;
(2)对任意非零实数x1,x2,若x1
(3)对任意的x∈R,x2+x+1=0都成立;
(4) x∈R,使得x2+1=0.
解析 (1)存在量词命题.因为99既能被11整除,又能被9整除,所以该命题是真
命题.
(2)全称量词命题.存在x1=-1,x2=1,x1
(4)存在量词命题.因为对任意x∈R,x2+1>0,所以该命题是假命题.
导师点睛 判断全称量词命题、存在量词命题的真假时,一般从反例、特例入
手,若找不到反例、特例,则再进行相关证明并得出结论:若 x∈M,p(x)成立,则全
称量词命题为真;若 x∈M,p(x)不成立,则存在量词命题为假.
写出下列命题的否定,并判断其真假.
(1)对任意x∈R,x2-x+ ≥0;
(2)所有的正方形都是矩形;
(3)至少有一个实数x,使x3+1=0.
思路点拨
变换量词,否定结论.
解析 (1)存在x∈R,x2-x+ <0,是假命题.
(2)至少存在一个正方形不是矩形,是假命题.
(3)对任意x∈R,x3+1≠0,是假命题.
2|全称量词命题和存在量词命题及其否定中的求参问题
解决含有量词的命题求参问题的思路
(1)全称量词命题求参的问题,常以一次函数、二次函数等为载体进行考查,一般
为“恒成立”问题.解决此类问题时,可构造函数,利用数形结合求参数的取值范
围,也可用分离参数法求参数的取值范围.
(2)存在量词命题求参数范围的问题中常出现“存在”等词语,对于此类问题,通
常是假设存在满足条件的参数,然后利用条件求参数范围,若能求出参数范围,则
假设成立;否则,假设不成立.解决有关存在量词命题的参数的取值范围问题时,一
般转化为“有解”问题,求解时应尽量分离参数.
常见结论:
1. x∈R,y=0,等价于方程y=0有实数根;
2. x∈R,y>0,就是不等式y>0恒成立,等价于ymin>0;
3. x∈R,y>0,就是不等式y>0有解,等价于ymax>0;
4. x∈R,y<0,就是不等式y<0恒成立,等价于ymax<0;
5. x∈R,y<0,就是不等式y<0有解,等价于ymin<0.
对于命题p的有些问题,正面解决很难或者很复杂,这时我们可以考虑它的反面,即
把命题p的问题转化成命题 p的问题,从而把问题简化,即“正难则反”的方法,也
就是“补集思想”的应用.
对于命题的否定,要注意一些常见否定词语的使用,下面是常用的正面叙述词语
和它的否定词语.
原词语 等于(=) 小于(<) 有 是 都是
否定词语 不等于(≠) 不小于(≥) 没有 不是 不都是
原词语 至少有一个 至多有一个 至多有n个
否定词语 一个也没有 至少有两个 至少有
(n+1)个
已知命题p: x∈R,x2+2x+a≥0,若命题q: x∈ ,x2-a≤0.若命题p
和命题q至多有一个为真命题,求实数a的取值范围.
思路点拨
本题若从正面解题需分类讨论,情况较多,所以可从结论的反面入手,即考虑p、q
均为真命题的情况,然后求其补集,即“补集思想”的应用.
解析 若命题p: x∈R,x2+2x+a≥0为真命题,
则Δ=22-4a≤0,
∴a≥1.
若命题q: x∈ ,x2-a≤0为真命题,
则a≥(x2)min,
∴a≥0.
∴p,q均为真命题时,满足
即{a|a≥1},
其补集为{a|a<1},
∴p,q至多有一个为真命题时,实数a的取值范围为{a|a<1}.
13.已知命题p: x∈{x|0
答案
解析 ∵ x∈R,x2+x+a≥0,∴Δ=12-4a≤0,∴a≥,∴a的取值范围为.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
