1.2集合间的基本关系 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共30张PPT)
文档属性
| 名称 | 1.2集合间的基本关系 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 21:08:20 | ||
图片预览








文档简介
(共30张PPT)
1.2 集合间的基本关系
1 | 子集、集合相等、真子集
概念 图示 性质
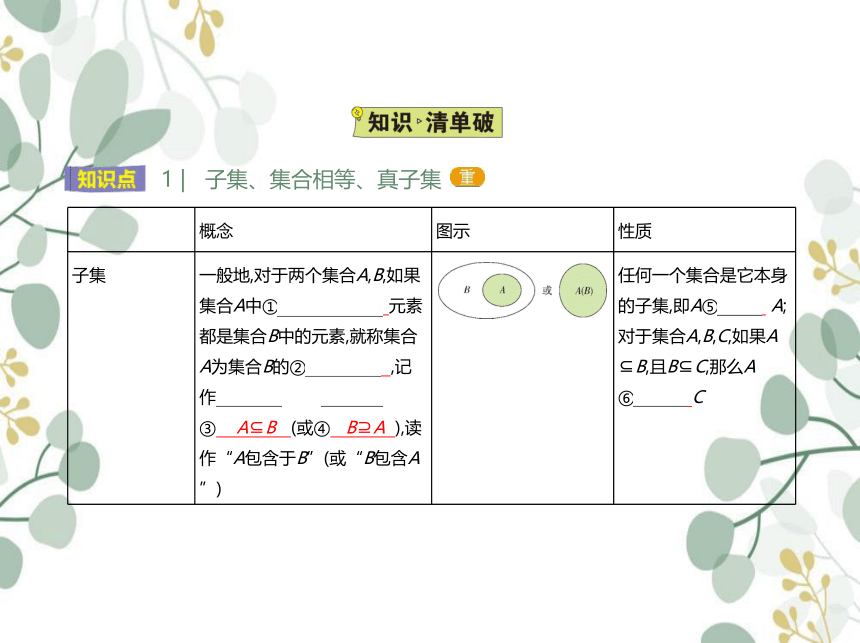
子集 一般地,对于两个集合A,B,如果集合A中① 任意一个 元素都是集合B中的元素,就称集合A为集合B的② 子集 ,记作 ③ A B (或④ B A ),读作“A包含于B”(或“B包含A”) 任何一个集合是它本身的子集,即A⑤ A;
对于集合A,B,C,如果A B,且B C,那么A
⑥ C
概念 图示 性质
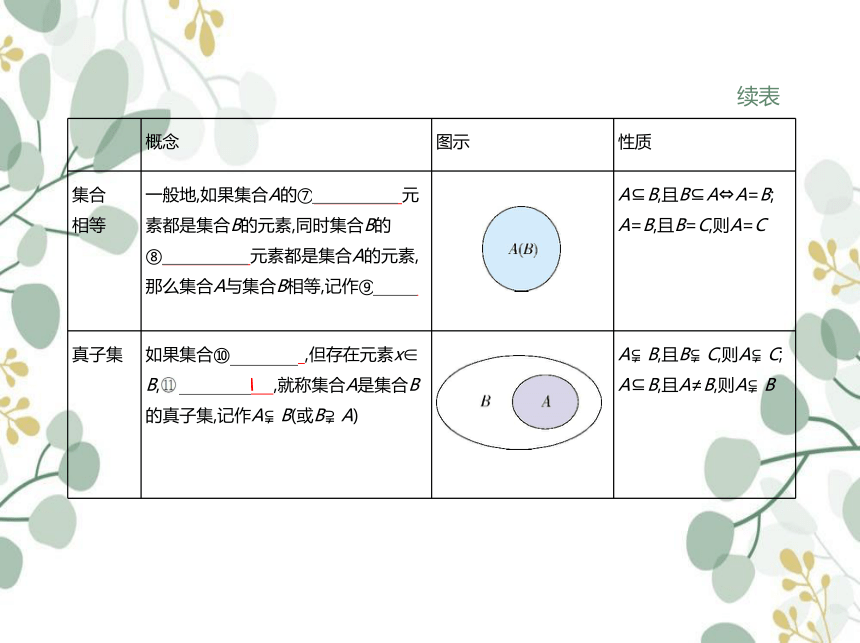
集合 相等 一般地,如果集合A的⑦ 任何一 元素都是集合B的元素,同时集合B的 ⑧任何一个 元素都是集合A的元素,那么集合A与集合B相等,记作⑨ AB A B,且B A A=B;
A=B,且B=C,则A=C
真子集 如果集合⑩ A B ,但存在元素x∈B,且 x A ,就称集合A是集合B的真子集,记作A B(或B A) A B,且B C,则A C;
A B,且A≠B,则A B
续表
2 | 空集
定义 不含任何元素 的集合叫做空集
符号
规定 空集是任何集合的子集,是任何非空集合的真子集
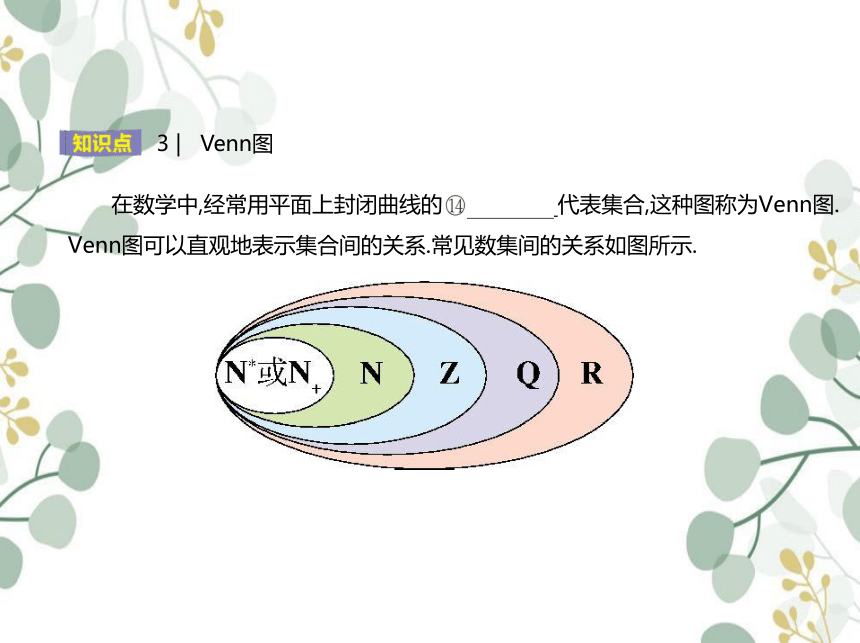
在数学中,经常用平面上封闭曲线的 内部 代表集合,这种图称为Venn图.
Venn图可以直观地表示集合间的关系.常见数集间的关系如图所示.
3 | Venn图
0,{0}, ,{ }之间的关系
(1) 不含任何元素,所以0不是它的元素.
(2){0}表示只含有一个元素0的集合,所以0∈{0}.
(3){ }并不是空集,{ }中有一个元素,这个元素就是 ,即 ∈{ }.又因为 是
任何集合的子集,是任何非空集合的真子集,所以 { }.
判断下列集合的关系:
(1)A={1,2,3},B={x |(x-1)(x-2)(x-3)=0};
(2)A={x |0<2x-1<1},B={x |1<3x+1<4};
(3)A={x |x是文学作品},B={x|x是散文},C={x|x是叙事散文};
(4)M=x x=m+ ,m ∈Z,N= x x= - ,n∈Z ,P=x x= + ,k∈Z .
思路点拨
(1)先确定集合B中的元素,再与集合A中的元素对比.
(2)先确定集合A,B,再用数轴表示,即可得结果.
(3)利用Venn图表示集合A,B,C间的关系,即可得结果.
(4)先分析集合M,N,P的元素特征(也可用列举法),再判断集合M,N,P的关系.
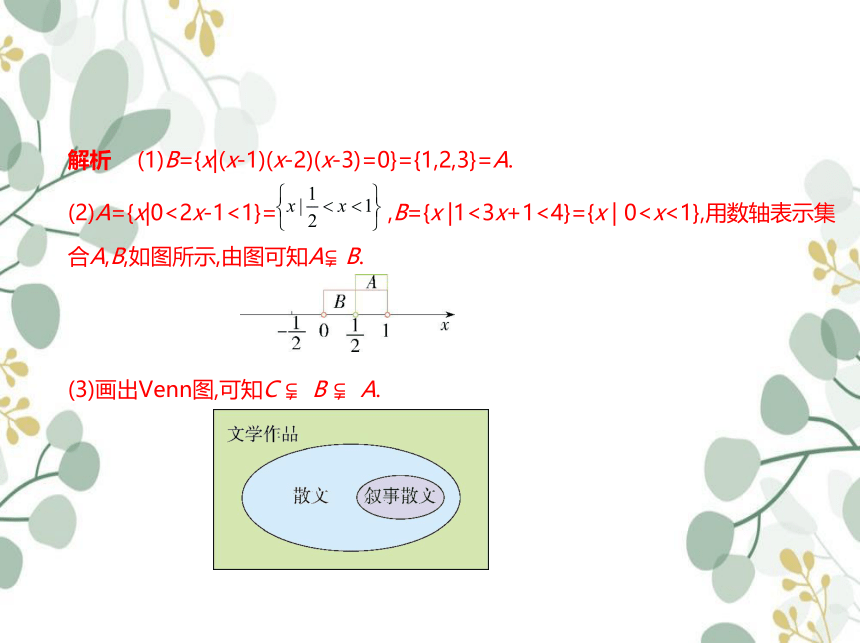
解析 (1)B={x|(x-1)(x-2)(x-3)=0}={1,2,3}=A.
(2)A={x|0<2x-1<1}= ,B={x |1<3x+1<4}={x | 0合A,B,如图所示,由图可知A B.
(3)画出Venn图,可知C B A.
(4)解法一:元素特征法.
M= =
= ,
N= =
= ,
P= = ,
∴M N=P.
2 | 已知集合间的关系求参数
已知集合A={3,1},B={m,1},若集合A,B相等,则可由集合间的关系得到集合的
元素之间的关系,进而可以求出参数m的值为3.
问题
1.已知集合A={2,-1},B={m2-m,-1},若A=B,如何求实数m的值
提示:由A=B得m2-m=2,即m2-m-2=0,解得m=2或m=-1.
2.已知集合A={x|1≤x≤2},集合B={x|1≤x≤a,a≥1},若A B,如何求a的取值范围
提示:若A B,画出数轴:
则由数轴可知a>2.
3.在问题2中,将条件改为“B A”,又如何求a的取值范围
提示:若B A,画出数轴:
则由数轴可知1≤a≤2.
根据集合间的关系,求参数的值或取值范围的方法
1.若集合是用列举法表示的,则根据集合间的关系,转化为方程(组)求解,同时注意
考虑元素的互异性;若集合是用不等式描述的,则利用数轴转化为不等式(组)求
解,同时还要注意验证端点值的取舍.
2.涉及“A B”或“A B”的问题,若集合A中含有参数,通常要分A= 和A≠
两种情况进行讨论,其中A= 的情况容易被忽略,应引起足够的重视.
求满足下列条件的实数a的值或取值范围:
(1)已知集合M={a-3,2a-1,a2+1},N={-2,4a-3,3a-1},M=N;
(2)已知集合M={x|ax+2=0},N={x|x2-5x+6=0},M N;
(3)已知集合M={x|-3(4)(2020山东济宁高一上期中)已知集合M={x|x2-3x+2=0},N={x|x2+2(a+1)x+(a2-5)=
0},N M.
思路点拨
分别根据集合间的关系列出关系式,求出a的值或取值范围.
3 | 探究已知集合的子集个数
如果一个集合有n (n∈N*)个元素,那么如何研究它的子集个数
问题
1.已知集合A={a,b,c},集合A有几个子集
提示:集合A有8个子集.
2.已知集合A={a,b,c},如何写出集合A的所有子集
提示:对于有限集的子集,通常按子集中元素个数的多少及集合中元素的先后顺
序来写.
3.已知集合A={a,b,c},集合A的真子集有几个 非空真子集有几个
提示:集合A的真子集有23-1=7个,非空真子集有23-2=6个.
1.假设集合A中含有n(n∈N*)个元素,则:
(1)A的子集个数是2n;
(2)A的非空子集个数是2n-1;
(3)A的真子集个数是2n-1;
(4)A的非空真子集个数是2n-2.
2.设有限集合A,B中分别含有m个,n个元素(m,n∈N*,m≤n),且A C B,则符合条
件的有限集C的个数为2n-m.
3.求给定集合的子集的两个注意点:
(1)按子集中元素个数的多少,以一定的顺序来写;
(2)在写子集时要注意空集和集合本身也是该集合的子集.
已知集合A={2,4,6,8,9},B={1,2,3,5,8},存在非空集合C,使C中每个元素都加上
2就变成了A的一个子集,且C中的每个元素都减去2就变成了B的一个子集,则集
合C 的个数是多少
解析 假设存在满足条件的集合C,则C≠ ,将A中元素都减2得{0,2,4,6,7},B中元
素都加2得{3,4,5,7,10},于是C {0,2,4,6,7},且C {3,4,5,7,10}.注意到两个集合的
共同元素构成的集合为{4,7},故非空集合C是{4,7}的子集,即C={4,7}或C={4}或
C={7},故集合C的个数为3.
题组一 子集、真子集和空集
1.(2021重庆巴蜀中学高一上月考)已知集合A={0,1},则集合A的子集个数是 ( )
A.1 B.2 C.3 D.4
2.下列四个集合中,是空集的是 ( )
A.{x|x+3=3}
B.{(x,y)|y2=-x2,x,y∈R}
C.{x|x2≤0}
D.{x|x2-x+1=0,x∈R}
3.(2020广东实验中学高二开学摸底考试)下列六个关系式:①{a,b} {b,a};②{a,b}={b,a};③0= ;④0∈{0};⑤ ∈{0};⑥ {0},其中正确的个
数为 ( )
A.6 B.5 C.4 D.3
4.若集合S={x|x=3n+1,n∈N},T={x|x=3k-2,k∈Z},则 ( )
A.S T B.T S C.S =T D.S T
5.(2020四川乐山高一上期末)已知集合U=R,则正确表示集合M={-1,0,1}和N={x|x2-x=0}关系的Venn图是 ( )
6.(多选)下列说法中,正确的是 ( )
A.空集是任何集合的真子集
B.若A B,B C,则A C
C.任何一个集合必有两个或两个以上的真子集
D.若不属于B的元素一定不属于A,则A B
7.(2020河南郑州高一上期末)已知集合M满足{3,4} M {3,4,5,6},则满足条件的集合M有
个.
题组二 集合相等及其应用
8.已知集合A=,B=,C=,则下列结论正确的是( )
A.A=B B.A=C C.B=C D.A=B=C
9.(2020贵州兴仁凤凰中学高一月考)若{5,a+4}={a,b},则a+b= .
10.已知集合A=,B=xx=k±,k∈Z,则集合A,B之间的关系为 .
题组三 由集合间的关系解决参数问题
11.(2020四川绵阳中学高一上月考)已知集合A={1,3,},B={1,m},B A,则m=( )
A.0或3 B.0或1
C.1 D.3
12.已知 {x|x2-x+a=0},则实数a的取值范围是( )
A.a< B.a≤ C.a≥ D.a>
13.(2021安徽安庆高一上检测)已知集合A={x|x>3或x<1},B={x|x-a<0},若B A,则实数a的取值范围是( )
A.a>3 B.a≥3 C.a<1 D.a≤1
14.(2020山西忻州第一中学高一上期中)已知M={2,a,b},N={2a,2,b2},若M=N,求a与b的值.
15.(2020河北石家庄第二中学高一上期中)设集合A={x|x2-8x+15=0},B={x|ax-1=0}.
(1)若a=,试判断集合A与B之间的关系;
(2)若B A,求实数a的取值集合.
题组一 子集、真子集和空集
1.()设集合A={1,0},集合B={2,3},集合M={x|x=b(a+b),a∈A,b∈B},则集合M的真子集的个数为 ( )
A.7 B.12 C.16 D.15
2.(2020上海华东师范大学第二附属中学高三下月考,)已知非空集合M满足:对任意x∈M,总有x2 M,且 M,若M {0,1,2,3,4,5},则满足条件的M的个数是 ( )
A.11 B.12 C.15 D.16
3.(2020北京第八中学高一上月考,)已知 集合M=,N=,P=,则M,N,P的关系为( )
A.M=N P B.M N=P
C.M N P D.N P M
题组二 由集合间的关系解决参数问题
6.(2021山西运城高一上检测,)集合M={1,2,a,a2-3a-1},N={-1,3},若3∈M且N M,则a的取值为
( )
A.-1 B.4 C.-1或4 D.3
7.(2021广东揭阳高一上检测,)若集合A={x|ax2-2ax+a-1=0}= ,则实数a的取值范围是 .
8.(2020山东泰安英雄山中学高一月考,)设集合A={x|-1≤x+1≤6},B={x|m-19.(2021四川成都第七中学高三上月考,)已知集合{a,b,c}={0,1,2},有下列三个关 系:①a≠2;②b=2;③c≠0,若这三个关系中有且只有一个是正确的,则a+2b+3c= .
11.(2020甘肃名校高一上期中联考,)已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1或x>16}.
(1)若A为非空集合,求实数a的取值范围;
(2)若A B,求实数a的取值范围.
12.(2020湖南长沙一中高一月考,)已知集合A={x|ax2-3x+2=0}.
(1)若 A,求实数a的取值范围;
(2)若B={x|x2-x=0},且A B,求实数a的取值范围.
考点1 集合的基本运算
1.(2020北京,1,4分,)已知集合A={-1,0,1,2},B={x|0A.{-1,0,1} B.{0,1} C.{-1,1,2} D.{1,2}
2.(2020全国Ⅱ理,1,5分,)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则 U(A∪B)
= ( )
A.{-2,3} B.{-2,2,3}
C.{-2,-1,0,3} D.{-2,-1,0,2,3}
3.(2020天津,1,5分,)设全集U={-3,-2,-1,0,1,2,3},集合A={-1,0,1,2},B={-3,0,2,3},则A∩( UB)=( )
A.{-3,3} B.{0,2}
C.{-1,1} D.{-3,-2,-1,1,3}
4.(2020全国新高考Ⅰ,1,5分,)设集合A={x|1≤x≤3},B={x|2A.{x|2C.{x|1≤x<4} D.{x|1考点2 集合基本运算的应用
5.(2020全国Ⅲ文,1,5分,)已知集合A={1,2,3,5,7,11},B={x|3A.2 B.3 C.4 D.5
6.(2020全国Ⅲ理,1,5分,)已知集合A={(x,y)|x,y∈N*,y≥x},B={(x,y)|x+y=8},则A∩B中元素的个数为 ( )
A.2 B.3 C.4 D.6
7.(2020浙江,10,4分,)设集合S,T,S N*,T N*,S,T中至少有2个元素,且S,T满足:①对于任意的x,y∈S,若x≠y,则xy∈T;②对于任意的x,y∈T,若xA.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
应用实践
1.(2021江西新余第六中学高一期中,)设全集I是实数集R,M={x|x≥3},N={x|2≤x≤5}都是I的子集(如图所示),则阴影部分所表示的集合为 ( )
A.{x|2C.{x|22.(2021湖湘名校教育联盟高一月考,)设全集U=A∪B={x|-1≤x<3},A∩( UB)={x|2A.{x|-1≤x<2} B.{x|-1≤x≤2}
C.{x|23.(2020湖南长沙长郡中学高一上月考,)已知集合A={x|x<-3或x>1},B={x|x≤-4或x>a},若A∩( RB)中恰好含有2个整数,则实数a的取值范围是 ( )
A.3C.3迁移应用
5.(2020北京昌平高一上月考,)对于正整数集合A={a1,a2,…,an}(n∈N*,n≥3),若去掉其中任意一个元素ai(i=1,2,…,n)之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,则称集合A为“和谐集”.
(1)判断集合{1,2,3,4,5}是不是“和谐集”(不必写过程);
(2)请写出一个只含有7个元素的“和谐集”,并证明此集合为“和谐集”;
(3)当n=5时,集合A={a1,a2,a3,a4,a5},求证:集合A不是“和谐集”.
.解析 (1)集合{1,2,3,4,5}不是“和谐集”.
(2)集合{1,3,5,7,9,11,13}为“和谐集”.
证明如下:
∵3+5+7+9=11+13,
1+9+13=5+7+11,
9+13=1+3+7+11,
1+9+11=3+5+13,
1+3+5+11=7+13,
3+7+9=1+5+13,
1+3+5+9=7+11,
∴集合{1,3,5,7,9,11,13}是“和谐集”.
(3)证明:假设集合A是“和谐集”.不妨设0则有a1+a5=a3+a4①,或a5=a1+a3+a4②,
集合{a2,a3,a4,a5}也能分成两个交集为空集的子集,且两个子集元素之和相等,
则有a2+a5=a3+a4③,或a5=a2+a3+a4④,
由①③,得a1=a2,
由①④,得a1=-a2,
由②③,得a1=-a2,
由②④,得a1=a2,
都与假设矛盾,所以假设不成立.
故当n=5时,集合A一定不是“和谐集”.
名师点睛 解决新定义下的集合问题时,首先要将新定义理解清楚,然后根据定义验证、证明即可,同时注意思考问题的全面性.
1.2 集合间的基本关系
1 | 子集、集合相等、真子集
概念 图示 性质
子集 一般地,对于两个集合A,B,如果集合A中① 任意一个 元素都是集合B中的元素,就称集合A为集合B的② 子集 ,记作 ③ A B (或④ B A ),读作“A包含于B”(或“B包含A”) 任何一个集合是它本身的子集,即A⑤ A;
对于集合A,B,C,如果A B,且B C,那么A
⑥ C
概念 图示 性质
集合 相等 一般地,如果集合A的⑦ 任何一 元素都是集合B的元素,同时集合B的 ⑧任何一个 元素都是集合A的元素,那么集合A与集合B相等,记作⑨ AB A B,且B A A=B;
A=B,且B=C,则A=C
真子集 如果集合⑩ A B ,但存在元素x∈B,且 x A ,就称集合A是集合B的真子集,记作A B(或B A) A B,且B C,则A C;
A B,且A≠B,则A B
续表
2 | 空集
定义 不含任何元素 的集合叫做空集
符号
规定 空集是任何集合的子集,是任何非空集合的真子集
在数学中,经常用平面上封闭曲线的 内部 代表集合,这种图称为Venn图.
Venn图可以直观地表示集合间的关系.常见数集间的关系如图所示.
3 | Venn图
0,{0}, ,{ }之间的关系
(1) 不含任何元素,所以0不是它的元素.
(2){0}表示只含有一个元素0的集合,所以0∈{0}.
(3){ }并不是空集,{ }中有一个元素,这个元素就是 ,即 ∈{ }.又因为 是
任何集合的子集,是任何非空集合的真子集,所以 { }.
判断下列集合的关系:
(1)A={1,2,3},B={x |(x-1)(x-2)(x-3)=0};
(2)A={x |0<2x-1<1},B={x |1<3x+1<4};
(3)A={x |x是文学作品},B={x|x是散文},C={x|x是叙事散文};
(4)M=x x=m+ ,m ∈Z,N= x x= - ,n∈Z ,P=x x= + ,k∈Z .
思路点拨
(1)先确定集合B中的元素,再与集合A中的元素对比.
(2)先确定集合A,B,再用数轴表示,即可得结果.
(3)利用Venn图表示集合A,B,C间的关系,即可得结果.
(4)先分析集合M,N,P的元素特征(也可用列举法),再判断集合M,N,P的关系.
解析 (1)B={x|(x-1)(x-2)(x-3)=0}={1,2,3}=A.
(2)A={x|0<2x-1<1}= ,B={x |1<3x+1<4}={x | 0
(3)画出Venn图,可知C B A.
(4)解法一:元素特征法.
M= =
= ,
N= =
= ,
P= = ,
∴M N=P.
2 | 已知集合间的关系求参数
已知集合A={3,1},B={m,1},若集合A,B相等,则可由集合间的关系得到集合的
元素之间的关系,进而可以求出参数m的值为3.
问题
1.已知集合A={2,-1},B={m2-m,-1},若A=B,如何求实数m的值
提示:由A=B得m2-m=2,即m2-m-2=0,解得m=2或m=-1.
2.已知集合A={x|1≤x≤2},集合B={x|1≤x≤a,a≥1},若A B,如何求a的取值范围
提示:若A B,画出数轴:
则由数轴可知a>2.
3.在问题2中,将条件改为“B A”,又如何求a的取值范围
提示:若B A,画出数轴:
则由数轴可知1≤a≤2.
根据集合间的关系,求参数的值或取值范围的方法
1.若集合是用列举法表示的,则根据集合间的关系,转化为方程(组)求解,同时注意
考虑元素的互异性;若集合是用不等式描述的,则利用数轴转化为不等式(组)求
解,同时还要注意验证端点值的取舍.
2.涉及“A B”或“A B”的问题,若集合A中含有参数,通常要分A= 和A≠
两种情况进行讨论,其中A= 的情况容易被忽略,应引起足够的重视.
求满足下列条件的实数a的值或取值范围:
(1)已知集合M={a-3,2a-1,a2+1},N={-2,4a-3,3a-1},M=N;
(2)已知集合M={x|ax+2=0},N={x|x2-5x+6=0},M N;
(3)已知集合M={x|-3
0},N M.
思路点拨
分别根据集合间的关系列出关系式,求出a的值或取值范围.
3 | 探究已知集合的子集个数
如果一个集合有n (n∈N*)个元素,那么如何研究它的子集个数
问题
1.已知集合A={a,b,c},集合A有几个子集
提示:集合A有8个子集.
2.已知集合A={a,b,c},如何写出集合A的所有子集
提示:对于有限集的子集,通常按子集中元素个数的多少及集合中元素的先后顺
序来写.
3.已知集合A={a,b,c},集合A的真子集有几个 非空真子集有几个
提示:集合A的真子集有23-1=7个,非空真子集有23-2=6个.
1.假设集合A中含有n(n∈N*)个元素,则:
(1)A的子集个数是2n;
(2)A的非空子集个数是2n-1;
(3)A的真子集个数是2n-1;
(4)A的非空真子集个数是2n-2.
2.设有限集合A,B中分别含有m个,n个元素(m,n∈N*,m≤n),且A C B,则符合条
件的有限集C的个数为2n-m.
3.求给定集合的子集的两个注意点:
(1)按子集中元素个数的多少,以一定的顺序来写;
(2)在写子集时要注意空集和集合本身也是该集合的子集.
已知集合A={2,4,6,8,9},B={1,2,3,5,8},存在非空集合C,使C中每个元素都加上
2就变成了A的一个子集,且C中的每个元素都减去2就变成了B的一个子集,则集
合C 的个数是多少
解析 假设存在满足条件的集合C,则C≠ ,将A中元素都减2得{0,2,4,6,7},B中元
素都加2得{3,4,5,7,10},于是C {0,2,4,6,7},且C {3,4,5,7,10}.注意到两个集合的
共同元素构成的集合为{4,7},故非空集合C是{4,7}的子集,即C={4,7}或C={4}或
C={7},故集合C的个数为3.
题组一 子集、真子集和空集
1.(2021重庆巴蜀中学高一上月考)已知集合A={0,1},则集合A的子集个数是 ( )
A.1 B.2 C.3 D.4
2.下列四个集合中,是空集的是 ( )
A.{x|x+3=3}
B.{(x,y)|y2=-x2,x,y∈R}
C.{x|x2≤0}
D.{x|x2-x+1=0,x∈R}
3.(2020广东实验中学高二开学摸底考试)下列六个关系式:①{a,b} {b,a};②{a,b}={b,a};③0= ;④0∈{0};⑤ ∈{0};⑥ {0},其中正确的个
数为 ( )
A.6 B.5 C.4 D.3
4.若集合S={x|x=3n+1,n∈N},T={x|x=3k-2,k∈Z},则 ( )
A.S T B.T S C.S =T D.S T
5.(2020四川乐山高一上期末)已知集合U=R,则正确表示集合M={-1,0,1}和N={x|x2-x=0}关系的Venn图是 ( )
6.(多选)下列说法中,正确的是 ( )
A.空集是任何集合的真子集
B.若A B,B C,则A C
C.任何一个集合必有两个或两个以上的真子集
D.若不属于B的元素一定不属于A,则A B
7.(2020河南郑州高一上期末)已知集合M满足{3,4} M {3,4,5,6},则满足条件的集合M有
个.
题组二 集合相等及其应用
8.已知集合A=,B=,C=,则下列结论正确的是( )
A.A=B B.A=C C.B=C D.A=B=C
9.(2020贵州兴仁凤凰中学高一月考)若{5,a+4}={a,b},则a+b= .
10.已知集合A=,B=xx=k±,k∈Z,则集合A,B之间的关系为 .
题组三 由集合间的关系解决参数问题
11.(2020四川绵阳中学高一上月考)已知集合A={1,3,},B={1,m},B A,则m=( )
A.0或3 B.0或1
C.1 D.3
12.已知 {x|x2-x+a=0},则实数a的取值范围是( )
A.a< B.a≤ C.a≥ D.a>
13.(2021安徽安庆高一上检测)已知集合A={x|x>3或x<1},B={x|x-a<0},若B A,则实数a的取值范围是( )
A.a>3 B.a≥3 C.a<1 D.a≤1
14.(2020山西忻州第一中学高一上期中)已知M={2,a,b},N={2a,2,b2},若M=N,求a与b的值.
15.(2020河北石家庄第二中学高一上期中)设集合A={x|x2-8x+15=0},B={x|ax-1=0}.
(1)若a=,试判断集合A与B之间的关系;
(2)若B A,求实数a的取值集合.
题组一 子集、真子集和空集
1.()设集合A={1,0},集合B={2,3},集合M={x|x=b(a+b),a∈A,b∈B},则集合M的真子集的个数为 ( )
A.7 B.12 C.16 D.15
2.(2020上海华东师范大学第二附属中学高三下月考,)已知非空集合M满足:对任意x∈M,总有x2 M,且 M,若M {0,1,2,3,4,5},则满足条件的M的个数是 ( )
A.11 B.12 C.15 D.16
3.(2020北京第八中学高一上月考,)已知 集合M=,N=,P=,则M,N,P的关系为( )
A.M=N P B.M N=P
C.M N P D.N P M
题组二 由集合间的关系解决参数问题
6.(2021山西运城高一上检测,)集合M={1,2,a,a2-3a-1},N={-1,3},若3∈M且N M,则a的取值为
( )
A.-1 B.4 C.-1或4 D.3
7.(2021广东揭阳高一上检测,)若集合A={x|ax2-2ax+a-1=0}= ,则实数a的取值范围是 .
8.(2020山东泰安英雄山中学高一月考,)设集合A={x|-1≤x+1≤6},B={x|m-1
11.(2020甘肃名校高一上期中联考,)已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1或x>16}.
(1)若A为非空集合,求实数a的取值范围;
(2)若A B,求实数a的取值范围.
12.(2020湖南长沙一中高一月考,)已知集合A={x|ax2-3x+2=0}.
(1)若 A,求实数a的取值范围;
(2)若B={x|x2-x=0},且A B,求实数a的取值范围.
考点1 集合的基本运算
1.(2020北京,1,4分,)已知集合A={-1,0,1,2},B={x|0
2.(2020全国Ⅱ理,1,5分,)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则 U(A∪B)
= ( )
A.{-2,3} B.{-2,2,3}
C.{-2,-1,0,3} D.{-2,-1,0,2,3}
3.(2020天津,1,5分,)设全集U={-3,-2,-1,0,1,2,3},集合A={-1,0,1,2},B={-3,0,2,3},则A∩( UB)=( )
A.{-3,3} B.{0,2}
C.{-1,1} D.{-3,-2,-1,1,3}
4.(2020全国新高考Ⅰ,1,5分,)设集合A={x|1≤x≤3},B={x|2
5.(2020全国Ⅲ文,1,5分,)已知集合A={1,2,3,5,7,11},B={x|3
6.(2020全国Ⅲ理,1,5分,)已知集合A={(x,y)|x,y∈N*,y≥x},B={(x,y)|x+y=8},则A∩B中元素的个数为 ( )
A.2 B.3 C.4 D.6
7.(2020浙江,10,4分,)设集合S,T,S N*,T N*,S,T中至少有2个元素,且S,T满足:①对于任意的x,y∈S,若x≠y,则xy∈T;②对于任意的x,y∈T,若x
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
应用实践
1.(2021江西新余第六中学高一期中,)设全集I是实数集R,M={x|x≥3},N={x|2≤x≤5}都是I的子集(如图所示),则阴影部分所表示的集合为 ( )
A.{x|2
C.{x|2
A.3
5.(2020北京昌平高一上月考,)对于正整数集合A={a1,a2,…,an}(n∈N*,n≥3),若去掉其中任意一个元素ai(i=1,2,…,n)之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,则称集合A为“和谐集”.
(1)判断集合{1,2,3,4,5}是不是“和谐集”(不必写过程);
(2)请写出一个只含有7个元素的“和谐集”,并证明此集合为“和谐集”;
(3)当n=5时,集合A={a1,a2,a3,a4,a5},求证:集合A不是“和谐集”.
.解析 (1)集合{1,2,3,4,5}不是“和谐集”.
(2)集合{1,3,5,7,9,11,13}为“和谐集”.
证明如下:
∵3+5+7+9=11+13,
1+9+13=5+7+11,
9+13=1+3+7+11,
1+9+11=3+5+13,
1+3+5+11=7+13,
3+7+9=1+5+13,
1+3+5+9=7+11,
∴集合{1,3,5,7,9,11,13}是“和谐集”.
(3)证明:假设集合A是“和谐集”.不妨设0
集合{a2,a3,a4,a5}也能分成两个交集为空集的子集,且两个子集元素之和相等,
则有a2+a5=a3+a4③,或a5=a2+a3+a4④,
由①③,得a1=a2,
由①④,得a1=-a2,
由②③,得a1=-a2,
由②④,得a1=a2,
都与假设矛盾,所以假设不成立.
故当n=5时,集合A一定不是“和谐集”.
名师点睛 解决新定义下的集合问题时,首先要将新定义理解清楚,然后根据定义验证、证明即可,同时注意思考问题的全面性.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
