2021-2022学年人教版 数学 七年级上册4.3.2 角的比较与运算作业 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版 数学 七年级上册4.3.2 角的比较与运算作业 (Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 16:50:36 | ||
图片预览


文档简介
4.3.2 角的比较与运算
一、计算题
1. 48 38′+72 32′ 2. 105 17 ′-58 58 ′
3.60 25 ′×8 4. 58 30 ′÷5
5.25 25′25″+65 65′65″ 6.175 -35 18′52 ″
7. 31 17′20 ″ ×5 8. 41 17′20 ″÷5
二、选择题
1.如图,在∠AOB内部任作一条射线OC,则下列结论一定成立的是( )
A.∠AOC>∠BOC B.∠BOC<∠AOB
C.∠AOC<∠BOC D.∠BOC>∠AOB
2.∠1和∠2的顶点和一边都重合,另一边都在公共边的同侧,且∠1>∠2,那么∠1的另一边落在∠2的 ( )
A.另一边上 B.内部
C.外部 D.内部或另一边上
3.已知∠AOB=80°,以O为端点作射线OC,使∠AOC=52°,则∠BOC的度数为 ( )
A.28° B.132° C.28°或132° D.68°
4.已知∠AOB=60°,∠AOC=∠AOB,射线OD平分∠BOC,则∠COD的度数为 ( )
A.15° B.45° C.15°或45° D.20°或40°
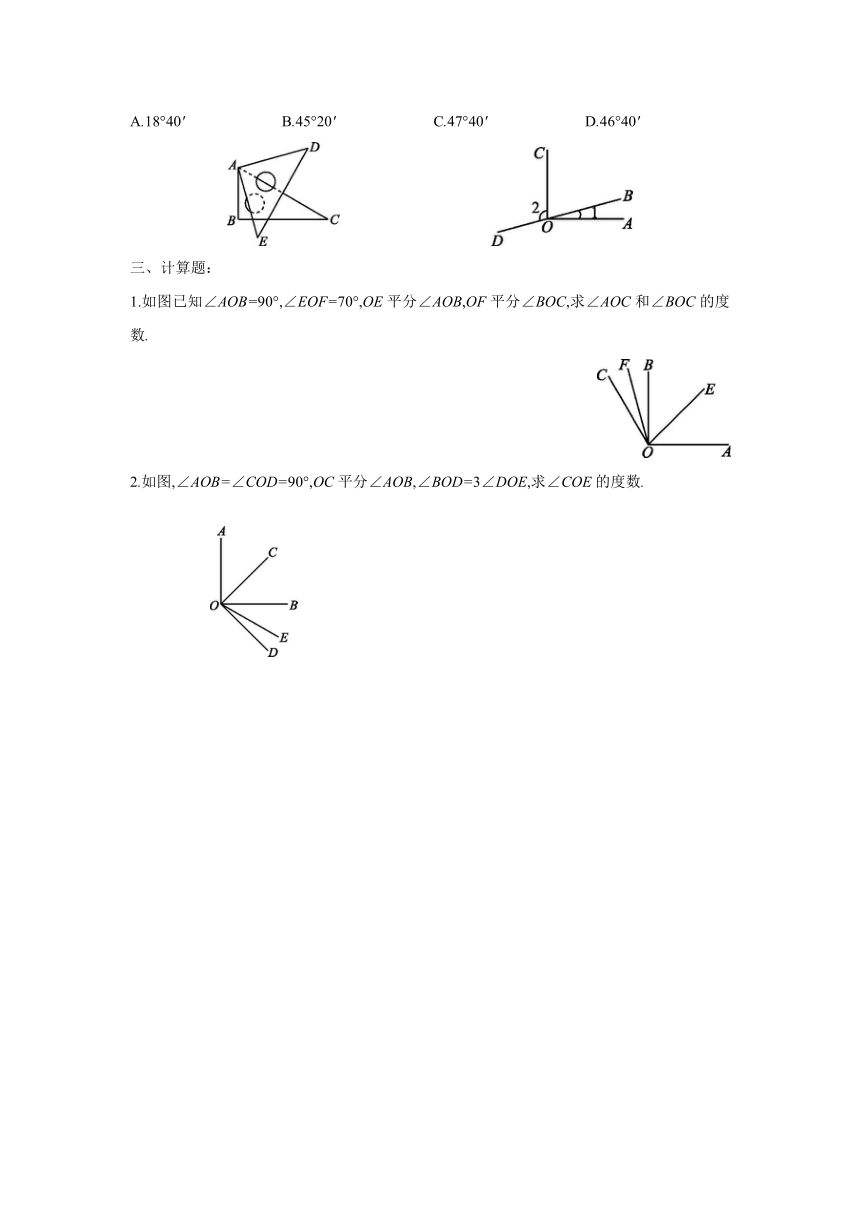
5.如图是一副三角尺的摆放图,将一个三角尺60°角的顶点与另一个三角尺的直角顶点重合,∠BAE=14°40',则∠CAD的大小是 ( )
A.18°40' B.45°20' C.47°40' D.46°40'
计算题:
1.如图已知∠AOB=90°,∠EOF=70°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠BOC的度数.
2.如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,求∠COE的度数.
参考答案与解析
一、
1.121°10′ 解析: 48 38′+72 32′ =120°70′=121°10′
2.46°19′ 解析: 105 17 ′-58 58 ′= 104 77 ′-58 58 ′=46°19 ′
3.483°20′ 解析:60 25 ′×8=480°200′=483°20′
4.11°42′ 解析:58 30 ′÷5
=58 ÷5+30′
=11°+(3°+30′)÷5
=11°+(210′÷5)
=11°+42′
=11°42′
5.91°31′30" 解析:25 25′25″+65 65′65″=90°90′90"=91°31′30"
6.139°41′8" 解析:175 -35 18′52 ″=174°59′60"-35 18′52 ″=139°41′8"
7.156°26′40" 解析:31 17′20 ″ ×5 =155°85′100"=156°26′40"
8.8°13′28" 解析:41 17′20 ″÷5
=41 ÷5+(17′20 ″÷5)
=8°+1°+(17′20 ″÷5)
=8°+(67′÷5)+20 ″÷5
=8°+13′+2′+20 ″÷5
=8°+13′+140 ″÷5
=8°+13′+28"
=8°13′28"
二、
1.B
2.C
3.C
[解析] 如图,若OC在∠AOB内部,则∠BOC1=∠AOB-∠AOC1=80°-52°=28°;
若OC在∠AOB外部,则∠BOC2=∠AOB+∠AOC2=80°+52°=132°.
4.C [解析] 当OC在∠AOB内部时,如图①,
则∠BOC=∠AOB-∠AOC=60°-×60°=30°.
因为射线OD平分∠BOC,
所以∠COD=∠BOC=15°;
当OC在∠AOB外部时,如图②,
则∠BOC=∠AOB+∠AOC=60°+×60°=90°.
因为射线OD平分∠BOC,
所以∠COD=∠BOC=45°.
综上,∠COD的度数为15°或45°.故选C.
5.B 因为∠BAC=60°,∠BAE=15°40',
所以∠EAC=44°20'.
因为∠EAD=90°,
所以∠CAD=90°-∠EAC=90°-44°20'=45°40'.
三、1.解:因为OE平分∠AOB,OF平分∠BOC,
所以∠BOE=∠AOB=×90°=45°,
∠COF=∠BOF=∠BOC.
因为∠BOF=∠EOF-∠BOE=70°-45°=25°,
所以∠BOC=2∠BOF=50°.
所以∠AOC=∠BOC+∠AOB=50°+90°=140°.
2.解:因为∠AOB=90°,OC平分∠AOB,
所以∠BOC=∠AOB=45°.
因为∠BOD=∠COD-∠BOC=90°-45°=45°,∠BOD=3∠DOE,所以∠DOE=15°.
所以∠COE=∠COD-∠DOE=90°-15°=75°.
一、计算题
1. 48 38′+72 32′ 2. 105 17 ′-58 58 ′
3.60 25 ′×8 4. 58 30 ′÷5
5.25 25′25″+65 65′65″ 6.175 -35 18′52 ″
7. 31 17′20 ″ ×5 8. 41 17′20 ″÷5
二、选择题
1.如图,在∠AOB内部任作一条射线OC,则下列结论一定成立的是( )
A.∠AOC>∠BOC B.∠BOC<∠AOB
C.∠AOC<∠BOC D.∠BOC>∠AOB
2.∠1和∠2的顶点和一边都重合,另一边都在公共边的同侧,且∠1>∠2,那么∠1的另一边落在∠2的 ( )
A.另一边上 B.内部
C.外部 D.内部或另一边上
3.已知∠AOB=80°,以O为端点作射线OC,使∠AOC=52°,则∠BOC的度数为 ( )
A.28° B.132° C.28°或132° D.68°
4.已知∠AOB=60°,∠AOC=∠AOB,射线OD平分∠BOC,则∠COD的度数为 ( )
A.15° B.45° C.15°或45° D.20°或40°
5.如图是一副三角尺的摆放图,将一个三角尺60°角的顶点与另一个三角尺的直角顶点重合,∠BAE=14°40',则∠CAD的大小是 ( )
A.18°40' B.45°20' C.47°40' D.46°40'
计算题:
1.如图已知∠AOB=90°,∠EOF=70°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠BOC的度数.
2.如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,求∠COE的度数.
参考答案与解析
一、
1.121°10′ 解析: 48 38′+72 32′ =120°70′=121°10′
2.46°19′ 解析: 105 17 ′-58 58 ′= 104 77 ′-58 58 ′=46°19 ′
3.483°20′ 解析:60 25 ′×8=480°200′=483°20′
4.11°42′ 解析:58 30 ′÷5
=58 ÷5+30′
=11°+(3°+30′)÷5
=11°+(210′÷5)
=11°+42′
=11°42′
5.91°31′30" 解析:25 25′25″+65 65′65″=90°90′90"=91°31′30"
6.139°41′8" 解析:175 -35 18′52 ″=174°59′60"-35 18′52 ″=139°41′8"
7.156°26′40" 解析:31 17′20 ″ ×5 =155°85′100"=156°26′40"
8.8°13′28" 解析:41 17′20 ″÷5
=41 ÷5+(17′20 ″÷5)
=8°+1°+(17′20 ″÷5)
=8°+(67′÷5)+20 ″÷5
=8°+13′+2′+20 ″÷5
=8°+13′+140 ″÷5
=8°+13′+28"
=8°13′28"
二、
1.B
2.C
3.C
[解析] 如图,若OC在∠AOB内部,则∠BOC1=∠AOB-∠AOC1=80°-52°=28°;
若OC在∠AOB外部,则∠BOC2=∠AOB+∠AOC2=80°+52°=132°.
4.C [解析] 当OC在∠AOB内部时,如图①,
则∠BOC=∠AOB-∠AOC=60°-×60°=30°.
因为射线OD平分∠BOC,
所以∠COD=∠BOC=15°;
当OC在∠AOB外部时,如图②,
则∠BOC=∠AOB+∠AOC=60°+×60°=90°.
因为射线OD平分∠BOC,
所以∠COD=∠BOC=45°.
综上,∠COD的度数为15°或45°.故选C.
5.B 因为∠BAC=60°,∠BAE=15°40',
所以∠EAC=44°20'.
因为∠EAD=90°,
所以∠CAD=90°-∠EAC=90°-44°20'=45°40'.
三、1.解:因为OE平分∠AOB,OF平分∠BOC,
所以∠BOE=∠AOB=×90°=45°,
∠COF=∠BOF=∠BOC.
因为∠BOF=∠EOF-∠BOE=70°-45°=25°,
所以∠BOC=2∠BOF=50°.
所以∠AOC=∠BOC+∠AOB=50°+90°=140°.
2.解:因为∠AOB=90°,OC平分∠AOB,
所以∠BOC=∠AOB=45°.
因为∠BOD=∠COD-∠BOC=90°-45°=45°,∠BOD=3∠DOE,所以∠DOE=15°.
所以∠COE=∠COD-∠DOE=90°-15°=75°.
