浙江省S9联盟2021-2022学年高二上学期期中联考数学试题(Word版含答案)
文档属性
| 名称 | 浙江省S9联盟2021-2022学年高二上学期期中联考数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 555.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 19:41:32 | ||
图片预览



文档简介
绝密★考试结束前
浙江省S9联盟2021-2022学年高二上学期期中联考
数学学科 试题
考生须知:
本卷共4页满分150分,考试时间120分钟;
答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字;
所有答案必须写在答题纸上,写在试卷上无效;
考试结束后,只需上交答题纸.
第Ⅰ卷(选择题)
一、单选题(每题5分,共40分)
1.已知为虚数单位,则复数的实部是( )
A. B. C. D.
2.已知实数,,则下列不等式恒成立的是( )
A. B. C. D.
3.为迎接2022年杭州亚运会,亚委会采用按性别分层随机抽样的方法从某高校报名的200名学生志愿者中抽取30人组成亚运志愿小组,若30人中共有男生12人,则这200名学生志愿者中男生可能有( )人
A.18 B.12 C.120 D.80
4.若向量,则( )
A. B. C.∥ D.
5.将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为( )
A. B. C. D.
6.设是两个不同平面,是两条直线,下列命题中正确的是( )
A.如果,,,那么∥
B.如果,,∥,那么
C.如果∥,,,那么∥
D.如果∥,与所成的角和与所成的角相等,那么∥
7.设,则“”是“”的( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分又不必要条件
8.在等腰梯形中,∥是腰上的动点,则的最小值为( )
A. B.3 C. D.
二、多选题(每题5分,少选得2分,多选或错选得0分,共20分)
9.给定一组数5,5,4,3,3,3,2,2,2,1,则( )
A.平均数为3 B.标准差为
C.众数为2和3 D.85%分位数为4.5
10.抛掷三枚硬币,设事件“第枚硬币正面朝上”,.则( )
A.与互斥 B.与相互独立
C. D.
11.以下结论正确的是( )
A.
B.的最小值为
C.若则
D.若则 (第12题图)
12.如图,三棱柱的各棱长均为2,侧棱与底面所成的角为60°,为锐角,且侧面底面,下列四个结
论正确的是( )
A.° B.
C.直线与平面所成的角为° D.
第II卷(非选择题)
三、填空题(每题5分,共20分)
13.甲、乙两人独立地破译一份密码,已知各人能破译的概率分别为则密码被成功破译的概率_________.
14.已知函数,则的零点个数为________.
15.若不等式对于一切恒成立,则实数的取值范围为______.
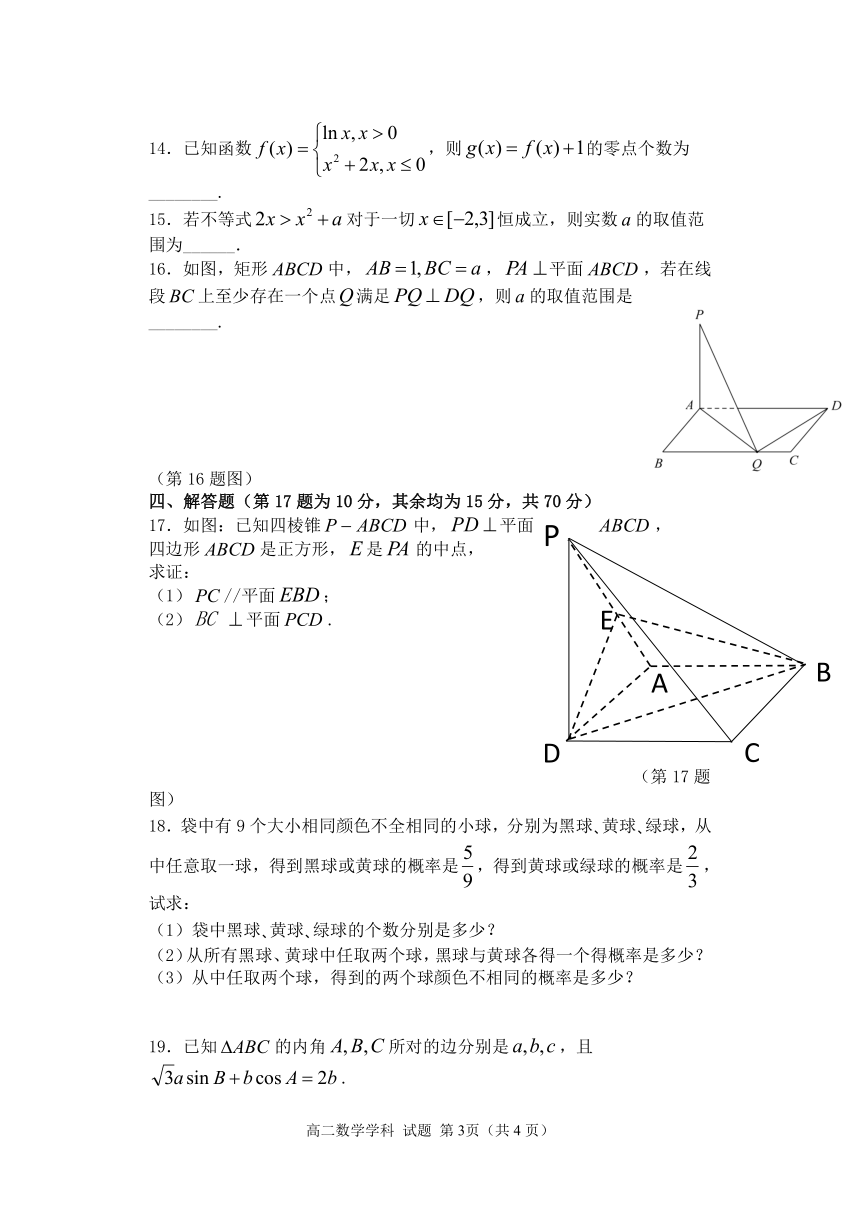
16.如图,矩形中,,平面,若在线段上至少存在一个点满足,则的取值范围是________.
(第16题图)
四、解答题(第17题为10分,其余均为15分,共70分)
17.如图:已知四棱锥中,平面,
四边形是正方形,是的中点,
求证:
(1)//平面;
(2)平面.
(第17题图)
18.袋中有9个大小相同颜色不全相同的小球,分别为黑球 黄球 绿球,从中任意取一球,得到黑球或黄球的概率是,得到黄球或绿球的概率是,试求:
(1)袋中黑球 黄球 绿球的个数分别是多少?
(2)从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是多少?
(3)从中任取两个球,得到的两个球颜色不相同的概率是多少?
19.已知的内角所对的边分别是,且.
(1)求角的大小;
(2)若且的面积,求
20. 已知定义在上的函数.
(1)求的值,并判断的奇偶性(要有过程);
(2)当时,不等式恒成立,求实数的取值范围.
21.在三棱柱中,,,,平面,是的中点.
(1)求证:平面平面;
(2)求直线与平面所成角的正弦值.
(第21题图)
参考答案
单选题
题号 1 2 3 4 5 6 7 8
答案 B C D D A C A C
8.C
【详解】
解:如图,以为原点,射线为轴正半轴建立直角坐标系,则由题意可得,设,其,
则,
所以,
所以
,
所以当时,取最小值, 故选:C
多选题
题号 9 10 11 12
答案 AC BCD AC ACD
13.ACD【详解】
如图,过作,为垂足,连结,
如图建立空间直角坐标系
对于A选项,侧棱与底面所成角为,为锐角,
且侧面底面,,又三棱柱的各棱长相等,可知四边形为菱形,,
故A选项正确;
对于B选项,易知
,故B选项不正确;
对于C选项,由题意可知即为与平面所成的角,
,,故C选项正确;
对于D选项,,
因此,故D选项正确.
故选:ACD
三、填空题
13. 14.2 15. 16.
四、解答题
17.(1)证明见解析(2)证明见解析
【分析】
(1)连BD,与AC交于O,利用三角形的中位线,可得线线平行,从而可得线面平行;
(2)先证明,,从而可证BC⊥平面PCD
【详解】
(1)连,与交于,连接
∵是正方形,∴是的中点,
∵是的中点,∴
又∵平面,平面
∴平面; 5分
(2)∵平面,平面∴
∵是正方形,∴又∵
∴平面 5分
18.(1)黑球 黄球 绿球的分别有3、2、4个; 5分(对1个2分,对2个5分)
(2)0.6 5分
(3). 5分
19.(1);(2).
【分析】
(1)由正弦定理结合辅助角公式得出角A的大小;
(2)利用面积公式以及余弦定理,解出的值.
【详解】
(1)因为,由正弦定理得;
2分
所以
得 5分
因
故 7分
(2) 9分
得
12分
所以 15分
20.(1), 为奇函数, 7分
(2)由,得,
因为,所以,
所以.
令,则,此时不等式可化为,
记,因为当时,和均为减函数,
所以为减函数,故,
因为恒成立,所以. 15分
21.(1)证明见解析;(2).
【详解】
(1)由平面,平面,得, 2分
又,,故平面, 4分
平面,故平面平面. 6分
(2)以为原点,为轴,为轴,建立如图所示空间直角坐标系,
则,, 8分
又,,
故,,,
,
设平面的一个法向量为,则
,即,令,则, , 11分
设直线与平面所成的角为,
故, 15分
即直线与平面所成角的正弦值为.
高二数学学科 试题 第1页(共4页)
浙江省S9联盟2021-2022学年高二上学期期中联考
数学学科 试题
考生须知:
本卷共4页满分150分,考试时间120分钟;
答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字;
所有答案必须写在答题纸上,写在试卷上无效;
考试结束后,只需上交答题纸.
第Ⅰ卷(选择题)
一、单选题(每题5分,共40分)
1.已知为虚数单位,则复数的实部是( )
A. B. C. D.
2.已知实数,,则下列不等式恒成立的是( )
A. B. C. D.
3.为迎接2022年杭州亚运会,亚委会采用按性别分层随机抽样的方法从某高校报名的200名学生志愿者中抽取30人组成亚运志愿小组,若30人中共有男生12人,则这200名学生志愿者中男生可能有( )人
A.18 B.12 C.120 D.80
4.若向量,则( )
A. B. C.∥ D.
5.将棱长为2的正方体木块削成一个体积最大的球,则该球的体积为( )
A. B. C. D.
6.设是两个不同平面,是两条直线,下列命题中正确的是( )
A.如果,,,那么∥
B.如果,,∥,那么
C.如果∥,,,那么∥
D.如果∥,与所成的角和与所成的角相等,那么∥
7.设,则“”是“”的( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分又不必要条件
8.在等腰梯形中,∥是腰上的动点,则的最小值为( )
A. B.3 C. D.
二、多选题(每题5分,少选得2分,多选或错选得0分,共20分)
9.给定一组数5,5,4,3,3,3,2,2,2,1,则( )
A.平均数为3 B.标准差为
C.众数为2和3 D.85%分位数为4.5
10.抛掷三枚硬币,设事件“第枚硬币正面朝上”,.则( )
A.与互斥 B.与相互独立
C. D.
11.以下结论正确的是( )
A.
B.的最小值为
C.若则
D.若则 (第12题图)
12.如图,三棱柱的各棱长均为2,侧棱与底面所成的角为60°,为锐角,且侧面底面,下列四个结
论正确的是( )
A.° B.
C.直线与平面所成的角为° D.
第II卷(非选择题)
三、填空题(每题5分,共20分)
13.甲、乙两人独立地破译一份密码,已知各人能破译的概率分别为则密码被成功破译的概率_________.
14.已知函数,则的零点个数为________.
15.若不等式对于一切恒成立,则实数的取值范围为______.
16.如图,矩形中,,平面,若在线段上至少存在一个点满足,则的取值范围是________.
(第16题图)
四、解答题(第17题为10分,其余均为15分,共70分)
17.如图:已知四棱锥中,平面,
四边形是正方形,是的中点,
求证:
(1)//平面;
(2)平面.
(第17题图)
18.袋中有9个大小相同颜色不全相同的小球,分别为黑球 黄球 绿球,从中任意取一球,得到黑球或黄球的概率是,得到黄球或绿球的概率是,试求:
(1)袋中黑球 黄球 绿球的个数分别是多少?
(2)从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是多少?
(3)从中任取两个球,得到的两个球颜色不相同的概率是多少?
19.已知的内角所对的边分别是,且.
(1)求角的大小;
(2)若且的面积,求
20. 已知定义在上的函数.
(1)求的值,并判断的奇偶性(要有过程);
(2)当时,不等式恒成立,求实数的取值范围.
21.在三棱柱中,,,,平面,是的中点.
(1)求证:平面平面;
(2)求直线与平面所成角的正弦值.
(第21题图)
参考答案
单选题
题号 1 2 3 4 5 6 7 8
答案 B C D D A C A C
8.C
【详解】
解:如图,以为原点,射线为轴正半轴建立直角坐标系,则由题意可得,设,其,
则,
所以,
所以
,
所以当时,取最小值, 故选:C
多选题
题号 9 10 11 12
答案 AC BCD AC ACD
13.ACD【详解】
如图,过作,为垂足,连结,
如图建立空间直角坐标系
对于A选项,侧棱与底面所成角为,为锐角,
且侧面底面,,又三棱柱的各棱长相等,可知四边形为菱形,,
故A选项正确;
对于B选项,易知
,故B选项不正确;
对于C选项,由题意可知即为与平面所成的角,
,,故C选项正确;
对于D选项,,
因此,故D选项正确.
故选:ACD
三、填空题
13. 14.2 15. 16.
四、解答题
17.(1)证明见解析(2)证明见解析
【分析】
(1)连BD,与AC交于O,利用三角形的中位线,可得线线平行,从而可得线面平行;
(2)先证明,,从而可证BC⊥平面PCD
【详解】
(1)连,与交于,连接
∵是正方形,∴是的中点,
∵是的中点,∴
又∵平面,平面
∴平面; 5分
(2)∵平面,平面∴
∵是正方形,∴又∵
∴平面 5分
18.(1)黑球 黄球 绿球的分别有3、2、4个; 5分(对1个2分,对2个5分)
(2)0.6 5分
(3). 5分
19.(1);(2).
【分析】
(1)由正弦定理结合辅助角公式得出角A的大小;
(2)利用面积公式以及余弦定理,解出的值.
【详解】
(1)因为,由正弦定理得;
2分
所以
得 5分
因
故 7分
(2) 9分
得
12分
所以 15分
20.(1), 为奇函数, 7分
(2)由,得,
因为,所以,
所以.
令,则,此时不等式可化为,
记,因为当时,和均为减函数,
所以为减函数,故,
因为恒成立,所以. 15分
21.(1)证明见解析;(2).
【详解】
(1)由平面,平面,得, 2分
又,,故平面, 4分
平面,故平面平面. 6分
(2)以为原点,为轴,为轴,建立如图所示空间直角坐标系,
则,, 8分
又,,
故,,,
,
设平面的一个法向量为,则
,即,令,则, , 11分
设直线与平面所成的角为,
故, 15分
即直线与平面所成角的正弦值为.
高二数学学科 试题 第1页(共4页)
同课章节目录
