2021—2022学年苏科版数学八年级上册 6.1.2 函数的表达方法(共20张)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级上册 6.1.2 函数的表达方法(共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 00:36:00 | ||
图片预览







文档简介
(共20张PPT)
6.1 函数(2)
问题1.正方形的面积S与边长x的取值如下表,面积S是不是边长x的函数?
这里是怎样表示正方形面积S与边长x之间的函数关系的?
列表来表示的.
1 4 9 16 25 36 49
是
新课讲解
用平面直角坐标系中的一个图象来表示的.
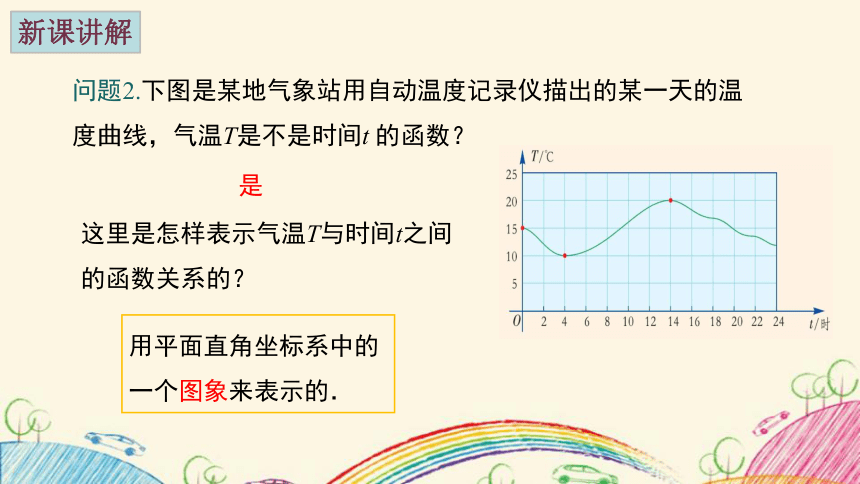
问题2.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?
这里是怎样表示气温T与时间t之间的函数关系的?
是
新课讲解
问题3.某城市居民用的天然气,1m3收费2.88元,使用x(m3) 天然气应缴纳的费用y(元)为 y = 2.88x. y是不是x 的函数?
这里是怎样表示缴纳的天然气费y与所用天然气的体积x的函数关系的?
y=2.88x来表示.
是
新课讲解
像这样表示两个变量之间函数关系的式子称为函数表达式.
函数的三种表示法:
y = 2.88x
图象法、
列表法、
表达式法.
1 4 9 16 25 36 49
知识要点
汽车以100km/h的速度匀速行驶,在这一变化过程中:
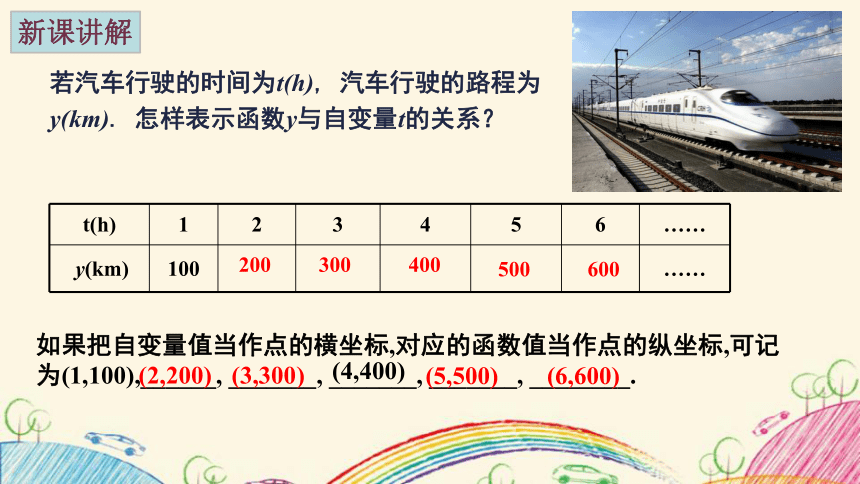
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
新课讲解
t(h) 1 2 3 4 5 6 ……
y(km) 100 ……
200
300
400
500
600
(1)可以列表来表示:
如果把自变量值当作点的横坐标,对应的函数值当作点的纵坐标,可记为(1,100),______, _______, _______, _______, ________.
(2,200)
(3,300)
(4,400)
(5,500)
(6,600)
新课讲解
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
t(h) 1 2 3 4 5 6 ……
y(km) 100 ……
200
300
400
500
600
(2)可以在坐标系中画图表示:
t(h)
O
1
100
2
3
4
y(km)
5
6
200
300
400
500
新课讲解
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图象
(3) 还可以列式表示:
y =100t.
新课讲解
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
解:汽车行驶100 km耗油10 L,
行驶 s km耗油 ,
所以 Q (L)与 s (km) 之间的函数表达式为:
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
(2)汽车行驶250km时,油箱里还有多少油?
解:当S =250时,
=15
15叫做当自变量的值为250时的函数值
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
(3)你认为这辆汽车现有油量够它行驶多远?
解:由题意得:
解得:
S=400
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
(4) s的值最小取多少?s的取值有什么范围限制吗
解:S的最小值是0.
有,是0 ≤S≤400.
在实际问题中,自变量的取值通常有一定的范围.
想一想:下列函数中自变量x的取值范围是什么?
.
0
.
-1
.
-2
-2
x取全体实数
使函数表达式有意义的自变量的全体.
2.等腰三角形中,设顶角的度数为 y ,底角的度数为 x ,则y与x之间的函数表达式是 ,自变量x的取值范围是 .
归纳:确定自变量的取值范围时,不仅要考虑使函数表达式有意义,而且还要注意问题的实际意义.
例 小明骑自行车从甲地到乙地,图中的折线表示小明的行程 s (km)与途中所花时间 t (h)之间的函数关系.试根据函数图像回答下列问题:
(1)小明从甲地到乙地用了多少时间?
解:小明从甲地到乙地用了7 h
新课讲解
例
当t=5时,s=30.小明出发5 h时,距离甲地30 km.
(2)小明出发5h时,距离甲地有多远?
(3)折线中有一条平行于t轴的线段,它的意义是什么?
当t从2变化到4时,s的值不变,说明小明在途中滞留了2 h.
新课讲解
(4)求本题中自变量t的取值范围.
0≤t≤7
练习:
甲、乙两人出门散步,用20min走了900米后,甲随即按原路返回;乙遇到一位朋友,并与朋友交谈了10min后,用15min回到家里.在下列4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)之间的函数关系?哪一个表示乙离家的路程s(m)与时间t(min)之间的函数关系?
甲
乙
通过这节课的学习,你有哪些收获?
课堂小结
谢谢~
6.1 函数(2)
问题1.正方形的面积S与边长x的取值如下表,面积S是不是边长x的函数?
这里是怎样表示正方形面积S与边长x之间的函数关系的?
列表来表示的.
1 4 9 16 25 36 49
是
新课讲解
用平面直角坐标系中的一个图象来表示的.
问题2.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?
这里是怎样表示气温T与时间t之间的函数关系的?
是
新课讲解
问题3.某城市居民用的天然气,1m3收费2.88元,使用x(m3) 天然气应缴纳的费用y(元)为 y = 2.88x. y是不是x 的函数?
这里是怎样表示缴纳的天然气费y与所用天然气的体积x的函数关系的?
y=2.88x来表示.
是
新课讲解
像这样表示两个变量之间函数关系的式子称为函数表达式.
函数的三种表示法:
y = 2.88x
图象法、
列表法、
表达式法.
1 4 9 16 25 36 49
知识要点
汽车以100km/h的速度匀速行驶,在这一变化过程中:
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
新课讲解
t(h) 1 2 3 4 5 6 ……
y(km) 100 ……
200
300
400
500
600
(1)可以列表来表示:
如果把自变量值当作点的横坐标,对应的函数值当作点的纵坐标,可记为(1,100),______, _______, _______, _______, ________.
(2,200)
(3,300)
(4,400)
(5,500)
(6,600)
新课讲解
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
t(h) 1 2 3 4 5 6 ……
y(km) 100 ……
200
300
400
500
600
(2)可以在坐标系中画图表示:
t(h)
O
1
100
2
3
4
y(km)
5
6
200
300
400
500
新课讲解
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图象
(3) 还可以列式表示:
y =100t.
新课讲解
若汽车行驶的时间为t(h), 汽车行驶的路程为y(km). 怎样表示函数y与自变量t的关系?
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
解:汽车行驶100 km耗油10 L,
行驶 s km耗油 ,
所以 Q (L)与 s (km) 之间的函数表达式为:
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
(2)汽车行驶250km时,油箱里还有多少油?
解:当S =250时,
=15
15叫做当自变量的值为250时的函数值
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
(3)你认为这辆汽车现有油量够它行驶多远?
解:由题意得:
解得:
S=400
问题3. 汽车油箱内存油40L,每行驶100km耗油10L.
(1)求行驶过程中油箱内剩余油量 Q(L)与行驶路程 s(km) 的函数表达式.
自学互助
(4) s的值最小取多少?s的取值有什么范围限制吗
解:S的最小值是0.
有,是0 ≤S≤400.
在实际问题中,自变量的取值通常有一定的范围.
想一想:下列函数中自变量x的取值范围是什么?
.
0
.
-1
.
-2
-2
x取全体实数
使函数表达式有意义的自变量的全体.
2.等腰三角形中,设顶角的度数为 y ,底角的度数为 x ,则y与x之间的函数表达式是 ,自变量x的取值范围是 .
归纳:确定自变量的取值范围时,不仅要考虑使函数表达式有意义,而且还要注意问题的实际意义.
例 小明骑自行车从甲地到乙地,图中的折线表示小明的行程 s (km)与途中所花时间 t (h)之间的函数关系.试根据函数图像回答下列问题:
(1)小明从甲地到乙地用了多少时间?
解:小明从甲地到乙地用了7 h
新课讲解
例
当t=5时,s=30.小明出发5 h时,距离甲地30 km.
(2)小明出发5h时,距离甲地有多远?
(3)折线中有一条平行于t轴的线段,它的意义是什么?
当t从2变化到4时,s的值不变,说明小明在途中滞留了2 h.
新课讲解
(4)求本题中自变量t的取值范围.
0≤t≤7
练习:
甲、乙两人出门散步,用20min走了900米后,甲随即按原路返回;乙遇到一位朋友,并与朋友交谈了10min后,用15min回到家里.在下列4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)之间的函数关系?哪一个表示乙离家的路程s(m)与时间t(min)之间的函数关系?
甲
乙
通过这节课的学习,你有哪些收获?
课堂小结
谢谢~
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
