2021-2022学年人教版八年级数学上册 13.1.1轴对称(共19张)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册 13.1.1轴对称(共19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 825.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 00:39:46 | ||
图片预览





文档简介
(共19张PPT)
八年级上册
13.1.1 轴对称
1、认识轴对称和轴对称图形,并能找出对称轴;
2、知道轴对称和轴对称图形的区别和联系.
学习目标
1、轴对称图形定义:把—个图形沿着某—条直线_____,直线两旁的部份能够互相_______,这个图形就是轴对称图形。折痕所在的这条直线叫做_________,折叠后重合的点是对应点,叫做 .
2、经过线段中点并且垂直于这条线段的直线,叫做这条线段的 ,如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的 .
3、轴对称定义:把一个图形沿着某一条直线_______,如果这个图形能够与另一个图形重合,那么这两个图形关于这条直线成_________,这条直线叫做_________。两个图形中的对应点叫_________。
4、下面的数字、字母和汉字中,哪些是轴对称图形?
0 、6、9、3、A、F、D、G、中、由、用、甲、工、月、田、水
是轴对称图形的是__________________________________________________。
折叠
重合
对称轴
对称轴
垂直平分线
折叠
对称
对称轴
对称点
0 、3、A、D、中、由、甲、工、田
对称点
预习反馈
探究点一
1.把—张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的图案。观察得到的图案,你能发现它们有什么?
结论: 如果一个平面图形沿一条直线 ,直线两旁的部分能够互相 ,这个图形就叫做轴对称图形,这条直线就是它的对称轴。
折叠
重合
合作探究
探究点一
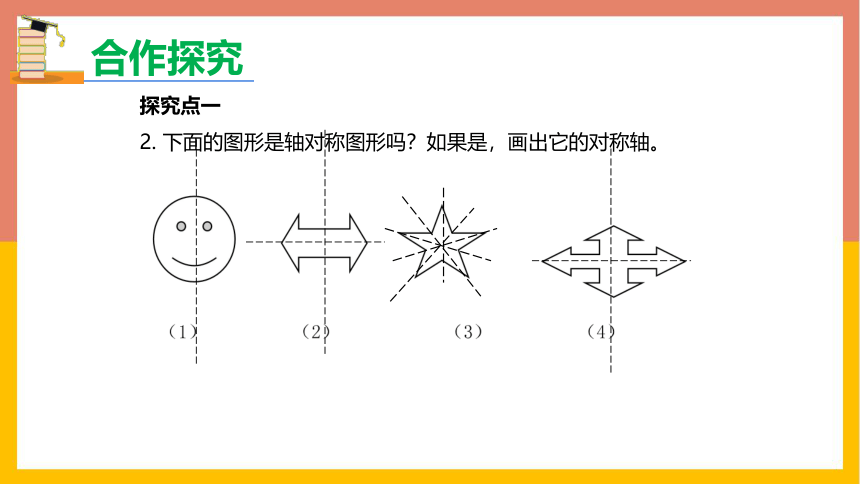
2. 下面的图形是轴对称图形吗?如果是,画出它的对称轴。
合作探究
探究点二
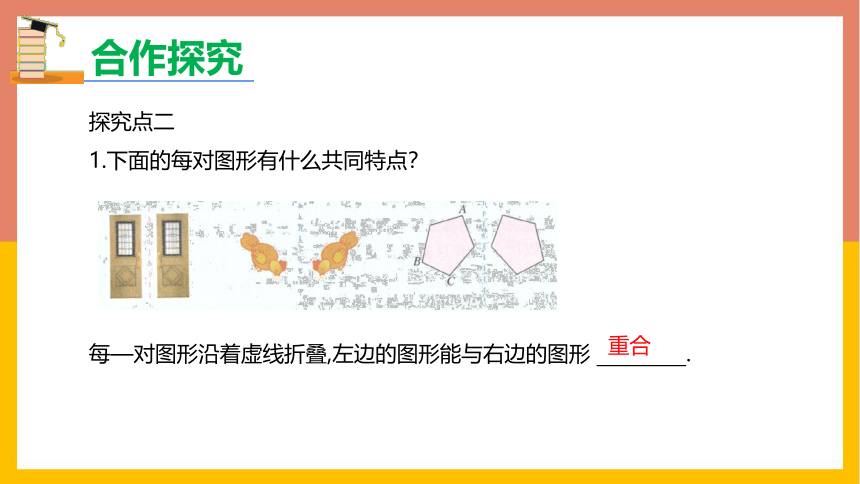
1.下面的每对图形有什么共同特点?
每—对图形沿着虚线折叠,左边的图形能与右边的图形 .
重合
合作探究
探究点二
1.下面的每对图形有什么共同特点?
每—对图形沿着虚线折叠,左边的图形能与右边的图形 .
重合
合作探究
探究点二
2. 下面给出的每幅图中的两个图案是轴对称的吗?如果是,试着找出它们的对称轴,并找出一对对称点.
合作探究
探究点三
1.成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
2. 把成轴对称的两个图形看成—个整体,它就是—个_____________;把—个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴_____________.
轴对称图形
对称
合作探究
探究点四
1.如图△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′ 分别是点A,B,C的对称点,线段AA′ ,BB′ ,CC′ 与直线MN有什么关系
2.两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的___________ ;轴对称图形的对称轴是任何一对对应点所连线段的_____________.
垂直平分线
点A,A′ 是对称点,设AA′ 交对称轴MN于点P,
△ABC或△A′B′C′沿MN折叠后,点A与A′重合。于是有
AP=PA′, ∠ MPA=∠MPA′ =90°。
对于其他的对应点,如点B与B ′点C与C′也有类似的情况.
因此,对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
垂直平分线
合作探究
1. 如图是由小正方形组成的L形图,若在图中添加一个小正方形,使它成为轴对称图形,有______种方法.
解:共3种方法,如图.
3
例题解析
2. 如图,将一块正方形纸片沿对角线折叠一次,在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )
A
B
C
D
C
合作探究
1、轴对称图形的对称轴的条数( )
A.只有1条 2条 C.3条 D.至少一条
2、下列图形中对称轴最多的是( )
A.圆 B.正方形 C.角 D.线段
3、如下图,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.
答:图形 ;理由是: .
D
A
②
其余三个都是轴对称图形
随堂检测
4、标出下列图形中点A、B、C的对称点。
A′
B′
C′
A′
B′
C′
随堂检测
5、下列图形是否是轴对称图形,如果是,找出轴对称图形的所有对称轴。
不是
是
是
不是
是
随堂检测
6.正三角形有 条对称轴;正四边形有 条对称轴; 正五边形有 条对称轴;正六边形有 条对称轴;正n边形有 条对称轴;
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
当n越来越大时,正多边形接近于圆,圆有无数条对称轴。
三
四
五
六
n
随堂检测
1.轴对称图形定义
2. 轴对称定义
3. 轴对称图形与两个图形成轴对称的联系与区别
4. 轴对称的性质
课堂小结
书面作业:完成相关书本作业
布置作业
数学活动:
找一找你身边有哪些轴对称图形
再见
八年级上册
13.1.1 轴对称
1、认识轴对称和轴对称图形,并能找出对称轴;
2、知道轴对称和轴对称图形的区别和联系.
学习目标
1、轴对称图形定义:把—个图形沿着某—条直线_____,直线两旁的部份能够互相_______,这个图形就是轴对称图形。折痕所在的这条直线叫做_________,折叠后重合的点是对应点,叫做 .
2、经过线段中点并且垂直于这条线段的直线,叫做这条线段的 ,如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的 .
3、轴对称定义:把一个图形沿着某一条直线_______,如果这个图形能够与另一个图形重合,那么这两个图形关于这条直线成_________,这条直线叫做_________。两个图形中的对应点叫_________。
4、下面的数字、字母和汉字中,哪些是轴对称图形?
0 、6、9、3、A、F、D、G、中、由、用、甲、工、月、田、水
是轴对称图形的是__________________________________________________。
折叠
重合
对称轴
对称轴
垂直平分线
折叠
对称
对称轴
对称点
0 、3、A、D、中、由、甲、工、田
对称点
预习反馈
探究点一
1.把—张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的图案。观察得到的图案,你能发现它们有什么?
结论: 如果一个平面图形沿一条直线 ,直线两旁的部分能够互相 ,这个图形就叫做轴对称图形,这条直线就是它的对称轴。
折叠
重合
合作探究
探究点一
2. 下面的图形是轴对称图形吗?如果是,画出它的对称轴。
合作探究
探究点二
1.下面的每对图形有什么共同特点?
每—对图形沿着虚线折叠,左边的图形能与右边的图形 .
重合
合作探究
探究点二
1.下面的每对图形有什么共同特点?
每—对图形沿着虚线折叠,左边的图形能与右边的图形 .
重合
合作探究
探究点二
2. 下面给出的每幅图中的两个图案是轴对称的吗?如果是,试着找出它们的对称轴,并找出一对对称点.
合作探究
探究点三
1.成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
2. 把成轴对称的两个图形看成—个整体,它就是—个_____________;把—个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴_____________.
轴对称图形
对称
合作探究
探究点四
1.如图△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′ 分别是点A,B,C的对称点,线段AA′ ,BB′ ,CC′ 与直线MN有什么关系
2.两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的___________ ;轴对称图形的对称轴是任何一对对应点所连线段的_____________.
垂直平分线
点A,A′ 是对称点,设AA′ 交对称轴MN于点P,
△ABC或△A′B′C′沿MN折叠后,点A与A′重合。于是有
AP=PA′, ∠ MPA=∠MPA′ =90°。
对于其他的对应点,如点B与B ′点C与C′也有类似的情况.
因此,对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
垂直平分线
合作探究
1. 如图是由小正方形组成的L形图,若在图中添加一个小正方形,使它成为轴对称图形,有______种方法.
解:共3种方法,如图.
3
例题解析
2. 如图,将一块正方形纸片沿对角线折叠一次,在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )
A
B
C
D
C
合作探究
1、轴对称图形的对称轴的条数( )
A.只有1条 2条 C.3条 D.至少一条
2、下列图形中对称轴最多的是( )
A.圆 B.正方形 C.角 D.线段
3、如下图,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.
答:图形 ;理由是: .
D
A
②
其余三个都是轴对称图形
随堂检测
4、标出下列图形中点A、B、C的对称点。
A′
B′
C′
A′
B′
C′
随堂检测
5、下列图形是否是轴对称图形,如果是,找出轴对称图形的所有对称轴。
不是
是
是
不是
是
随堂检测
6.正三角形有 条对称轴;正四边形有 条对称轴; 正五边形有 条对称轴;正六边形有 条对称轴;正n边形有 条对称轴;
当n越来越大时,正多边形接近于什么图形?它有多少条对称轴?
当n越来越大时,正多边形接近于圆,圆有无数条对称轴。
三
四
五
六
n
随堂检测
1.轴对称图形定义
2. 轴对称定义
3. 轴对称图形与两个图形成轴对称的联系与区别
4. 轴对称的性质
课堂小结
书面作业:完成相关书本作业
布置作业
数学活动:
找一找你身边有哪些轴对称图形
再见
