数学五年级下青岛版五年制3.2.2《圆锥的体积》课件
文档属性
| 名称 | 数学五年级下青岛版五年制3.2.2《圆锥的体积》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-27 16:25:00 | ||
图片预览






文档简介
(共41张PPT)
主页
复习
课题
实验
例1
即时训练
想一想
练习
选择
圆锥的特征
1、同桌说一说圆柱体积的计算公式。
(1)已知 s、h 求 v
(2)已知 r、h 求 v
(3)已知 d、h 求 v
主页
计算体积
蛋筒
铅锤
沙 堆
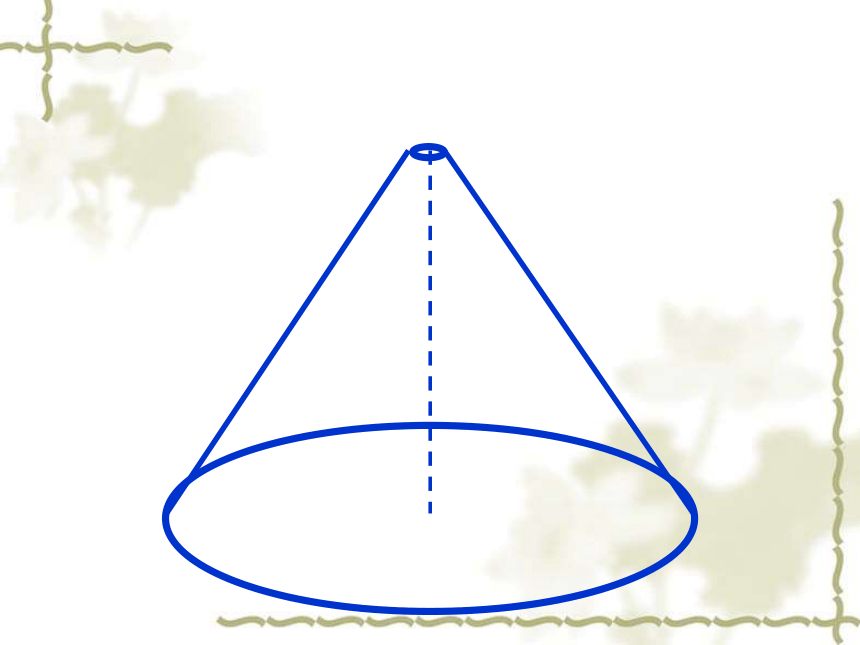
从圆锥的顶点到圆心的距离是圆锥的高
顶点
底面
高
侧面
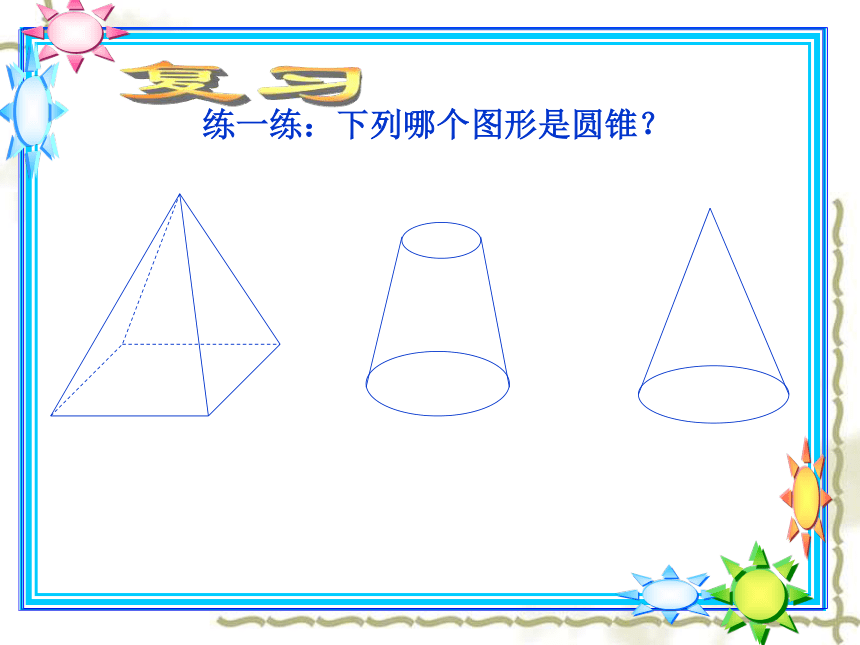
练一练:下列哪个图形是圆锥?
异同点
主页
1、说一说圆锥有哪些特征?
(1)顶部:尖顶;
(2)底面:是一个圆;
(3)侧面:是一个曲面(展开是一个扇形);
(4)底面圆周上任一点与顶点之间的距离都相等。
(5)高只有一条。
想一想:
圆柱和圆锥的底和高有什么关系
圆柱和圆锥等底等高
你发现了什么
圆柱的体积是与它等底等高圆锥体积的3倍.
圆柱体积=底面积 高
圆柱体积=底面积 高
圆柱体积=底面积 高
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
底面积 高
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
实验报告表
实验器材
一桶水、等底等高
的圆柱和圆锥各一个
实验过程
①在空圆柱里满水倒入空圆锥里,( )次正好倒完。
在空圆锥里装 满水倒入空圆里,( )次正好装满。
结 论
②圆柱的体积是和它( )的圆锥体积的( )倍。
圆锥体积
计算公式
V=
②圆锥的体积是和它( )
的圆柱体积的
实 验 报 告 表
3
3
等底等高
等底等高
3
3
1
3
1
S h
主页
思考
思考
主页
要求圆锥的体积,必须知道
哪两个条件?为什么要乘
3
1
例1
例1 一个圆锥体,底面积是7.8平方分米,
高是1.8分米。这个圆锥的体积是多少
主页
V=1/3Sh
=1/3×7.8×1.8
=2.6×1.8
=4.68(平方分米)
答:这个圆锥的体积是4.68平方分米。
等底等高
1
24
×底面积×高
V= s h
一、填空:
1、圆锥的体积=( ),用字母表示是( )。
2、圆柱体积的 与和它( )的圆锥的体积相等。
3、一个圆柱和一个圆锥等底等高,圆柱的体积是3立方分米,圆锥的体积是( )立方分米。
4、一个圆锥的底面积是12平方厘米,高是6厘米,体积是( )立方厘米。
二、判断:
1、圆柱体的体积一定比圆锥体的体积大( )
2、圆锥的体积等于和它等底等高的圆柱体的 ( )
3、正方体、长方体、圆锥体的体积都等于底面积×高。 ( )
4、等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米。( )
√
×
√
×
即时训练
练一练 1、求下面各圆锥的体积。
(1)圆锥的底面积是0.9平方米,高是0.5米。 它的体积是多少立方米?
V=1/3Sh
=1/3×0.9×0.5
=0.3×0.5
=0.15(平方米)
答:它的体积是0.15平方米。
主页
如果已知圆锥的高和底面半径
(或直径、周长),怎样求圆锥的
体积呢?
想一想
主页
练习1
1、求下面各圆锥的体积。
(2)底面半径是2 厘米,高3厘米。
(3)底面直径是6分米,高6分米 。
巩 固 练 习
主页
1
2
3
练习2
巩 固 练 习
2、求下面各圆锥的体积。(单位:厘米)
(1) (2)
7 8 10
3
主页
1
2
3
练习3
思 考:
1、一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 18 立方米,
圆柱的体积是( )。
2、一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 12 厘米, 圆锥的
高是( )。
3、一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 314 平方米,
圆锥的底面积是( )。
主页
1
2
3
54 立方米
36 厘米
942 平方米
三:选择题
主页
1:一个圆柱的体积比与它等地等高圆锥体积多12立方厘米,这个圆锥体积是( )立方厘米。
A . 4 B.3 C. 6 D.9
2:一个圆锥和一个圆柱的相等,圆锥的底面半径是圆柱底面半径的2倍,那么圆锥体积是圆柱体积的( )
9倍
3倍
3
4
倍
A
B
C
C
A
主页
复习
课题
实验
例1
即时训练
想一想
练习
选择
圆锥的特征
1、同桌说一说圆柱体积的计算公式。
(1)已知 s、h 求 v
(2)已知 r、h 求 v
(3)已知 d、h 求 v
主页
计算体积
蛋筒
铅锤
沙 堆
从圆锥的顶点到圆心的距离是圆锥的高
顶点
底面
高
侧面
练一练:下列哪个图形是圆锥?
异同点
主页
1、说一说圆锥有哪些特征?
(1)顶部:尖顶;
(2)底面:是一个圆;
(3)侧面:是一个曲面(展开是一个扇形);
(4)底面圆周上任一点与顶点之间的距离都相等。
(5)高只有一条。
想一想:
圆柱和圆锥的底和高有什么关系
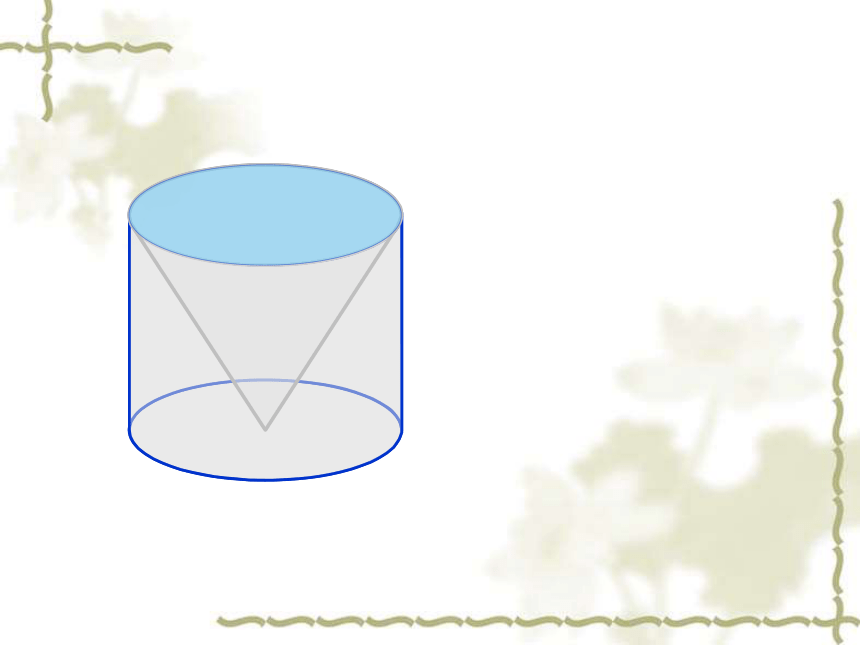
圆柱和圆锥等底等高
你发现了什么
圆柱的体积是与它等底等高圆锥体积的3倍.
圆柱体积=底面积 高
圆柱体积=底面积 高
圆柱体积=底面积 高
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
圆柱体积=底面积 高
圆锥体积=
底面积 高
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
实验报告表
实验器材
一桶水、等底等高
的圆柱和圆锥各一个
实验过程
①在空圆柱里满水倒入空圆锥里,( )次正好倒完。
在空圆锥里装 满水倒入空圆里,( )次正好装满。
结 论
②圆柱的体积是和它( )的圆锥体积的( )倍。
圆锥体积
计算公式
V=
②圆锥的体积是和它( )
的圆柱体积的
实 验 报 告 表
3
3
等底等高
等底等高
3
3
1
3
1
S h
主页
思考
思考
主页
要求圆锥的体积,必须知道
哪两个条件?为什么要乘
3
1
例1
例1 一个圆锥体,底面积是7.8平方分米,
高是1.8分米。这个圆锥的体积是多少
主页
V=1/3Sh
=1/3×7.8×1.8
=2.6×1.8
=4.68(平方分米)
答:这个圆锥的体积是4.68平方分米。
等底等高
1
24
×底面积×高
V= s h
一、填空:
1、圆锥的体积=( ),用字母表示是( )。
2、圆柱体积的 与和它( )的圆锥的体积相等。
3、一个圆柱和一个圆锥等底等高,圆柱的体积是3立方分米,圆锥的体积是( )立方分米。
4、一个圆锥的底面积是12平方厘米,高是6厘米,体积是( )立方厘米。
二、判断:
1、圆柱体的体积一定比圆锥体的体积大( )
2、圆锥的体积等于和它等底等高的圆柱体的 ( )
3、正方体、长方体、圆锥体的体积都等于底面积×高。 ( )
4、等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米。( )
√
×
√
×
即时训练
练一练 1、求下面各圆锥的体积。
(1)圆锥的底面积是0.9平方米,高是0.5米。 它的体积是多少立方米?
V=1/3Sh
=1/3×0.9×0.5
=0.3×0.5
=0.15(平方米)
答:它的体积是0.15平方米。
主页
如果已知圆锥的高和底面半径
(或直径、周长),怎样求圆锥的
体积呢?
想一想
主页
练习1
1、求下面各圆锥的体积。
(2)底面半径是2 厘米,高3厘米。
(3)底面直径是6分米,高6分米 。
巩 固 练 习
主页
1
2
3
练习2
巩 固 练 习
2、求下面各圆锥的体积。(单位:厘米)
(1) (2)
7 8 10
3
主页
1
2
3
练习3
思 考:
1、一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 18 立方米,
圆柱的体积是( )。
2、一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 12 厘米, 圆锥的
高是( )。
3、一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 314 平方米,
圆锥的底面积是( )。
主页
1
2
3
54 立方米
36 厘米
942 平方米
三:选择题
主页
1:一个圆柱的体积比与它等地等高圆锥体积多12立方厘米,这个圆锥体积是( )立方厘米。
A . 4 B.3 C. 6 D.9
2:一个圆锥和一个圆柱的相等,圆锥的底面半径是圆柱底面半径的2倍,那么圆锥体积是圆柱体积的( )
9倍
3倍
3
4
倍
A
B
C
C
A
