湖南省邵阳市新邵县2021年中考模拟数学试题(word版含答案)
文档属性
| 名称 | 湖南省邵阳市新邵县2021年中考模拟数学试题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 579.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 08:36:23 | ||
图片预览

文档简介
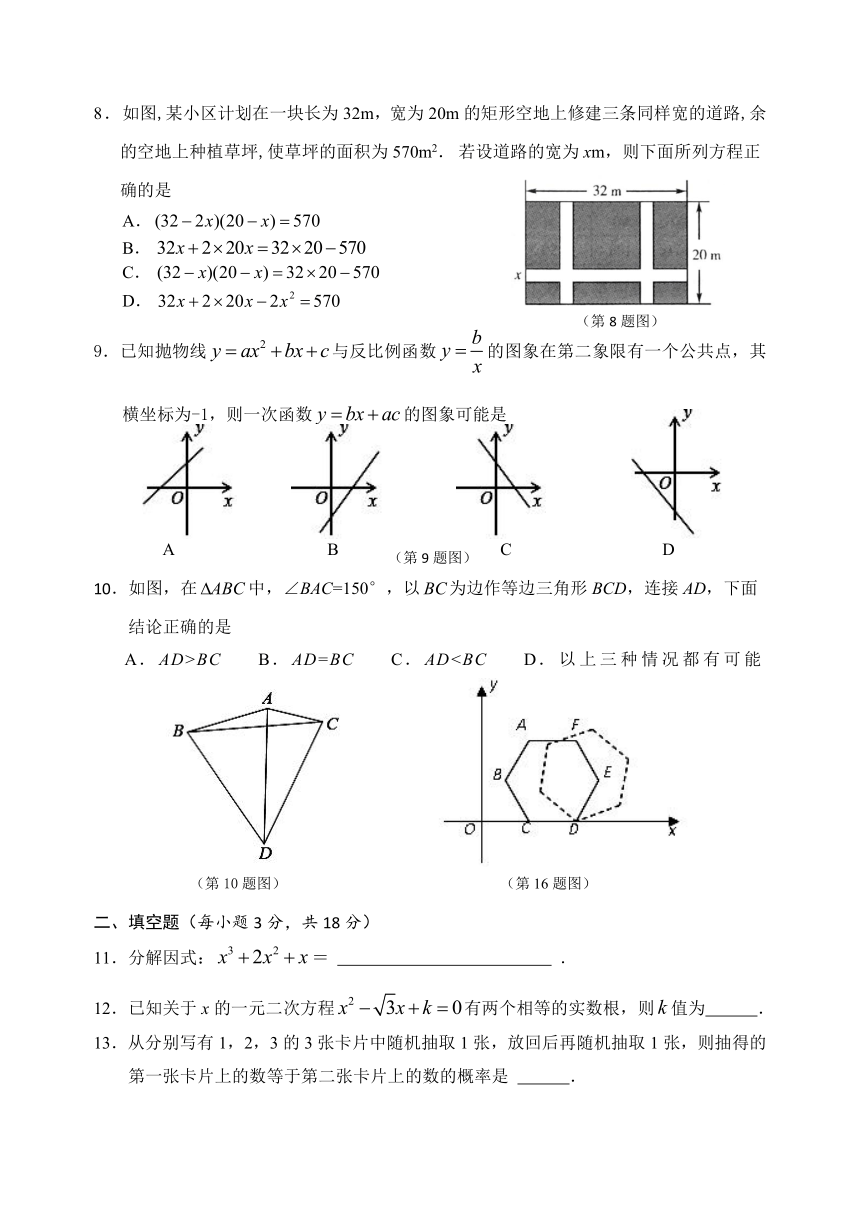
2021年中考摸拟试题
满分120分 考试时间150分钟
一、选择题(每小题3分,共30分)
1.
A. B. C. D.
2.纳米(nm)是非常小的长度单位,1 nm=m.新型冠状病毒的直径是100纳米,100纳米用科学记数法表示为
A.米 B.米 C.米 D.米
3.下面长方体的俯视图是
A B C D
4. 已知5位裁判员绐某运动员打出的分数为:88,91,89,90,91.则这组数据的中位数和平均数分别是
A.89和89.2 B.89和89.8 C.90和89.2 D.90和89.8
5.下列图形中,是轴对称图形但不是中心对称图形的是
A.等腰三角形 B.平行四边形 C.矩形 D.圆
6.如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线与直线b交于点C,若于AB=BC,∠1=50°,则∠2的度数为
(第6题图)
A.45° B.50° C.65° D.70°
7.不等式组的解集是
A. x<3 B. x≤-1 C. -1≤x<3 D. x<-1
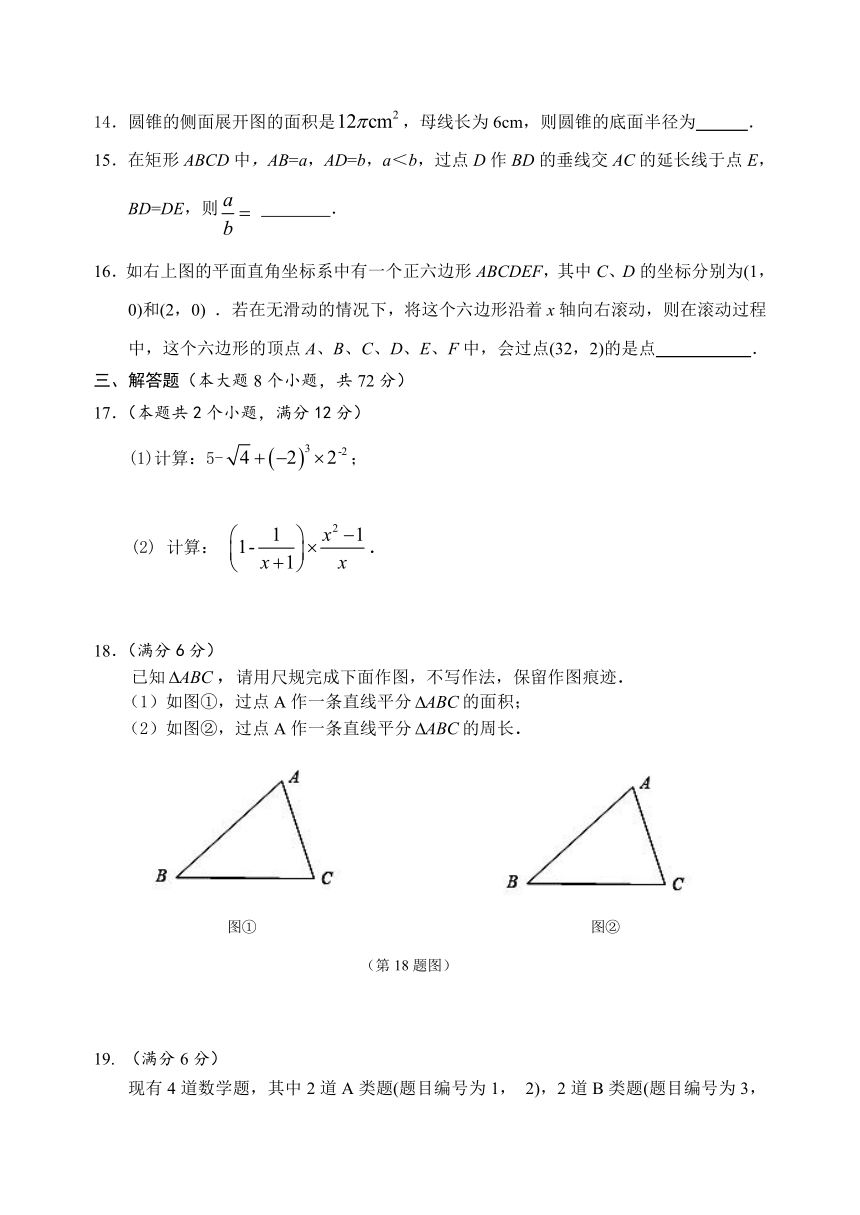
8.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是
A.
B.
C.
D.
9.已知抛物线与反比例函数的图象在第二象限有一个公共点,其横坐标为-1,则一次函数的图象可能是
A B C D
10.如图,在中,∠BAC=150°,以为边作等边三角形BCD,连接AD,下面结论正确的是
A.AD>BC B.AD=BC C.AD(第10题图) (第16题图)
二、填空题(每小题3分,共18分)
11.分解因式:= .
12.已知关于x的一元二次方程有两个相等的实数根,则值为 .
13.从分别写有1,2,3的3张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数等于第二张卡片上的数的概率是 .
14.圆锥的侧面展开图的面积是,母线长为6cm,则圆锥的底面半径为 .
15.在矩形ABCD中,AB=a,AD=b,a<b,过点D作BD的垂线交AC的延长线于点E,BD=DE,则 .
16.如右上图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0) .若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(32,2)的是点 .
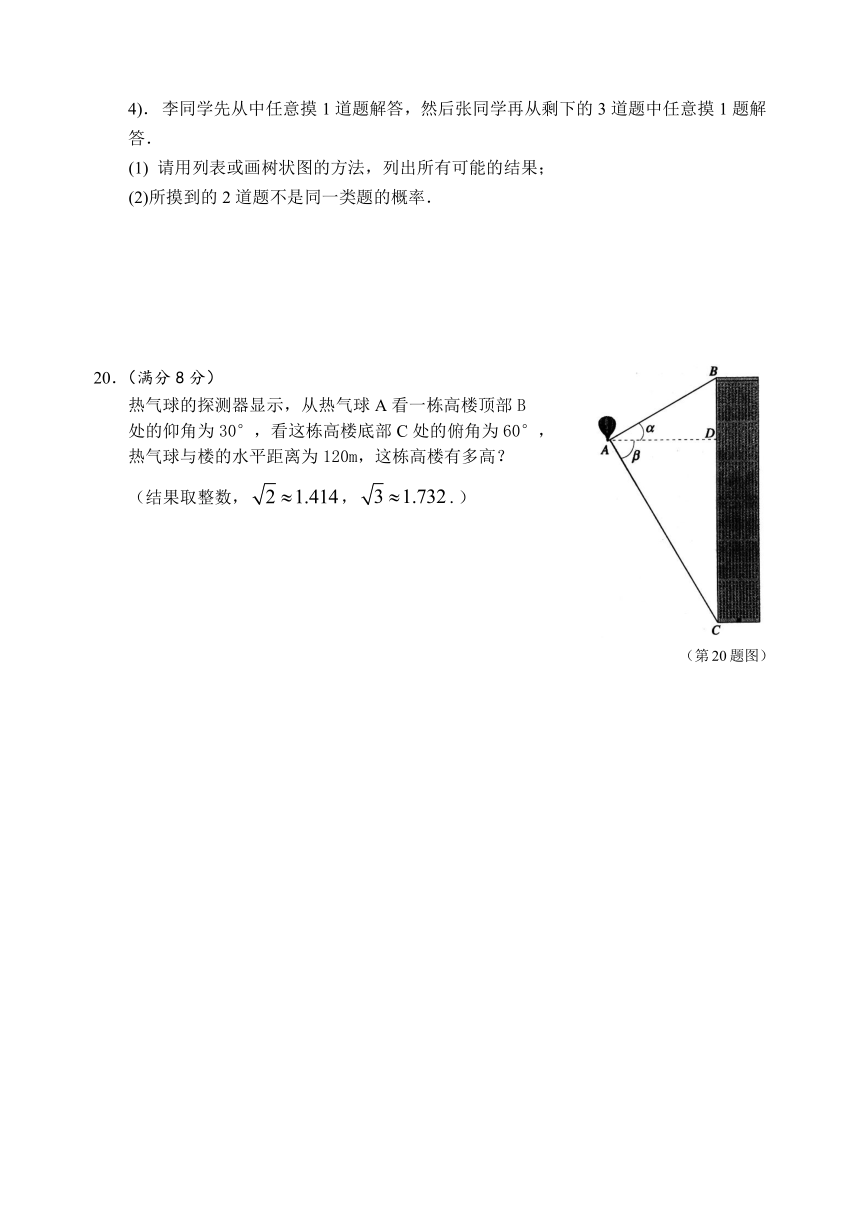
三、解答题(本大题8个小题,共72分)
17.(本题共2个小题,满分12分)
(1)计算:5-;
(2) 计算: .
18.(满分6分)
已知,请用尺规完成下面作图,不写作法,保留作图痕迹.
(1)如图①,过点A作一条直线平分的面积;
(2)如图②,过点A作一条直线平分的周长.
图① 图②
(第18题图)
19. (满分6分)
现有4道数学题,其中2道A类题(题目编号为1, 2),2道B类题(题目编号为3,4).李同学先从中任意摸1道题解答,然后张同学再从剩下的3道题中任意摸1题解答.
(1) 请用列表或画树状图的方法,列出所有可能的结果;
(2)所摸到的2道题不是同一类题的概率.
20.(满分8分)
热气球的探测器显示,从热气球A看一栋高楼顶部B
处的仰角为30°,看这栋高楼底部C处的俯角为60°,
热气球与楼的水平距离为120m,这栋高楼有多高?
(结果取整数,,.)
(第20题图)
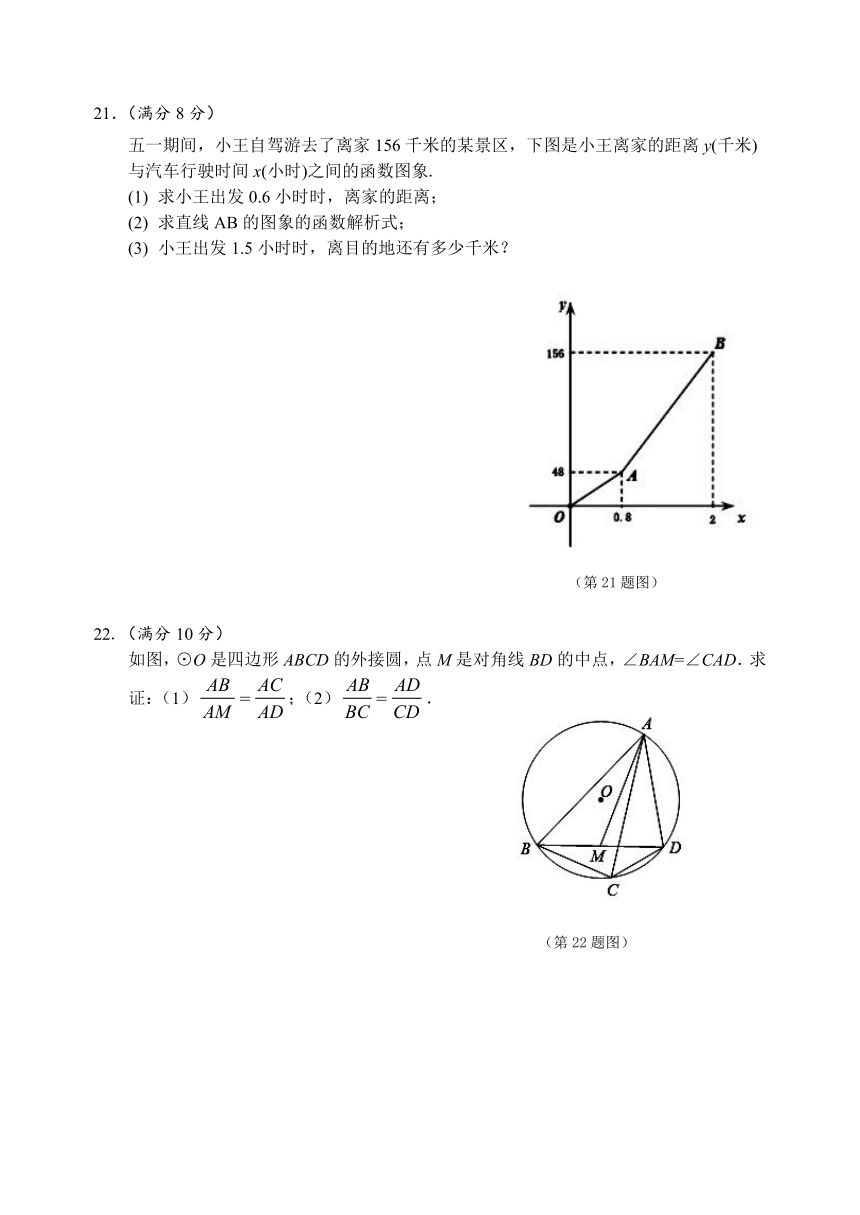
21.(满分8分)
五一期间,小王自驾游去了离家156千米的某景区,下图是小王离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
求小王出发0.6小时时,离家的距离;
求直线AB的图象的函数解析式;
小王出发1.5小时时,离目的地还有多少千米?
(第21题图)
22.(满分10分)
如图,⊙O是四边形ABCD的外接圆,点M是对角线BD的中点,∠BAM=∠CAD.求证:(1);(2).
(第22题图)
23.(满分10分)
如图①,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1) 请判断:FG与CE的数量关系是 ,位置关系是 ;
(2) 如图②,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中的结论是否仍然成立?请作出判断并给予证明;
(3) 如图③,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中的结论是否仍然成立?请直接写出你的判断.
图① 图② 图③
(第23题图)
24.(满分12分)
如图,在平面直角坐标系中,二次函数的图
象经过点、,与轴交于点,点在线
段上,,点在第二象限,
∠ADE=90°,tan∠DAE=,,垂足为.
(1)求这个二次函数的解析式;
(2)求线段、的长(用含的代数式表示);
(3)当∠ECA=∠OAC时,求的值.
(第24题图)
2021年中考摸拟试题答案
一、选择题(每小题3分,共30分)
1——5 BBDDA 6——10 CBADB
二、填空题(每小题3分,共18分)
11.x (x+1) 2; 12. ; 13. ; 14.2cm; 15. ; 16. A.
三、解答题(共72分)
17. 解:(1)原式5-2+(-8)×
3-2
1.
(2)原式
=x-1
18. 说明:(1)如图①,作BC的垂直平分线交BC于点D,再过A、D两点作直线AD,直线AD为所求作的直线;
(2)如图②,延长CB至E使BE=AB,延长BC至F使CF=AC,作EF的垂直平分线交BC于点D,再过A、D两点作直线AD,直线AD为所求作的直线.
图① 图②
19. 解:(1)画树状图如下:
共有12种等可能的结果;
(2)所摸到的2道题不是同一类题的结果数为8,
所摸到的2道题不是同一类题的概率为:.
20. 解:由第20题图知:,,AD=120.
∵,,
∴ ,
.
∴.
因此, 这栋楼高约为277m.
21. 解:(1)由图象可设OA段图象的解析式为:,
当x为0.8时,y=48,∴k=60,().
当x为0.6时,y=60×0.6=36.
答:小王出发0.6小时时,离家的距离是36千米;
(2)由图象可设AB图象的解析式为:,
因为点A(0.8,48),B(2,156)在直线AB上,得
,解得:.
直线AB的图象的函数解析式为:;
(3)当x为1.5时,y=90×1.5-24=111,
∴156-111=45.
答:小王出发1.5小时时,离目的地还有45千米.
22. 证:(1)∵,
∴,
即.
又,
∴∽.
∴.
(2)由∽得:
.
∵, ,
∴∽.
∴.
又,
∴ .
23. 解:(1)FG=CE, FG∥CE;
(2)(1)中的结论仍然成立.
∵四边形ABCD为正方形,
∴BCCD,∠FBC ∠ECD90°.
在△FBC与△ECD中,
∴△FBC≌△ECD(SAS) .
∴FC=DE,∠1=∠EDC.
∵EG=DE,
∴FC=EG.
∵∠1+∠2=90°,
∴∠EDC+∠2=90°.
∴∠3=∠EDC+∠2=90°.
∵EG⊥DE,
∴∠4=90°.
∴∠3=∠4.
∴FC∥EG.
∴四边形GECF为平行四边形.
∴FG=CE, FG∥CE.
(3)成立.
24. 解:(1)二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),
∴,解得.
∴这个二次函数的解析式为:y=﹣2x2+6x+8.
(2) ∵∠EFD=∠EDA=90°,∴∠DEF+∠EDF=90°,∠EDF+∠ODA=90°.
∴∠DEF=∠ODA.∴△EDF∽△DAO.∴.
∵,∴.
∵OD=t,∴,∴EF=.
同理,
∴DF=2,∴OF=t﹣2.
(3)∵抛物线的解析式为:y=﹣2x2+6x+8,∴C(0,8),OC=8.
如图,连接EC、AC,过A作EC的垂线交EC于G点.
在△ACG与△CAO中,
∵∠OAC=∠GCA,AC=CA,∠CGA=∠AOC,
∴△ACG≌△CAO(AAS).
∴CG=AO=4,AG=OC=8.
如图,过E点作EM⊥x轴于点M,
则在Rt△AEM中,EM=OF=t﹣2,AM=OA+OM=OA+EF=4+,
由勾股定理得: .
在Rt△AEG中,由勾股定理得:
.
在Rt△ECF中,EF=,CF=OC﹣OF=10﹣t,CE=CG+EG=4+.
由勾股定理得:EF2+CF2=CE2,
即.
解得t1=10(不合题意,舍去),t2=6.
∴t=6.
(第8题图)
(第9题图)
PAGE
满分120分 考试时间150分钟
一、选择题(每小题3分,共30分)
1.
A. B. C. D.
2.纳米(nm)是非常小的长度单位,1 nm=m.新型冠状病毒的直径是100纳米,100纳米用科学记数法表示为
A.米 B.米 C.米 D.米
3.下面长方体的俯视图是
A B C D
4. 已知5位裁判员绐某运动员打出的分数为:88,91,89,90,91.则这组数据的中位数和平均数分别是
A.89和89.2 B.89和89.8 C.90和89.2 D.90和89.8
5.下列图形中,是轴对称图形但不是中心对称图形的是
A.等腰三角形 B.平行四边形 C.矩形 D.圆
6.如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线与直线b交于点C,若于AB=BC,∠1=50°,则∠2的度数为
(第6题图)
A.45° B.50° C.65° D.70°
7.不等式组的解集是
A. x<3 B. x≤-1 C. -1≤x<3 D. x<-1
8.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是
A.
B.
C.
D.
9.已知抛物线与反比例函数的图象在第二象限有一个公共点,其横坐标为-1,则一次函数的图象可能是
A B C D
10.如图,在中,∠BAC=150°,以为边作等边三角形BCD,连接AD,下面结论正确的是
A.AD>BC B.AD=BC C.AD
二、填空题(每小题3分,共18分)
11.分解因式:= .
12.已知关于x的一元二次方程有两个相等的实数根,则值为 .
13.从分别写有1,2,3的3张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数等于第二张卡片上的数的概率是 .
14.圆锥的侧面展开图的面积是,母线长为6cm,则圆锥的底面半径为 .
15.在矩形ABCD中,AB=a,AD=b,a<b,过点D作BD的垂线交AC的延长线于点E,BD=DE,则 .
16.如右上图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0) .若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(32,2)的是点 .
三、解答题(本大题8个小题,共72分)
17.(本题共2个小题,满分12分)
(1)计算:5-;
(2) 计算: .
18.(满分6分)
已知,请用尺规完成下面作图,不写作法,保留作图痕迹.
(1)如图①,过点A作一条直线平分的面积;
(2)如图②,过点A作一条直线平分的周长.
图① 图②
(第18题图)
19. (满分6分)
现有4道数学题,其中2道A类题(题目编号为1, 2),2道B类题(题目编号为3,4).李同学先从中任意摸1道题解答,然后张同学再从剩下的3道题中任意摸1题解答.
(1) 请用列表或画树状图的方法,列出所有可能的结果;
(2)所摸到的2道题不是同一类题的概率.
20.(满分8分)
热气球的探测器显示,从热气球A看一栋高楼顶部B
处的仰角为30°,看这栋高楼底部C处的俯角为60°,
热气球与楼的水平距离为120m,这栋高楼有多高?
(结果取整数,,.)
(第20题图)
21.(满分8分)
五一期间,小王自驾游去了离家156千米的某景区,下图是小王离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
求小王出发0.6小时时,离家的距离;
求直线AB的图象的函数解析式;
小王出发1.5小时时,离目的地还有多少千米?
(第21题图)
22.(满分10分)
如图,⊙O是四边形ABCD的外接圆,点M是对角线BD的中点,∠BAM=∠CAD.求证:(1);(2).
(第22题图)
23.(满分10分)
如图①,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1) 请判断:FG与CE的数量关系是 ,位置关系是 ;
(2) 如图②,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中的结论是否仍然成立?请作出判断并给予证明;
(3) 如图③,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中的结论是否仍然成立?请直接写出你的判断.
图① 图② 图③
(第23题图)
24.(满分12分)
如图,在平面直角坐标系中,二次函数的图
象经过点、,与轴交于点,点在线
段上,,点在第二象限,
∠ADE=90°,tan∠DAE=,,垂足为.
(1)求这个二次函数的解析式;
(2)求线段、的长(用含的代数式表示);
(3)当∠ECA=∠OAC时,求的值.
(第24题图)
2021年中考摸拟试题答案
一、选择题(每小题3分,共30分)
1——5 BBDDA 6——10 CBADB
二、填空题(每小题3分,共18分)
11.x (x+1) 2; 12. ; 13. ; 14.2cm; 15. ; 16. A.
三、解答题(共72分)
17. 解:(1)原式5-2+(-8)×
3-2
1.
(2)原式
=x-1
18. 说明:(1)如图①,作BC的垂直平分线交BC于点D,再过A、D两点作直线AD,直线AD为所求作的直线;
(2)如图②,延长CB至E使BE=AB,延长BC至F使CF=AC,作EF的垂直平分线交BC于点D,再过A、D两点作直线AD,直线AD为所求作的直线.
图① 图②
19. 解:(1)画树状图如下:
共有12种等可能的结果;
(2)所摸到的2道题不是同一类题的结果数为8,
所摸到的2道题不是同一类题的概率为:.
20. 解:由第20题图知:,,AD=120.
∵,,
∴ ,
.
∴.
因此, 这栋楼高约为277m.
21. 解:(1)由图象可设OA段图象的解析式为:,
当x为0.8时,y=48,∴k=60,().
当x为0.6时,y=60×0.6=36.
答:小王出发0.6小时时,离家的距离是36千米;
(2)由图象可设AB图象的解析式为:,
因为点A(0.8,48),B(2,156)在直线AB上,得
,解得:.
直线AB的图象的函数解析式为:;
(3)当x为1.5时,y=90×1.5-24=111,
∴156-111=45.
答:小王出发1.5小时时,离目的地还有45千米.
22. 证:(1)∵,
∴,
即.
又,
∴∽.
∴.
(2)由∽得:
.
∵, ,
∴∽.
∴.
又,
∴ .
23. 解:(1)FG=CE, FG∥CE;
(2)(1)中的结论仍然成立.
∵四边形ABCD为正方形,
∴BCCD,∠FBC ∠ECD90°.
在△FBC与△ECD中,
∴△FBC≌△ECD(SAS) .
∴FC=DE,∠1=∠EDC.
∵EG=DE,
∴FC=EG.
∵∠1+∠2=90°,
∴∠EDC+∠2=90°.
∴∠3=∠EDC+∠2=90°.
∵EG⊥DE,
∴∠4=90°.
∴∠3=∠4.
∴FC∥EG.
∴四边形GECF为平行四边形.
∴FG=CE, FG∥CE.
(3)成立.
24. 解:(1)二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),
∴,解得.
∴这个二次函数的解析式为:y=﹣2x2+6x+8.
(2) ∵∠EFD=∠EDA=90°,∴∠DEF+∠EDF=90°,∠EDF+∠ODA=90°.
∴∠DEF=∠ODA.∴△EDF∽△DAO.∴.
∵,∴.
∵OD=t,∴,∴EF=.
同理,
∴DF=2,∴OF=t﹣2.
(3)∵抛物线的解析式为:y=﹣2x2+6x+8,∴C(0,8),OC=8.
如图,连接EC、AC,过A作EC的垂线交EC于G点.
在△ACG与△CAO中,
∵∠OAC=∠GCA,AC=CA,∠CGA=∠AOC,
∴△ACG≌△CAO(AAS).
∴CG=AO=4,AG=OC=8.
如图,过E点作EM⊥x轴于点M,
则在Rt△AEM中,EM=OF=t﹣2,AM=OA+OM=OA+EF=4+,
由勾股定理得: .
在Rt△AEG中,由勾股定理得:
.
在Rt△ECF中,EF=,CF=OC﹣OF=10﹣t,CE=CG+EG=4+.
由勾股定理得:EF2+CF2=CE2,
即.
解得t1=10(不合题意,舍去),t2=6.
∴t=6.
(第8题图)
(第9题图)
PAGE
同课章节目录
