2021-2022学年北师大版九年级数学下册1.6利用三角函数测高 同步达标训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.6利用三角函数测高 同步达标训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 545.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 17:55:04 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《1.6利用三角函数测高》同步达标训练(附答案)
1.重庆实验外国语学校坐落在美丽且有灵气的华岩寺旁边,特别是金灿灿的大佛让身高1.6米的小王同学很感兴趣,刚刚学过三角函数知识,他就想测一下大佛的高度,小王到A点测得佛顶仰角为37°,接着向大佛走了10米来到B处,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C处,此时与大佛的水平距离DH=6.2米(其中点A、B、C、E、F在同一平面内,点A、B、F在同一条直线上),请问大佛的高度EF为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80).
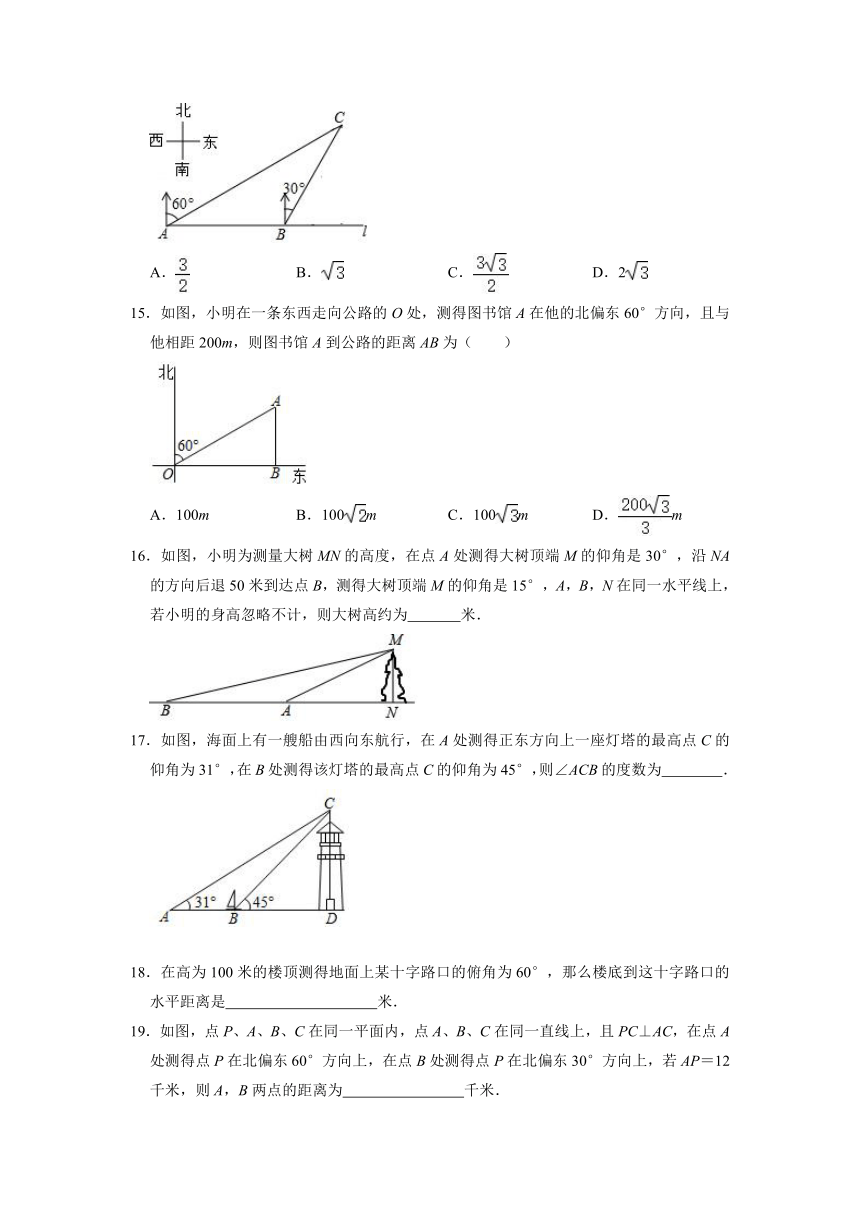
A.15米 B.16米 C.17米 D.18米
2.如图,小明为了测量照母山上“览星塔”AB的高度,先从与塔底中心B在同一水平面上的点D出发,沿着坡度为1:0.75的斜坡DE行走10米至坡顶E处,再从E处沿水平方向继续前行若干米后至点F处,在F点测得塔顶A的仰角为63°,塔底C的俯角为45°,B与C的水平距离为4米(图中A、B、C、D、E、F在同一平面内,E、F和D、C、B分别在同一水平线上),根据小明的测量数据,计算出“览星塔”AB的高度约为(计算结果精确到0.1米,参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)( )
A.17.8米 B.23.7米 C.31.5米 D.37.4米
3.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
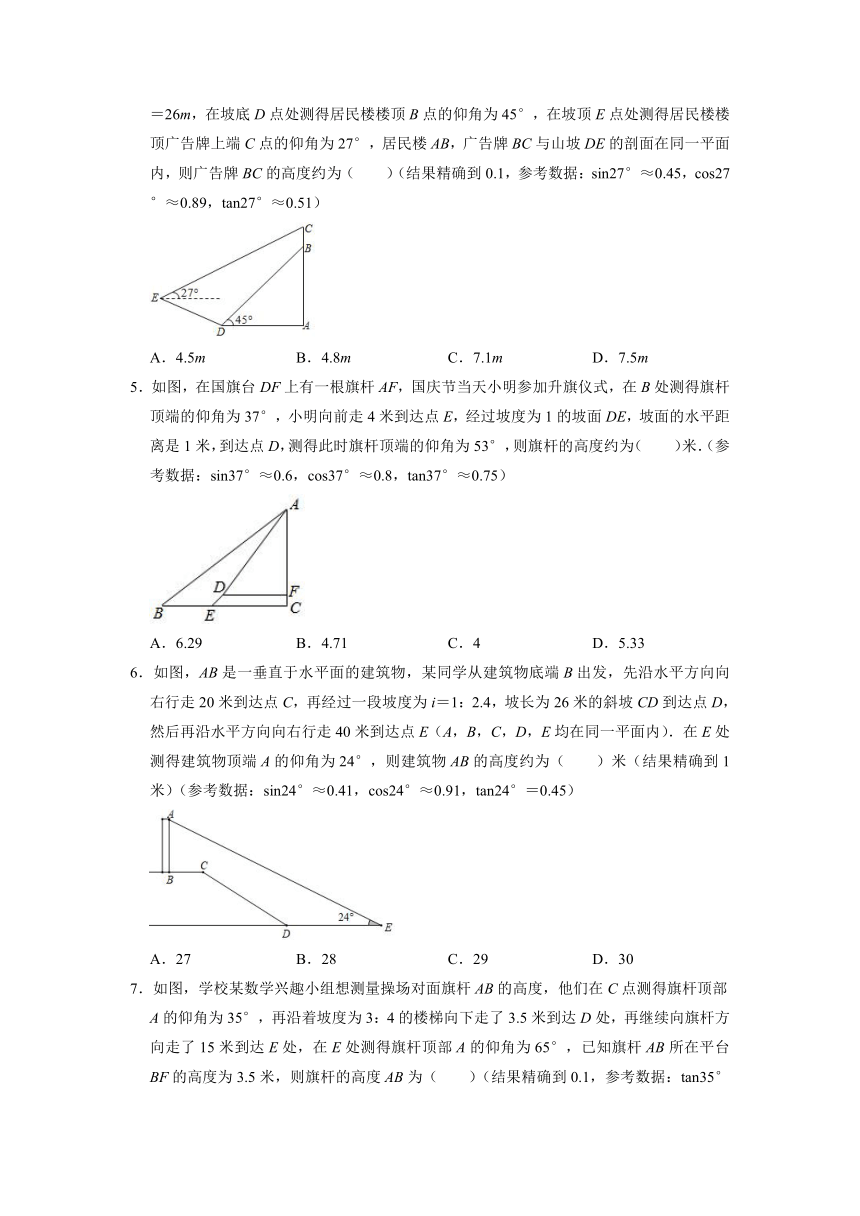
4.如图,在某居民楼AB楼顶有一广告牌BC,在距楼底A点左侧水平距离30m的D点处有一个山坡,山坡DE的坡度(或坡比)i=1:2.4,山坡坡底D点到坡顶E点的距离DE=26m,在坡底D点处测得居民楼楼顶B点的仰角为45°,在坡顶E点处测得居民楼楼顶广告牌上端C点的仰角为27°,居民楼AB,广告牌BC与山坡DE的剖面在同一平面内,则广告牌BC的高度约为( )(结果精确到0.1,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.4.5m B.4.8m C.7.1m D.7.5m
5.如图,在国旗台DF上有一根旗杆AF,国庆节当天小明参加升旗仪式,在B处测得旗杆顶端的仰角为37°,小明向前走4米到达点E,经过坡度为1的坡面DE,坡面的水平距离是1米,到达点D,测得此时旗杆顶端的仰角为53°,则旗杆的高度约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6.29 B.4.71 C.4 D.5.33
6.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度为i=1:2.4,坡长为26米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为( )米(结果精确到1米)(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)
A.27 B.28 C.29 D.30
7.如图,学校某数学兴趣小组想测量操场对面旗杆AB的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,已知旗杆AB所在平台BF的高度为3.5米,则旗杆的高度AB为( )(结果精确到0.1,参考数据:tan35°≈0.7,tan65°≈2.1).
A.19.8米 B.19.7米 C.18.3米 D.16.2米
8.如图,小明站在距一棵树(CD)20m的点B处,小明的眼睛(点A)与地面的距离为1.6m,测得树梢(点C)的仰角为28°,那么这棵树的高度为( )
A.20tan28°m B.20sin28°m
C.(20tan28°+1.6)m D.(20sin28°+1.6)m
9.如图,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28km/时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,此时,灯塔M与渔船的距离是( )
A.7km B.14km C.7km D.14km
10.如图,大楼高30m,远处有一塔BC,某人爬到楼顶D测得塔顶的仰角为30°,且测得D、B相距30m,则塔高BC为( )m.
A.40 B.45 C.30+ D.30
11.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
12.在数学综合实践课上,老师和同学们一起测量学校旗杆的高度,他们首先在旗杆底部C地测得旗杆顶部A的仰角为45°,然后沿着斜坡CD到斜坡顶部D点处再测得旗杆顶部A的仰角为37°(身高忽略不计),已知斜坡CD的坡度i=1:2.4,坡面CD长2.6米,旗杆AB所在旗台高度为1.4米,旗杆、旗台底部、斜坡在同一平面,则旗杆AB的高度为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.9.5米 B.9.6米 C.9.7米 D.9.8米
13.如图,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距( )
A.m(cosα+sinα)米 B.m(cosα﹣sinα)米
C.米 D.米
14.如图,在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )km.
A. B. C. D.2
15.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )
A.100m B.100m C.100m D.m
16.如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为 米.
17.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为 .
18.在高为100米的楼顶测得地面上某十字路口的俯角为60°,那么楼底到这十字路口的水平距离是 米.
19.如图,点P、A、B、C在同一平面内,点A、B、C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 千米.
20.如图,为了测量塔CD的高度,小明在A处仰望塔顶,测得仰角为30°,再往塔的方向前进60m至B处,测得仰角为60°,那么塔的高度是 m.(小明的身高忽略不计,结果保留根号).
21.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为 m.(结果保留根号)
22.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC= 米(结果保留根号).
23.在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距 千米.(结果精确到0.1千米,参考数据:≈1.414,≈1.732)
24.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为 海里.
25.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为 .(参考数据:tan37°≈,tan53°≈)
26.如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球“的宣传牌,已知立杆AB的高度是4m,从地面上某处D点测得宣传牌顶端C和底端B点的仰角分别是62°和45°、求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
27.如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=50m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,求居民楼AB的高度.(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
28.为了测量建筑物的高度AB,兴趣小组在C处用高为1.5米的测角仪CD,测得屋顶B的仰角为45°,再向房屋方向前进15米,又测得房屋的顶端B的仰角为61°,求房屋的高度AB.(参考数据sin61°≈0.87,tan61°≈1.80,结果保留整数)
29.如图,一艘渔船沿南偏东42°方向航行,在A处测得一个小岛P在其南偏东64°方向.又继续航行(40﹣16)海里到达B处,测得小岛P位于渔船的南偏东72°方向,已知以小岛P为圆心,半径16海里的圆形海域内有暗礁.如果渔船不改变航向有没有触礁的危险,请通过计算加以说明.如果有危险,渔船自B处开始,沿南偏东多少度的方向航行,能够安全通过这一海域?(参考数据:sin22°=,cos22°=,tan22°=)
30.如图,052D型驱逐舰“昆明舰”执行任务后正返回葫芦岛军港C,途经渤海海域A处时,葫芦岛军港C的中国海军发现点A在南偏东30°方向上,旅顺军港B的中国海军发现点A在正西方向上.已知军港C在军港B的北偏西60°方向,且B、C两地相距120海里.(计算结果保留根号)
(1)求出此时点A到军港C的距离;
(2)若“昆明舰”从A处沿AC方向向军港C驶去,当到达点A′时,测得军港B在A′的南偏东75°的方向上,求此时“昆明舰”的航行距离.
参考答案
1.解:过点C作CM⊥BF于点M,过点G作GN⊥EF于点N,
∵斜坡BC的坡度i=4:3,BC=5米,
∴设CM=4x,BM=3x,
∴(4x)2+(3x)2=52,
解得x=1,
∴CM=4米,BM=3米,
由题意可知四边形DHFM和四边形AGNF是矩形,
∴DH=FM=6.2米,
∵AB=10米,
∴AF=GN=AB+BM+MF=10+3+6.2=19.2米,
在Rt△ENG中,∵∠EGN=37°,
∴tan37°=≈0.75,
∴EN=0.75×NG=0.75×19.2=14.4米,
∴EF=EN+NF=14.4+1.6=16米.
故选:B.
2.解:过F作FG⊥AB于G,过C作CH⊥FG于H,如图所示:
则PE=CH=BG,GH=BC=4,
∵斜坡DE的坡度为1:0.75,
∴==,
设PD=3x,则PE=4x,
在Rt△PDE中,由勾股定理得:DE==5x,
∴5x=10,
∴x=2,
∴CH=BG=PE=8,
∵∠CFH=45°,
∴△CFH是等腰直角三角形,
∴FH=CH=8,
∴FG=FH+GH=12,
在Rt△AFG中,tan∠AFG=,
∴AG=FG×tan63°≈12×1.96=23.52,
∴AB=AG+BG=23.52+8=31.5(米),
即“览星塔”AB的高度约为31.5米,
故选:C.
3.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC tanα=2tanα,
故选:B.
4.解:作EF⊥AB于F,作DG⊥EF于G,如图所示:
则GF=AD=30m,AF=DG,∠CEF=27°,
∵山坡DE的坡度i==,
∴EG=2.4DG,
∵DE=26m,DE2+EG2=DE2,
∴AF=DG=10m,EG=24m,
∴EF=EG+GF=54m,
在Rt△CEF中,tan∠CEF==tan27°≈0.51,
∴CF≈0.51×54=27.54(m),
∴AC=AF+CF=10+27.54=37.54(m),
又∵∠ADB=45°,∠A=90°,
∴△ABD是等腰直角三角形,
∴AB=AD=30m,
∴BC=AC﹣AB=37.54﹣30≈7.5(m);
故选:D.
5.解:过点D作DM⊥BC,垂足为M,由题意得,
∠B=37°,∠ADF=53°,BE=4,EM=1,
∵坡面DE的坡度为1,
∴=1,
∴DM=EM=1=FC,
在Rt△ADF中,∠DAF=90°﹣∠ADF=90°﹣53°=37°,
∵tan∠DAF=≈0.75,
设AF=x,则DF=0.75x=MC,
在Rt△ABC中,
∵tan∠B=,
∴tan37°=≈0.75,
解得x=≈6.29(米),
故选:A.
6.解:如图,延长AB交ED的延长线于F,作CG⊥EF于G,
由题意得:FG=BC=20米,DE=40米,BF=CG,
在Rt△CDG中,i=1:2.4,CD=26米,
∴BF=CG=10米,GD=24米,
在Rt△AFE中,∠AFE=90°,FE=FG+GD+DE=84米,∠E=24°,
∴AF=FE tan24°≈84×0.45=37.8(米),
∴AB=AF﹣BF=37.8﹣10≈28(米);
即建筑物AB的高度为28米;
故选:B.
7.解:作CG⊥AF于G,DH⊥CG于H,如图所示:
则HG=DF,FG=DH,
∵楼梯CD的坡度为3:4,CD=3.5,
∴FG=DH=2.1,CH=2.8,
在Rt△ACG中,∠ACG=35°,tan∠ACG==tan35°≈0.7,
∴AG≈0.7CG,
∴AF=AG+FG=0.7CG+2.1,
∵DF=HG=CG﹣CH=CG﹣2.8,
∴EF=DF﹣DE=CG﹣2.8﹣15=CG﹣17.8,
在Rt△AEF中,∠AEF=65°,tan∠AEF==tan65°≈2.1,
∴AF=2.1EF,
∴0.7CG+2.1=2.1(CG﹣17.8),
解得:CG=28.2,
∴AF=0.7×28.2+2.1=21.84,
∴AB=AF﹣BF=21.84﹣3.5≈18.3(米),
即旗杆的高度AB约为18.3米;
故选:C.
8.解:作AE⊥CD于E,如图所示:
则ED=AB=1.6m,AE=BD=20m,
在Rt△ACE中,∠CAE=28°,
∵tan∠CAE=,
∴CE=AE×tan∠CAE=20tan28°,
∴CD=CE+ED=(20tan28°+1.6)m;
故选:C.
9.解:如图,过点M作MC⊥AB于点C,过点B作BN⊥AM于点N,
由题意得,∠MAB=30°,∠MBC=75°,
∵∠CBM=∠BAM+∠AMB,
∴∠AMB=∠NAM=45°,
∴BN=MN,
∵AB=28×0.5=14km,
∴BN==7km,
∴BM=NB=7(km).
故选:A.
10.解:过点D作DE⊥BC于点E,
∵∠BDE=30°,BD=30m,
∴BE=BD=15m,
∵AD=30m,
∴CE=30m,
∴BC=CE+BE=30+15=45m.
故选:B.
11.解:如图,过点D作DE⊥AC于点E,DF⊥AB于点F,
根据题意可知:
BA⊥AC,
∴四边形FAED是矩形,
∴FA=DE,DF=AE,
∵斜坡CD的长为6m,坡度i=DE:CE=1:0.75,
∴DE=4.8,CE=3.6,
∴DF=AE=AC+CE=11.6,
在Rt△BFD中,∠BDF=46°,
∴BF=DF tan46°≈11.6×1.04≈12.064,
∴BA=BF+FA=12.064+4.8≈16.9(m).
所以教学楼的高度约为16.9米.
故选:C.
12.解:作DH⊥FC交FC的延长线于点H,延长AB交CF的延长线于点T,作DJ⊥AT于点J,如图所示:
则四边形EFTB与四边形DHTJ都是矩形,
∴BT=EF=1.4米,JT=DH,
在Rt△DCH中,CD=2.6米,=,
∴DH=1(米),CH=2.4(米),
∵∠ACT=45°,∠T=90°,
∴AT=TC,
设AT=TC=x.则DJ=TH=(x+2.4)米,AJ=(x﹣1)米,
在Rt△ADJ中,tan∠ADJ==0.75,
∴=0.75,
解得:x=11.2,
∴AB=AT﹣BT=11.2﹣1.4=9.8(米),
故选:D.
13.解:过点C作CD⊥AB于D,如图所示:
由题意得:∠ACD=45°,∠DCB=α,
在Rt△BCD中,BC=m,
∴DB=BCsinα°=m sinα(米),CD=BCcosα=m cosα(米),
在Rt△ACD中,AD=CD=m cosα(米),
∴AB=AD+DB=m(cosα+sinα)(米).
故选:A.
14.解:过点C作CD⊥AB于点D,
根据题意得:∠CAD=90°﹣60°=30°,
∠CBD=90°﹣30°=60°,
∴∠ACB=∠CBD﹣∠CAD=30°,
∴∠CAB=∠ACB,
∴BC=AB=3km,
在Rt△CBD中,
∴CD=BC sin60°=3×(km).
∴船C到海岸线l的距离是km.
故选:C.
15.解:由题意得,∠AOB=90°﹣60°=30°,
∴AB=OA=100(m),
故选:A.
16.解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=AM=25米;
故答案为:25.
17.解:由题意得:∠BAC=31°,∠CBD=45°,
∵∠CBD=∠BAC+∠ACB,
∴∠ACB=∠CBD﹣∠BAC=45°﹣31°=14°,
故答案为:14°.
18.解:如图所示:
由题意得:∠B=90°,∠BAC=60°,BC=100米,
∵tan∠BAC=,
∴AB===(米),
即楼底到这十字路口的水平距离是米,
故答案为:.
19.解:∵PC⊥AC,在点A处测得点P在北偏东60°方向上,
∴∠PCA=90°,∠PAC=30°,
∵AP=12千米,
∴PC=6千米,AC=6千米,
∵在点B处测得点P在北偏东30°方向上,∠PCB=90°,PC=6千米,
∴∠PBC=60°,
∴BC===2千米,
∴AB=AC﹣BC=6﹣2=4(千米),
故答案为:4千米.
20.解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=60m.
∴DC=BD sin60°=60×=30(m),
答:该塔高为30m,
故答案为:30.
21.解:∵在Rt△ABD中,AD=90,∠BAD=45°,
∴BD=AD=30(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD tan60°=30×=30(m),
∴BC=BD+CD=30+30(m)
答:该建筑物的高度BC约为(30+30)米.
故答案为:(30+30).
22.解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米);
故答案为:(100+100).
23.解:∵B在A的正东方,C在A地的北偏东 60°方向,
∴∠BAC=90°﹣60°=30°,
∵C在B地的北偏东15°方向,
∴∠ABC=90°+15°=105°,
∴∠C=180°﹣∠BAC﹣∠ABC=180°﹣30°﹣105°=45°,
过B作BD⊥AC于D,
在Rt△ABD中,∠BAD=30°,AB=4km,
∴BD=AB=2km,AD=2km,
在Rt△BCD中,∠C=45°,
∴CD=BD=2km,
∴AC=AD+CD=(2+2)≈5.5km,
答:A、C两地相距5.5千米,
故答案为:5.5.
24.解:根据题意得:∠BAC=90°,AB=12海里,AC=9海里,
在Rt△ABC中,BC==15海里,
故答案为:15.
25.解:如图,作CE⊥BA于E.设EC=xm,BE=ym.
在Rt△ECB中,tan53°=,即,
在Rt△AEC中,tan37°=,即,
解得x=180,y=135,
∴AC===300(m),
故答案为:300m.
26.解:在Rt△ADB中,
∵∠BDA=45°,
∴AD=AB=4m.
在Rt△ADC中,AC=AD tan62°≈4×1.88=7.52(m).
∴BC=AC﹣AB=7.52﹣4=3.52≈3.5(m).
答:宣传牌BC的高度是3.5m.
27.解:如图,过点D作DF⊥AB,垂足为F,作DE⊥BC交BC的延长线于点E,
由题意得,∠ADF=28°,CD=50m,BC=60m,
在Rt△DEC中,
∵山坡CD的坡度i=1:0.75,
∴==,
设DE=4xm,则EC=3xm,由勾股定理可得CD=5xm,
又CD=50m,即5x=50,
∴x=10(m),
∴EC=3x=30(m),DE=4x=40(m)=FB,
∴BE=BC+EC=60+30=90(m)=DF,
在Rt△ADF中,
AF=tan28°×DF≈0.53×90≈47.7(m),
∴AB=AF+FB=47.7+40≈87.7(m),
即居民楼AB的高度约为87.7m.
28.解:由题意得,四边形DCEF,四边形MAEF都是矩形,
所以,AM=EF=CD=1.5米,DF=CE=15米,
设BM=x米,
在Rt△BMF中,
tan∠BFM=tan61°=≈1.80,
∴FM=,
在Rt△BDM中,
tan∠BDM=tan45°==1,
∴DM=BM=x,
∵DM=DF+FM,
∴x=15+,
解得,x=33.75,
∴AB=AM+BM=1.5+33.75≈35(米),
答:房屋的高度AB约为35米.
29.解:如图1,过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=64°﹣42°=22°,∠PBC=72°﹣42°=30°,AB=40﹣16,
设PC=x,
在Rt△PBC中,
∵∠PBC=30°,
∴BC=PC=x,
∴AC=AB+BC=40﹣16+x,
在Rt△PAC中,
∵∠PAC=22°,
∴tan∠PAC=,即=,
解得,x=16,即PC=16,BP=2PC=32,
∵16<16,
∴有危险.
如图2,渔船沿着BD方向航行,过点P作PD⊥BD,垂足为D,
在Rt△PBD中,
∵sin∠PBD===,
∴∠PBD=45°,
∴∠QBD=∠QBP﹣∠DBP=72°﹣45°=27°,
即渔船自B处开始,沿南偏东27°的方向航行,能够安全通过这一海域.
30.解:(1)如图所示:延长BA,过点C作CD⊥BA延长线与点D,
由题意可得:∠CBD=30°,BC=120海里,
则CD=BC=60海里,
∵cos∠ACD==cos30°=,
即=
∴AC=40(海里),
即此时点A到军港C的距离为40海里;
(2)过点A′作A′N⊥BC于点N,如图:
由(1)得:CD=60海里,AC=40海里,
∵A'E∥CD,
∴∠AA'E=∠ACD=30°,
∴∠BA′A=45°,
∵∠BA'E=75°,
∴∠ABA'=15°,
∴∠2=15°=∠ABA',
即A′B平分∠CBA,
∴A'E=A'N,
设AA′=x,则AE=AA',A'N=A′E=AE=x,
∵∠1=60°﹣30°=30°,A'N⊥BC,
∴A'C=2A'N=x,
∵A'C+AA'=AC,
∴x+x=40,
解得:x=60﹣20,
∴AA'=(60﹣20)海里,
即此时“昆明舰”的航行距离为(60﹣20)海里.
1.重庆实验外国语学校坐落在美丽且有灵气的华岩寺旁边,特别是金灿灿的大佛让身高1.6米的小王同学很感兴趣,刚刚学过三角函数知识,他就想测一下大佛的高度,小王到A点测得佛顶仰角为37°,接着向大佛走了10米来到B处,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C处,此时与大佛的水平距离DH=6.2米(其中点A、B、C、E、F在同一平面内,点A、B、F在同一条直线上),请问大佛的高度EF为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80).
A.15米 B.16米 C.17米 D.18米
2.如图,小明为了测量照母山上“览星塔”AB的高度,先从与塔底中心B在同一水平面上的点D出发,沿着坡度为1:0.75的斜坡DE行走10米至坡顶E处,再从E处沿水平方向继续前行若干米后至点F处,在F点测得塔顶A的仰角为63°,塔底C的俯角为45°,B与C的水平距离为4米(图中A、B、C、D、E、F在同一平面内,E、F和D、C、B分别在同一水平线上),根据小明的测量数据,计算出“览星塔”AB的高度约为(计算结果精确到0.1米,参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)( )
A.17.8米 B.23.7米 C.31.5米 D.37.4米
3.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
4.如图,在某居民楼AB楼顶有一广告牌BC,在距楼底A点左侧水平距离30m的D点处有一个山坡,山坡DE的坡度(或坡比)i=1:2.4,山坡坡底D点到坡顶E点的距离DE=26m,在坡底D点处测得居民楼楼顶B点的仰角为45°,在坡顶E点处测得居民楼楼顶广告牌上端C点的仰角为27°,居民楼AB,广告牌BC与山坡DE的剖面在同一平面内,则广告牌BC的高度约为( )(结果精确到0.1,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.4.5m B.4.8m C.7.1m D.7.5m
5.如图,在国旗台DF上有一根旗杆AF,国庆节当天小明参加升旗仪式,在B处测得旗杆顶端的仰角为37°,小明向前走4米到达点E,经过坡度为1的坡面DE,坡面的水平距离是1米,到达点D,测得此时旗杆顶端的仰角为53°,则旗杆的高度约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6.29 B.4.71 C.4 D.5.33
6.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度为i=1:2.4,坡长为26米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为( )米(结果精确到1米)(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)
A.27 B.28 C.29 D.30
7.如图,学校某数学兴趣小组想测量操场对面旗杆AB的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,已知旗杆AB所在平台BF的高度为3.5米,则旗杆的高度AB为( )(结果精确到0.1,参考数据:tan35°≈0.7,tan65°≈2.1).
A.19.8米 B.19.7米 C.18.3米 D.16.2米
8.如图,小明站在距一棵树(CD)20m的点B处,小明的眼睛(点A)与地面的距离为1.6m,测得树梢(点C)的仰角为28°,那么这棵树的高度为( )
A.20tan28°m B.20sin28°m
C.(20tan28°+1.6)m D.(20sin28°+1.6)m
9.如图,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28km/时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,此时,灯塔M与渔船的距离是( )
A.7km B.14km C.7km D.14km
10.如图,大楼高30m,远处有一塔BC,某人爬到楼顶D测得塔顶的仰角为30°,且测得D、B相距30m,则塔高BC为( )m.
A.40 B.45 C.30+ D.30
11.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
12.在数学综合实践课上,老师和同学们一起测量学校旗杆的高度,他们首先在旗杆底部C地测得旗杆顶部A的仰角为45°,然后沿着斜坡CD到斜坡顶部D点处再测得旗杆顶部A的仰角为37°(身高忽略不计),已知斜坡CD的坡度i=1:2.4,坡面CD长2.6米,旗杆AB所在旗台高度为1.4米,旗杆、旗台底部、斜坡在同一平面,则旗杆AB的高度为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.9.5米 B.9.6米 C.9.7米 D.9.8米
13.如图,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距( )
A.m(cosα+sinα)米 B.m(cosα﹣sinα)米
C.米 D.米
14.如图,在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )km.
A. B. C. D.2
15.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )
A.100m B.100m C.100m D.m
16.如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为 米.
17.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为 .
18.在高为100米的楼顶测得地面上某十字路口的俯角为60°,那么楼底到这十字路口的水平距离是 米.
19.如图,点P、A、B、C在同一平面内,点A、B、C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为 千米.
20.如图,为了测量塔CD的高度,小明在A处仰望塔顶,测得仰角为30°,再往塔的方向前进60m至B处,测得仰角为60°,那么塔的高度是 m.(小明的身高忽略不计,结果保留根号).
21.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为 m.(结果保留根号)
22.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC= 米(结果保留根号).
23.在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距 千米.(结果精确到0.1千米,参考数据:≈1.414,≈1.732)
24.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为 海里.
25.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为 .(参考数据:tan37°≈,tan53°≈)
26.如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球“的宣传牌,已知立杆AB的高度是4m,从地面上某处D点测得宣传牌顶端C和底端B点的仰角分别是62°和45°、求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
27.如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=50m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,求居民楼AB的高度.(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
28.为了测量建筑物的高度AB,兴趣小组在C处用高为1.5米的测角仪CD,测得屋顶B的仰角为45°,再向房屋方向前进15米,又测得房屋的顶端B的仰角为61°,求房屋的高度AB.(参考数据sin61°≈0.87,tan61°≈1.80,结果保留整数)
29.如图,一艘渔船沿南偏东42°方向航行,在A处测得一个小岛P在其南偏东64°方向.又继续航行(40﹣16)海里到达B处,测得小岛P位于渔船的南偏东72°方向,已知以小岛P为圆心,半径16海里的圆形海域内有暗礁.如果渔船不改变航向有没有触礁的危险,请通过计算加以说明.如果有危险,渔船自B处开始,沿南偏东多少度的方向航行,能够安全通过这一海域?(参考数据:sin22°=,cos22°=,tan22°=)
30.如图,052D型驱逐舰“昆明舰”执行任务后正返回葫芦岛军港C,途经渤海海域A处时,葫芦岛军港C的中国海军发现点A在南偏东30°方向上,旅顺军港B的中国海军发现点A在正西方向上.已知军港C在军港B的北偏西60°方向,且B、C两地相距120海里.(计算结果保留根号)
(1)求出此时点A到军港C的距离;
(2)若“昆明舰”从A处沿AC方向向军港C驶去,当到达点A′时,测得军港B在A′的南偏东75°的方向上,求此时“昆明舰”的航行距离.
参考答案
1.解:过点C作CM⊥BF于点M,过点G作GN⊥EF于点N,
∵斜坡BC的坡度i=4:3,BC=5米,
∴设CM=4x,BM=3x,
∴(4x)2+(3x)2=52,
解得x=1,
∴CM=4米,BM=3米,
由题意可知四边形DHFM和四边形AGNF是矩形,
∴DH=FM=6.2米,
∵AB=10米,
∴AF=GN=AB+BM+MF=10+3+6.2=19.2米,
在Rt△ENG中,∵∠EGN=37°,
∴tan37°=≈0.75,
∴EN=0.75×NG=0.75×19.2=14.4米,
∴EF=EN+NF=14.4+1.6=16米.
故选:B.
2.解:过F作FG⊥AB于G,过C作CH⊥FG于H,如图所示:
则PE=CH=BG,GH=BC=4,
∵斜坡DE的坡度为1:0.75,
∴==,
设PD=3x,则PE=4x,
在Rt△PDE中,由勾股定理得:DE==5x,
∴5x=10,
∴x=2,
∴CH=BG=PE=8,
∵∠CFH=45°,
∴△CFH是等腰直角三角形,
∴FH=CH=8,
∴FG=FH+GH=12,
在Rt△AFG中,tan∠AFG=,
∴AG=FG×tan63°≈12×1.96=23.52,
∴AB=AG+BG=23.52+8=31.5(米),
即“览星塔”AB的高度约为31.5米,
故选:C.
3.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC tanα=2tanα,
故选:B.
4.解:作EF⊥AB于F,作DG⊥EF于G,如图所示:
则GF=AD=30m,AF=DG,∠CEF=27°,
∵山坡DE的坡度i==,
∴EG=2.4DG,
∵DE=26m,DE2+EG2=DE2,
∴AF=DG=10m,EG=24m,
∴EF=EG+GF=54m,
在Rt△CEF中,tan∠CEF==tan27°≈0.51,
∴CF≈0.51×54=27.54(m),
∴AC=AF+CF=10+27.54=37.54(m),
又∵∠ADB=45°,∠A=90°,
∴△ABD是等腰直角三角形,
∴AB=AD=30m,
∴BC=AC﹣AB=37.54﹣30≈7.5(m);
故选:D.
5.解:过点D作DM⊥BC,垂足为M,由题意得,
∠B=37°,∠ADF=53°,BE=4,EM=1,
∵坡面DE的坡度为1,
∴=1,
∴DM=EM=1=FC,
在Rt△ADF中,∠DAF=90°﹣∠ADF=90°﹣53°=37°,
∵tan∠DAF=≈0.75,
设AF=x,则DF=0.75x=MC,
在Rt△ABC中,
∵tan∠B=,
∴tan37°=≈0.75,
解得x=≈6.29(米),
故选:A.
6.解:如图,延长AB交ED的延长线于F,作CG⊥EF于G,
由题意得:FG=BC=20米,DE=40米,BF=CG,
在Rt△CDG中,i=1:2.4,CD=26米,
∴BF=CG=10米,GD=24米,
在Rt△AFE中,∠AFE=90°,FE=FG+GD+DE=84米,∠E=24°,
∴AF=FE tan24°≈84×0.45=37.8(米),
∴AB=AF﹣BF=37.8﹣10≈28(米);
即建筑物AB的高度为28米;
故选:B.
7.解:作CG⊥AF于G,DH⊥CG于H,如图所示:
则HG=DF,FG=DH,
∵楼梯CD的坡度为3:4,CD=3.5,
∴FG=DH=2.1,CH=2.8,
在Rt△ACG中,∠ACG=35°,tan∠ACG==tan35°≈0.7,
∴AG≈0.7CG,
∴AF=AG+FG=0.7CG+2.1,
∵DF=HG=CG﹣CH=CG﹣2.8,
∴EF=DF﹣DE=CG﹣2.8﹣15=CG﹣17.8,
在Rt△AEF中,∠AEF=65°,tan∠AEF==tan65°≈2.1,
∴AF=2.1EF,
∴0.7CG+2.1=2.1(CG﹣17.8),
解得:CG=28.2,
∴AF=0.7×28.2+2.1=21.84,
∴AB=AF﹣BF=21.84﹣3.5≈18.3(米),
即旗杆的高度AB约为18.3米;
故选:C.
8.解:作AE⊥CD于E,如图所示:
则ED=AB=1.6m,AE=BD=20m,
在Rt△ACE中,∠CAE=28°,
∵tan∠CAE=,
∴CE=AE×tan∠CAE=20tan28°,
∴CD=CE+ED=(20tan28°+1.6)m;
故选:C.
9.解:如图,过点M作MC⊥AB于点C,过点B作BN⊥AM于点N,
由题意得,∠MAB=30°,∠MBC=75°,
∵∠CBM=∠BAM+∠AMB,
∴∠AMB=∠NAM=45°,
∴BN=MN,
∵AB=28×0.5=14km,
∴BN==7km,
∴BM=NB=7(km).
故选:A.
10.解:过点D作DE⊥BC于点E,
∵∠BDE=30°,BD=30m,
∴BE=BD=15m,
∵AD=30m,
∴CE=30m,
∴BC=CE+BE=30+15=45m.
故选:B.
11.解:如图,过点D作DE⊥AC于点E,DF⊥AB于点F,
根据题意可知:
BA⊥AC,
∴四边形FAED是矩形,
∴FA=DE,DF=AE,
∵斜坡CD的长为6m,坡度i=DE:CE=1:0.75,
∴DE=4.8,CE=3.6,
∴DF=AE=AC+CE=11.6,
在Rt△BFD中,∠BDF=46°,
∴BF=DF tan46°≈11.6×1.04≈12.064,
∴BA=BF+FA=12.064+4.8≈16.9(m).
所以教学楼的高度约为16.9米.
故选:C.
12.解:作DH⊥FC交FC的延长线于点H,延长AB交CF的延长线于点T,作DJ⊥AT于点J,如图所示:
则四边形EFTB与四边形DHTJ都是矩形,
∴BT=EF=1.4米,JT=DH,
在Rt△DCH中,CD=2.6米,=,
∴DH=1(米),CH=2.4(米),
∵∠ACT=45°,∠T=90°,
∴AT=TC,
设AT=TC=x.则DJ=TH=(x+2.4)米,AJ=(x﹣1)米,
在Rt△ADJ中,tan∠ADJ==0.75,
∴=0.75,
解得:x=11.2,
∴AB=AT﹣BT=11.2﹣1.4=9.8(米),
故选:D.
13.解:过点C作CD⊥AB于D,如图所示:
由题意得:∠ACD=45°,∠DCB=α,
在Rt△BCD中,BC=m,
∴DB=BCsinα°=m sinα(米),CD=BCcosα=m cosα(米),
在Rt△ACD中,AD=CD=m cosα(米),
∴AB=AD+DB=m(cosα+sinα)(米).
故选:A.
14.解:过点C作CD⊥AB于点D,
根据题意得:∠CAD=90°﹣60°=30°,
∠CBD=90°﹣30°=60°,
∴∠ACB=∠CBD﹣∠CAD=30°,
∴∠CAB=∠ACB,
∴BC=AB=3km,
在Rt△CBD中,
∴CD=BC sin60°=3×(km).
∴船C到海岸线l的距离是km.
故选:C.
15.解:由题意得,∠AOB=90°﹣60°=30°,
∴AB=OA=100(m),
故选:A.
16.解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=AM=25米;
故答案为:25.
17.解:由题意得:∠BAC=31°,∠CBD=45°,
∵∠CBD=∠BAC+∠ACB,
∴∠ACB=∠CBD﹣∠BAC=45°﹣31°=14°,
故答案为:14°.
18.解:如图所示:
由题意得:∠B=90°,∠BAC=60°,BC=100米,
∵tan∠BAC=,
∴AB===(米),
即楼底到这十字路口的水平距离是米,
故答案为:.
19.解:∵PC⊥AC,在点A处测得点P在北偏东60°方向上,
∴∠PCA=90°,∠PAC=30°,
∵AP=12千米,
∴PC=6千米,AC=6千米,
∵在点B处测得点P在北偏东30°方向上,∠PCB=90°,PC=6千米,
∴∠PBC=60°,
∴BC===2千米,
∴AB=AC﹣BC=6﹣2=4(千米),
故答案为:4千米.
20.解:∵∠DAB=30°,∠DBC=60°,
∴BD=AB=60m.
∴DC=BD sin60°=60×=30(m),
答:该塔高为30m,
故答案为:30.
21.解:∵在Rt△ABD中,AD=90,∠BAD=45°,
∴BD=AD=30(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD tan60°=30×=30(m),
∴BC=BD+CD=30+30(m)
答:该建筑物的高度BC约为(30+30)米.
故答案为:(30+30).
22.解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米);
故答案为:(100+100).
23.解:∵B在A的正东方,C在A地的北偏东 60°方向,
∴∠BAC=90°﹣60°=30°,
∵C在B地的北偏东15°方向,
∴∠ABC=90°+15°=105°,
∴∠C=180°﹣∠BAC﹣∠ABC=180°﹣30°﹣105°=45°,
过B作BD⊥AC于D,
在Rt△ABD中,∠BAD=30°,AB=4km,
∴BD=AB=2km,AD=2km,
在Rt△BCD中,∠C=45°,
∴CD=BD=2km,
∴AC=AD+CD=(2+2)≈5.5km,
答:A、C两地相距5.5千米,
故答案为:5.5.
24.解:根据题意得:∠BAC=90°,AB=12海里,AC=9海里,
在Rt△ABC中,BC==15海里,
故答案为:15.
25.解:如图,作CE⊥BA于E.设EC=xm,BE=ym.
在Rt△ECB中,tan53°=,即,
在Rt△AEC中,tan37°=,即,
解得x=180,y=135,
∴AC===300(m),
故答案为:300m.
26.解:在Rt△ADB中,
∵∠BDA=45°,
∴AD=AB=4m.
在Rt△ADC中,AC=AD tan62°≈4×1.88=7.52(m).
∴BC=AC﹣AB=7.52﹣4=3.52≈3.5(m).
答:宣传牌BC的高度是3.5m.
27.解:如图,过点D作DF⊥AB,垂足为F,作DE⊥BC交BC的延长线于点E,
由题意得,∠ADF=28°,CD=50m,BC=60m,
在Rt△DEC中,
∵山坡CD的坡度i=1:0.75,
∴==,
设DE=4xm,则EC=3xm,由勾股定理可得CD=5xm,
又CD=50m,即5x=50,
∴x=10(m),
∴EC=3x=30(m),DE=4x=40(m)=FB,
∴BE=BC+EC=60+30=90(m)=DF,
在Rt△ADF中,
AF=tan28°×DF≈0.53×90≈47.7(m),
∴AB=AF+FB=47.7+40≈87.7(m),
即居民楼AB的高度约为87.7m.
28.解:由题意得,四边形DCEF,四边形MAEF都是矩形,
所以,AM=EF=CD=1.5米,DF=CE=15米,
设BM=x米,
在Rt△BMF中,
tan∠BFM=tan61°=≈1.80,
∴FM=,
在Rt△BDM中,
tan∠BDM=tan45°==1,
∴DM=BM=x,
∵DM=DF+FM,
∴x=15+,
解得,x=33.75,
∴AB=AM+BM=1.5+33.75≈35(米),
答:房屋的高度AB约为35米.
29.解:如图1,过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=64°﹣42°=22°,∠PBC=72°﹣42°=30°,AB=40﹣16,
设PC=x,
在Rt△PBC中,
∵∠PBC=30°,
∴BC=PC=x,
∴AC=AB+BC=40﹣16+x,
在Rt△PAC中,
∵∠PAC=22°,
∴tan∠PAC=,即=,
解得,x=16,即PC=16,BP=2PC=32,
∵16<16,
∴有危险.
如图2,渔船沿着BD方向航行,过点P作PD⊥BD,垂足为D,
在Rt△PBD中,
∵sin∠PBD===,
∴∠PBD=45°,
∴∠QBD=∠QBP﹣∠DBP=72°﹣45°=27°,
即渔船自B处开始,沿南偏东27°的方向航行,能够安全通过这一海域.
30.解:(1)如图所示:延长BA,过点C作CD⊥BA延长线与点D,
由题意可得:∠CBD=30°,BC=120海里,
则CD=BC=60海里,
∵cos∠ACD==cos30°=,
即=
∴AC=40(海里),
即此时点A到军港C的距离为40海里;
(2)过点A′作A′N⊥BC于点N,如图:
由(1)得:CD=60海里,AC=40海里,
∵A'E∥CD,
∴∠AA'E=∠ACD=30°,
∴∠BA′A=45°,
∵∠BA'E=75°,
∴∠ABA'=15°,
∴∠2=15°=∠ABA',
即A′B平分∠CBA,
∴A'E=A'N,
设AA′=x,则AE=AA',A'N=A′E=AE=x,
∵∠1=60°﹣30°=30°,A'N⊥BC,
∴A'C=2A'N=x,
∵A'C+AA'=AC,
∴x+x=40,
解得:x=60﹣20,
∴AA'=(60﹣20)海里,
即此时“昆明舰”的航行距离为(60﹣20)海里.
