人教版2021—2022学年数学九年级上册24.4弧长与扇形面积-求不规则图像面积训练(word版、含答案)
文档属性
| 名称 | 人教版2021—2022学年数学九年级上册24.4弧长与扇形面积-求不规则图像面积训练(word版、含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 549.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 14:30:26 | ||
图片预览


文档简介
人教版九年级上册数学24.4弧长与扇形面积-求不规则图像面积训练
一、单选题
1.如图,是的直径,弦,垂足为, ,,则等于( )
A. B. C. D.
2.如图,在中,,,以的中点为圆心,作圆心角为的扇形,点恰在上,设,当由小到大变化时,图中阴影部分的面积为( )
A. B. C. D.随的变化而变化
3.一个商标图案如图中阴影部分,在长方形中,,,以点为圆心,为半径作圆与的延长线相交于点,则商标图案的面积是( )
A. B.
C. D.
4.如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC于点D,则图中阴影部分的面积是( )
A.2﹣ B.2﹣ C.4﹣ D.4﹣
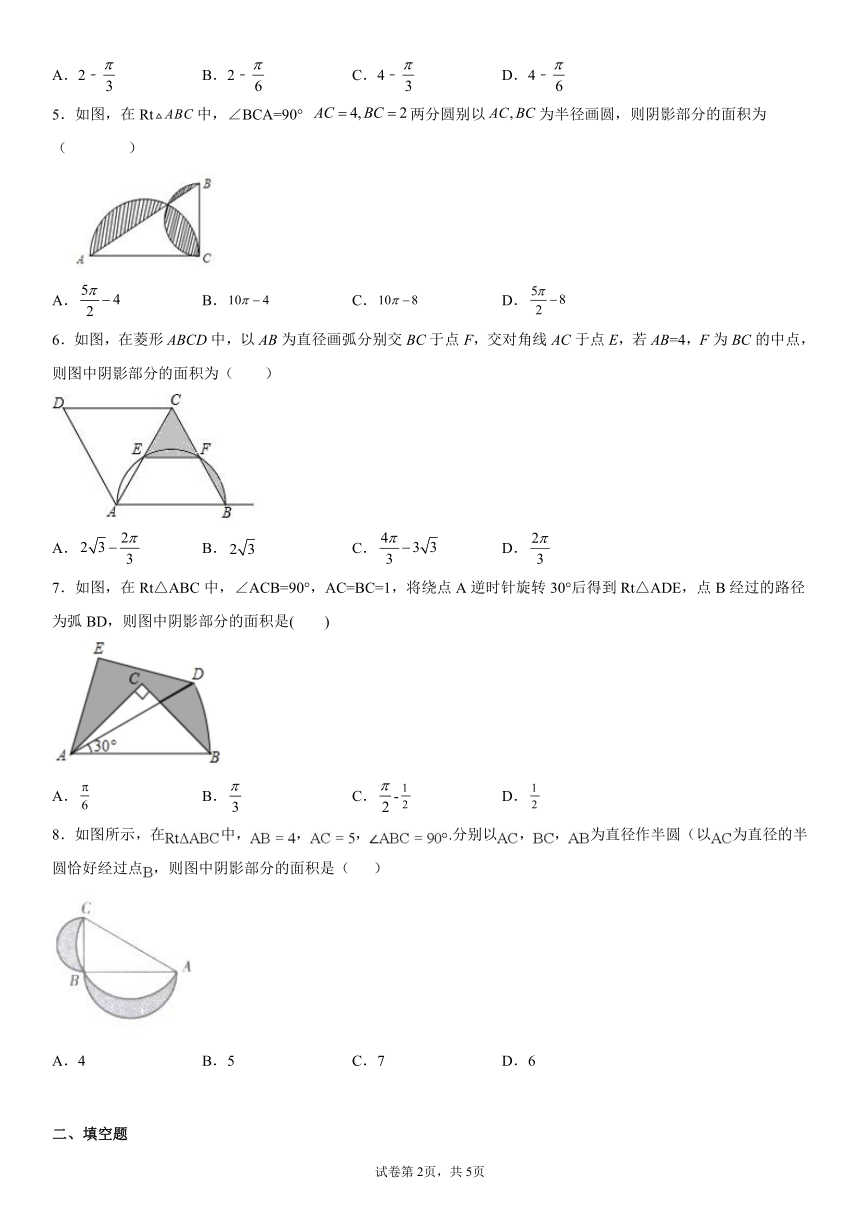
5.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
6.如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是( )
A. B. C.- D.
8.如图所示,在中,,,.分别以,,为直径作半圆(以为直径的半圆恰好经过点,则图中阴影部分的面积是( )
A.4 B.5 C.7 D.6
二、填空题
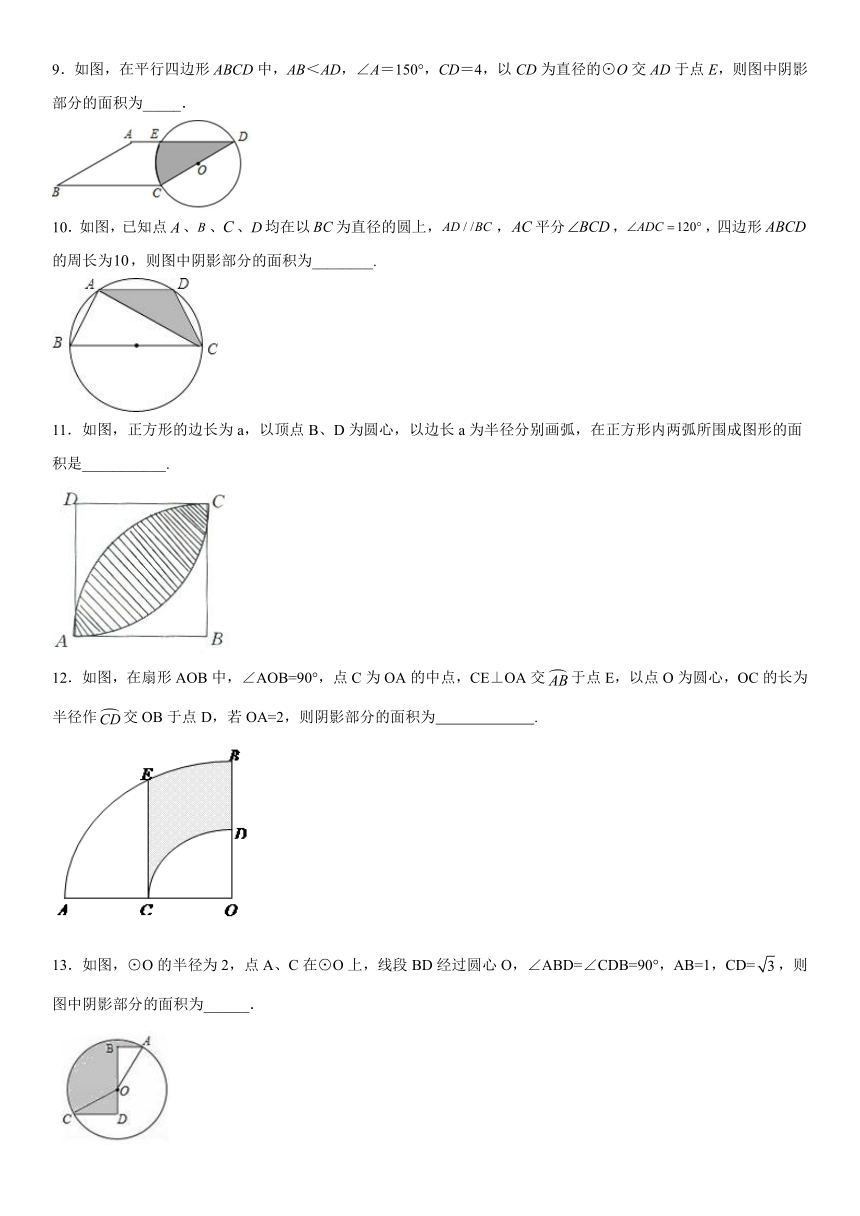
9.如图,在平行四边形ABCD中,AB<AD,∠A=150°,CD=4,以CD为直径的⊙O交AD于点E,则图中阴影部分的面积为_____.
10.如图,已知点、、、均在以为直径的圆上,,平分,,四边形的周长为,则图中阴影部分的面积为________.
11.如图,正方形的边长为a,以顶点B、D为圆心,以边长a为半径分别画弧,在正方形内两弧所围成图形的面积是___________.
12.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D,若OA=2,则阴影部分的面积为 .
13.如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=,则图中阴影部分的面积为______.
14.如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是______(结果保留)
15.如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=,∠P=60°,则图中阴影部分的面积为____.
三、解答题
16.如图,正方形的边长为a,以各边为直径在正方形内画半圆.求图中阴影部分的面积.
17.如图所示,,.
(1)已知,求以为直径的半圆面积及扇形的面积;
(2)若的长度未知,已知阴影甲的面积为16平方厘米,能否求阴影乙的面积?若能,请直接写出结果;若不能,请说明理由.
18.如图,半圆O的直径AB为40,C,D是这个半圆的三等分点,求弦AC,AD和弧CD围成的阴影部分的面积.
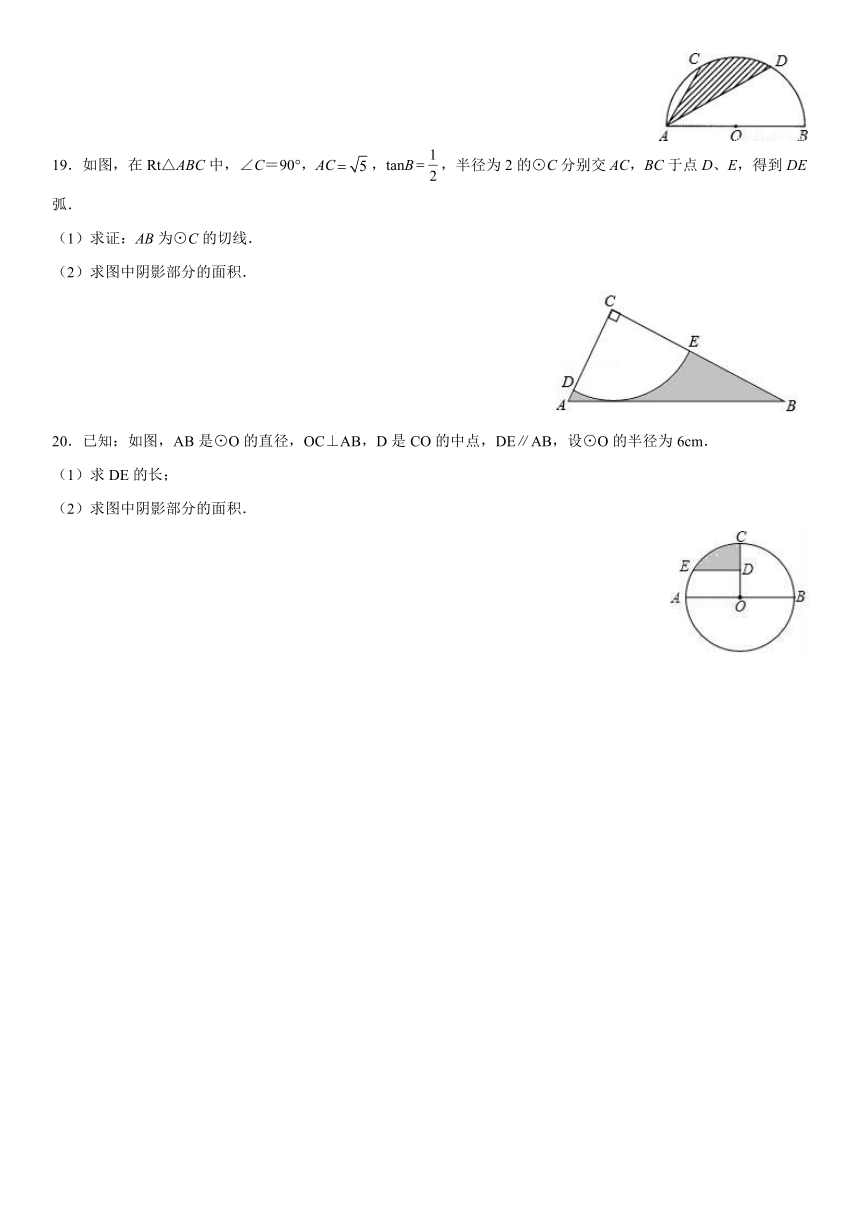
19.如图,在Rt△ABC中,∠C=90°,AC,tanB,半径为2的⊙C分别交AC,BC于点D、E,得到DE弧.
(1)求证:AB为⊙C的切线.
(2)求图中阴影部分的面积.
20.已知:如图,AB是⊙O的直径,OC⊥AB,D是CO的中点,DE∥AB,设⊙O的半径为6cm.
(1)求DE的长;
(2)求图中阴影部分的面积.
参考答案
1.D
2.C
3.D
4.A
5.A
6.D
7.A
8.D
9.
10.
11.
12..
13.
14.
15.
16.
解:如图,图中四个半圆都通过正方形的中心,用正方形的面积减去四空白的面积,剩下的就是阴影部分的面积,而正方形的面积减去两个半圆的面积就得两个空隙的面积,
∴,
∴
∴
17.
(1)因为OB=20,
所以S半圆=×(20÷2)2,
=×100,
≈157;
S扇形BOC=××R2,
=××202,
≈157;
答:半圆面积是157,扇形COB的面积是157.
(2)能求阴影乙的面积:
因为,∠AOB=90°,∠COB=45°,
所以半圆的直径OB,△BOD的底是OB,
高是半圆的半径即OB,
所以S半圆=×OB×OB,
=OB2;
S扇形BOC=××OB2,
=××OB2;
=OB2;
所以S半圆=S扇形BOC,
S半圆 ①=S扇形 ①,
所以S甲=S乙,
因为S甲=16平方厘米,
所以S乙=16平方厘米,
答:阴影乙的面积是16平方厘米.
18.
试题解析:连接CO、OD,CD,如图;
∵C、D是这个半圆的三等分点,
∴CD∥AB,∠CDO=60°,
∴∠CAD的度数为:30°,
∵OC=OD,∴△OCD是等边三角形,CD=OC=AB=20,
∴△OCD与△CDA是等底等高的三角形,
∴S阴影=S扇形OCD=π×202=400πcm2.
答:阴影部分的面积S是400πcm2.
19.
【详解】
(1)过C作CF⊥AB于F.
∵在Rt△ABC中,∠C=90°,AC,tanB,∴BC=2,由勾股定理得:AB5.
∵△ACB的面积S,∴CF2,∴CF为⊙C的半径.
∵CF⊥AB,∴AB为⊙C的切线;
(2)图中阴影部分的面积=S△ACB﹣S扇形DCE5﹣π.
20.
解:(1)连接OE.
∵D是CO的中点,⊙O的半径为6cm,
∴OD=OC=3cm.
∵OC⊥AB,DE∥AB,
∴∠ODE=90°,
∴DE==3;
(2)∵OD=OC,∠ODE=90°,
∴∠OED=30°,
∴∠DOE=60°,
∴图中阴影部分的面积=﹣×3×3=6π﹣(cm2).
试卷第2页,共2页
一、单选题
1.如图,是的直径,弦,垂足为, ,,则等于( )
A. B. C. D.
2.如图,在中,,,以的中点为圆心,作圆心角为的扇形,点恰在上,设,当由小到大变化时,图中阴影部分的面积为( )
A. B. C. D.随的变化而变化
3.一个商标图案如图中阴影部分,在长方形中,,,以点为圆心,为半径作圆与的延长线相交于点,则商标图案的面积是( )
A. B.
C. D.
4.如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC于点D,则图中阴影部分的面积是( )
A.2﹣ B.2﹣ C.4﹣ D.4﹣
5.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
6.如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是( )
A. B. C.- D.
8.如图所示,在中,,,.分别以,,为直径作半圆(以为直径的半圆恰好经过点,则图中阴影部分的面积是( )
A.4 B.5 C.7 D.6
二、填空题
9.如图,在平行四边形ABCD中,AB<AD,∠A=150°,CD=4,以CD为直径的⊙O交AD于点E,则图中阴影部分的面积为_____.
10.如图,已知点、、、均在以为直径的圆上,,平分,,四边形的周长为,则图中阴影部分的面积为________.
11.如图,正方形的边长为a,以顶点B、D为圆心,以边长a为半径分别画弧,在正方形内两弧所围成图形的面积是___________.
12.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D,若OA=2,则阴影部分的面积为 .
13.如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=,则图中阴影部分的面积为______.
14.如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是______(结果保留)
15.如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=,∠P=60°,则图中阴影部分的面积为____.
三、解答题
16.如图,正方形的边长为a,以各边为直径在正方形内画半圆.求图中阴影部分的面积.
17.如图所示,,.
(1)已知,求以为直径的半圆面积及扇形的面积;
(2)若的长度未知,已知阴影甲的面积为16平方厘米,能否求阴影乙的面积?若能,请直接写出结果;若不能,请说明理由.
18.如图,半圆O的直径AB为40,C,D是这个半圆的三等分点,求弦AC,AD和弧CD围成的阴影部分的面积.
19.如图,在Rt△ABC中,∠C=90°,AC,tanB,半径为2的⊙C分别交AC,BC于点D、E,得到DE弧.
(1)求证:AB为⊙C的切线.
(2)求图中阴影部分的面积.
20.已知:如图,AB是⊙O的直径,OC⊥AB,D是CO的中点,DE∥AB,设⊙O的半径为6cm.
(1)求DE的长;
(2)求图中阴影部分的面积.
参考答案
1.D
2.C
3.D
4.A
5.A
6.D
7.A
8.D
9.
10.
11.
12..
13.
14.
15.
16.
解:如图,图中四个半圆都通过正方形的中心,用正方形的面积减去四空白的面积,剩下的就是阴影部分的面积,而正方形的面积减去两个半圆的面积就得两个空隙的面积,
∴,
∴
∴
17.
(1)因为OB=20,
所以S半圆=×(20÷2)2,
=×100,
≈157;
S扇形BOC=××R2,
=××202,
≈157;
答:半圆面积是157,扇形COB的面积是157.
(2)能求阴影乙的面积:
因为,∠AOB=90°,∠COB=45°,
所以半圆的直径OB,△BOD的底是OB,
高是半圆的半径即OB,
所以S半圆=×OB×OB,
=OB2;
S扇形BOC=××OB2,
=××OB2;
=OB2;
所以S半圆=S扇形BOC,
S半圆 ①=S扇形 ①,
所以S甲=S乙,
因为S甲=16平方厘米,
所以S乙=16平方厘米,
答:阴影乙的面积是16平方厘米.
18.
试题解析:连接CO、OD,CD,如图;
∵C、D是这个半圆的三等分点,
∴CD∥AB,∠CDO=60°,
∴∠CAD的度数为:30°,
∵OC=OD,∴△OCD是等边三角形,CD=OC=AB=20,
∴△OCD与△CDA是等底等高的三角形,
∴S阴影=S扇形OCD=π×202=400πcm2.
答:阴影部分的面积S是400πcm2.
19.
【详解】
(1)过C作CF⊥AB于F.
∵在Rt△ABC中,∠C=90°,AC,tanB,∴BC=2,由勾股定理得:AB5.
∵△ACB的面积S,∴CF2,∴CF为⊙C的半径.
∵CF⊥AB,∴AB为⊙C的切线;
(2)图中阴影部分的面积=S△ACB﹣S扇形DCE5﹣π.
20.
解:(1)连接OE.
∵D是CO的中点,⊙O的半径为6cm,
∴OD=OC=3cm.
∵OC⊥AB,DE∥AB,
∴∠ODE=90°,
∴DE==3;
(2)∵OD=OC,∠ODE=90°,
∴∠OED=30°,
∴∠DOE=60°,
∴图中阴影部分的面积=﹣×3×3=6π﹣(cm2).
试卷第2页,共2页
同课章节目录
