2021-2022学年鲁教版(五四制)数学九年级上册3.1 对函数的再认识 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)数学九年级上册3.1 对函数的再认识 同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 150.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 19:30:20 | ||
图片预览

文档简介
对函数的再认识
一、选择题
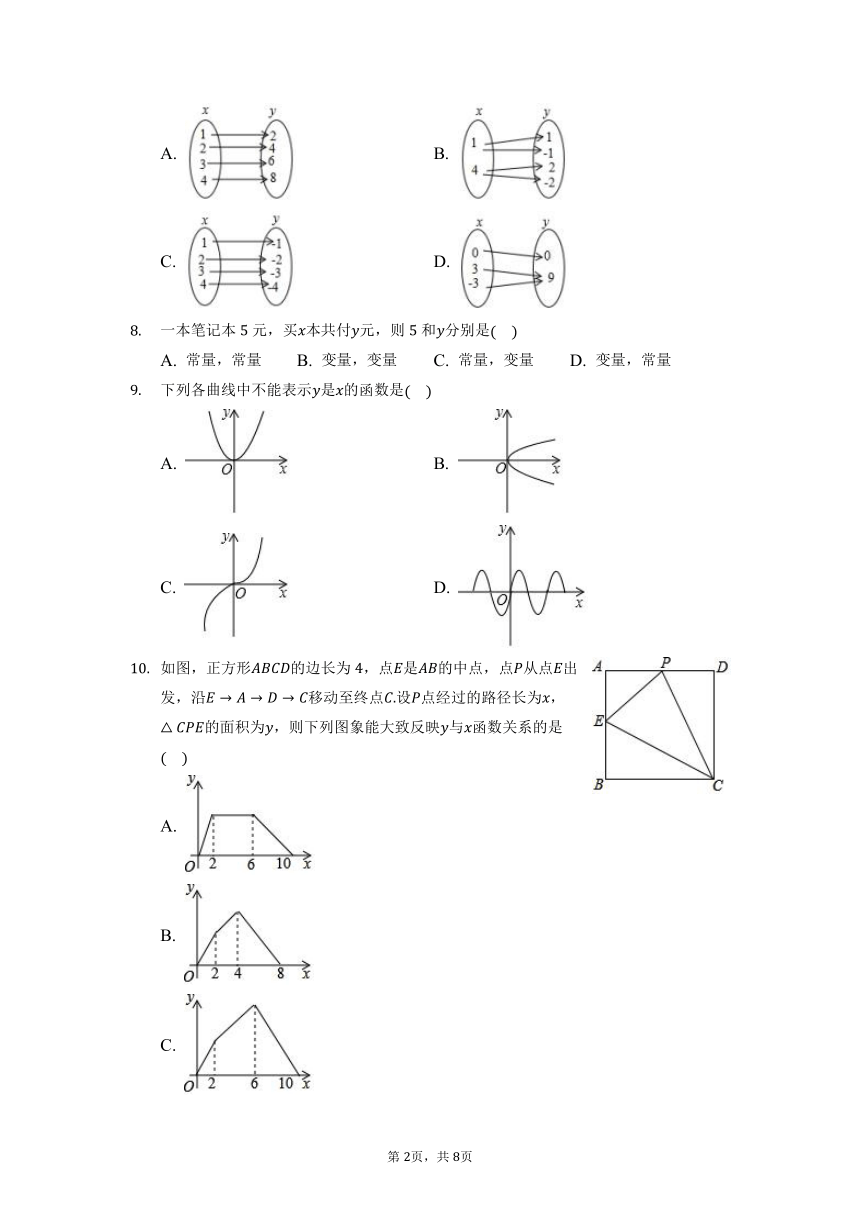
从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是
A. 物体 B. 速度 C. 时间 D. 空气
下列关系式中,不是的函数的是
A. B. C. D.
假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是
行驶速度;行驶时间;行驶路程;汽车油箱中的剩余油量.
A. 个 B. 个 C. 个 D. 个
在函数中,自变量的取值范围是
A. B.
C. 且 D.
如图甲,、是半径为的上两点,且点从出发,在上以每秒一个单位的速度匀速运动,回到点运动结束.设运动时间为,弦的长度为,那么如图乙图象中可能表示与的函数关系的是
A. B. C. 或 D. 或
已知二次函数,当时,的值为
A. B. C. D.
下列关于变量,的关系,其中不是的函数的是
A. B.
C. D.
一本笔记本元,买本共付元,则和分别是
A. 常量,常量 B. 变量,变量 C. 常量,变量 D. 变量,常量
下列各曲线中不能表示是的函数是
A. B.
C. D.
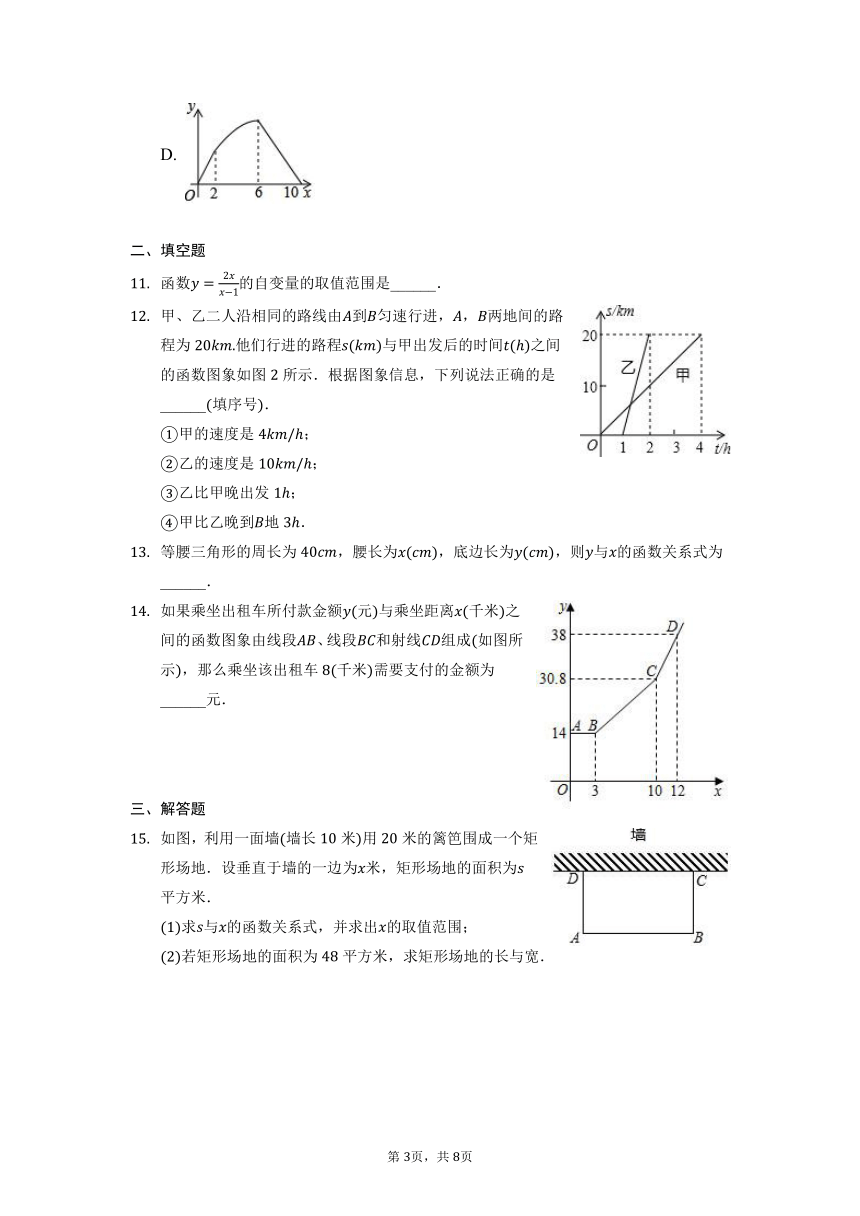
如图,正方形的边长为,点是的中点,点从点出发,沿移动至终点设点经过的路径长为,的面积为,则下列图象能大致反映与函数关系的是
A.
B.
C.
D.
二、填空题
函数的自变量的取值范围是______.
甲、乙二人沿相同的路线由到匀速行进,,两地间的路程为他们行进的路程与甲出发后的时间之间的函数图象如图所示.根据图象信息,下列说法正确的是______填序号.
甲的速度是;
乙的速度是;
乙比甲晚出发;
甲比乙晚到地.
等腰三角形的周长为,腰长为,底边长为,则与的函数关系式为______.
如果乘坐出租车所付款金额元与乘坐距离千米之间的函数图象由线段、线段和射线组成如图所示,那么乘坐该出租车千米需要支付的金额为______元.
三、解答题
如图,利用一面墙墙长米用米的篱笆围成一个矩形场地.设垂直于墙的一边为米,矩形场地的面积为平方米.
求与的函数关系式,并求出的取值范围;
若矩形场地的面积为平方米,求矩形场地的长与宽.
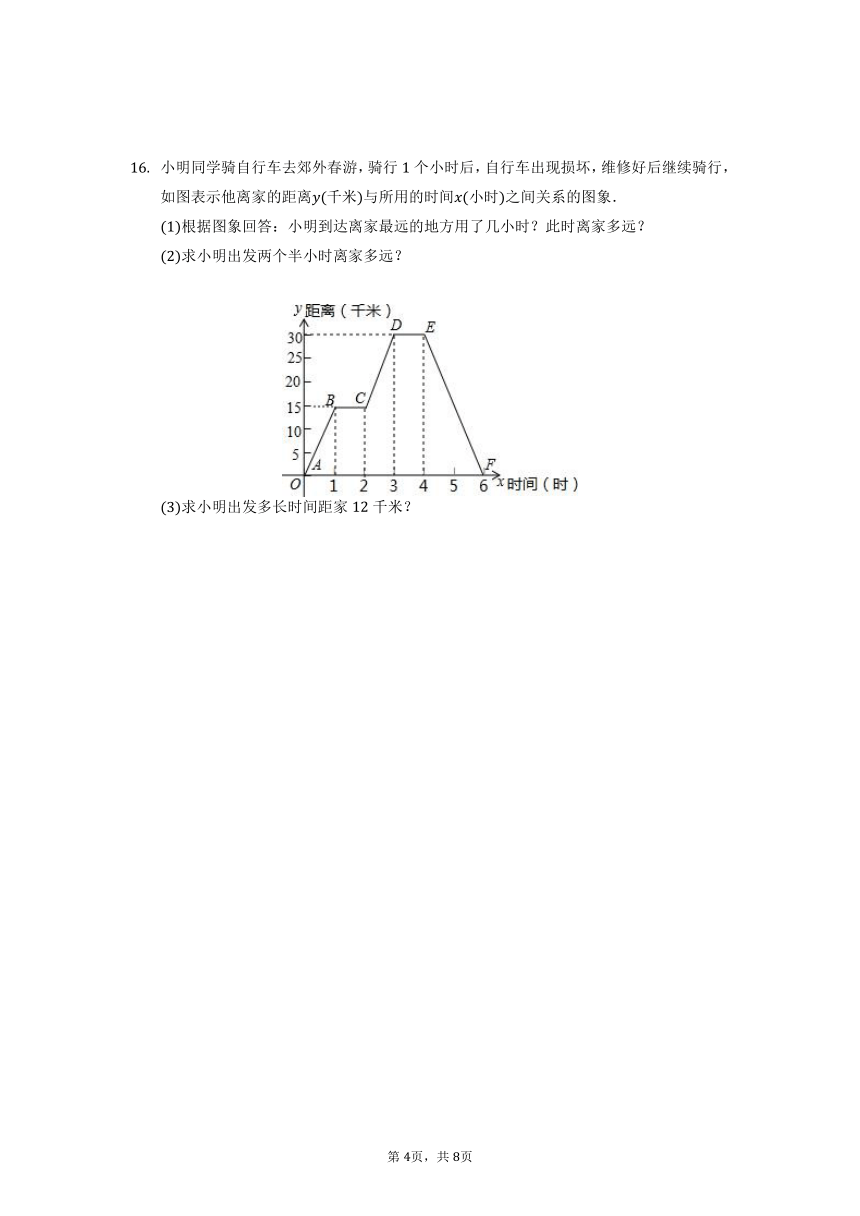
小明同学骑自行车去郊外春游,骑行个小时后,自行车出现损坏,维修好后继续骑行,如图表示他离家的距离千米与所用的时间小时之间关系的图象.
根据图象回答:小明到达离家最远的地方用了几小时?此时离家多远?
求小明出发两个半小时离家多远?
求小明出发多长时间距家千米?
答案和解析
1.【答案】
【解析】解:因为速度随时间的变化而变化,
故时间是自变量,速度是因变量,
即速度是时间的函数.
2.【答案】
【解析】解:、,是的函数;
B、,是的函数;
C、,是的函数;
D、,对于的每一个确定的值,不是有唯一的值与其对应,
不是的函数;
3.【答案】
【解析】解:汽车匀速行驶在高速公路上,速度是常量,随着时间的变化,行驶时间,行驶路程,剩余油量随之变化,
行驶时间;行驶路程;汽车油箱中的剩余油量是变量.
4.【答案】
【解析】解:根据题意得:,
解得:且 .
5.【答案】
【解析】解:当点顺时针旋转时,图象是,当点逆时针旋转时,图象是,
故答案为,
6.【答案】
【解析】解:把代入二次函数,得
.
7.【答案】
【解析】解:、、当取值时,有唯一的值对应,
8.【答案】
【解答】
解:一本笔记本元,买本共付元,则和分别是常量,变量.
故选:.
9.【答案】
【解析】解:、满足对于的每一个取值,都有唯一确定的值与之对应关系,故A不符合题意;
B、满足对于的每一个取值,有两个值与之对应关系,故B符合题意;
C、满足对于的每一个取值,都有唯一确定的值与之对应关系,故C不符合题意;
D、满足对于的每一个取值,都有唯一确定的值与之对应关系,故D不符合题意;
10.【答案】
【解析】解:通过已知条件可知,当点与点重合时,的面积为;
当点在上运动时,的高不变,则的面积是的一次函数,面积随增大而增大,
当时有最大面积为,
当在边上运动时,的底边不变,则的面积是的一次函数,面积随增大而增大,
当时,有最大面积为,
当点在边上运动时,的底边不变,则的面积是的一次函数,面积随增大而减小,最小面积为;
11.【答案】
【解析】解:根据题意,有,
解可得;
故自变量的取值范围是,
故答案为.
根据分式有意义的条件是分母不为,解可得自变量的取值范围.
12.【答案】
【解析】解:由图可知,甲用小时走完全程,可得速度为;
乙比甲晚出发一小时,用小时走完全程,可得速度为.
故答案为:.
由图可得,该图象是路程与时间的关系,乙比甲晚出发一小时且乙的速度比甲的速度快.
13.【答案】
【解析】解:由题意得,,
则,
故答案为:.
14.【答案】
【解析】解:乘坐该出租车千米需要支付的金额为:元.
故答案为:.
根据函数图象中的数据,乘坐距离在千米以内收费为元,大于千米而不大于千米以内的每千米收费为:元,据此列式计算即可解答.
15.【答案】解:,
.
又墙长米,
,
.
.
当矩形场地的面积为平方米时,,
解得:不合题意,舍去,,
.
答:矩形的长为米,宽为米.
16.【答案】解:小明到达离家最远的地方需小时,此时离家千米;
段表示的速度为千米时,
千米,
即小明出发两个半小时离家千米.
段表示的速度为千米时
小时
段表示的速度为千米时
小时
即当小明出发小时或小时时,小明距家千米.
第2页,共2页
第1页,共1页
一、选择题
从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是
A. 物体 B. 速度 C. 时间 D. 空气
下列关系式中,不是的函数的是
A. B. C. D.
假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是
行驶速度;行驶时间;行驶路程;汽车油箱中的剩余油量.
A. 个 B. 个 C. 个 D. 个
在函数中,自变量的取值范围是
A. B.
C. 且 D.
如图甲,、是半径为的上两点,且点从出发,在上以每秒一个单位的速度匀速运动,回到点运动结束.设运动时间为,弦的长度为,那么如图乙图象中可能表示与的函数关系的是
A. B. C. 或 D. 或
已知二次函数,当时,的值为
A. B. C. D.
下列关于变量,的关系,其中不是的函数的是
A. B.
C. D.
一本笔记本元,买本共付元,则和分别是
A. 常量,常量 B. 变量,变量 C. 常量,变量 D. 变量,常量
下列各曲线中不能表示是的函数是
A. B.
C. D.
如图,正方形的边长为,点是的中点,点从点出发,沿移动至终点设点经过的路径长为,的面积为,则下列图象能大致反映与函数关系的是
A.
B.
C.
D.
二、填空题
函数的自变量的取值范围是______.
甲、乙二人沿相同的路线由到匀速行进,,两地间的路程为他们行进的路程与甲出发后的时间之间的函数图象如图所示.根据图象信息,下列说法正确的是______填序号.
甲的速度是;
乙的速度是;
乙比甲晚出发;
甲比乙晚到地.
等腰三角形的周长为,腰长为,底边长为,则与的函数关系式为______.
如果乘坐出租车所付款金额元与乘坐距离千米之间的函数图象由线段、线段和射线组成如图所示,那么乘坐该出租车千米需要支付的金额为______元.
三、解答题
如图,利用一面墙墙长米用米的篱笆围成一个矩形场地.设垂直于墙的一边为米,矩形场地的面积为平方米.
求与的函数关系式,并求出的取值范围;
若矩形场地的面积为平方米,求矩形场地的长与宽.
小明同学骑自行车去郊外春游,骑行个小时后,自行车出现损坏,维修好后继续骑行,如图表示他离家的距离千米与所用的时间小时之间关系的图象.
根据图象回答:小明到达离家最远的地方用了几小时?此时离家多远?
求小明出发两个半小时离家多远?
求小明出发多长时间距家千米?
答案和解析
1.【答案】
【解析】解:因为速度随时间的变化而变化,
故时间是自变量,速度是因变量,
即速度是时间的函数.
2.【答案】
【解析】解:、,是的函数;
B、,是的函数;
C、,是的函数;
D、,对于的每一个确定的值,不是有唯一的值与其对应,
不是的函数;
3.【答案】
【解析】解:汽车匀速行驶在高速公路上,速度是常量,随着时间的变化,行驶时间,行驶路程,剩余油量随之变化,
行驶时间;行驶路程;汽车油箱中的剩余油量是变量.
4.【答案】
【解析】解:根据题意得:,
解得:且 .
5.【答案】
【解析】解:当点顺时针旋转时,图象是,当点逆时针旋转时,图象是,
故答案为,
6.【答案】
【解析】解:把代入二次函数,得
.
7.【答案】
【解析】解:、、当取值时,有唯一的值对应,
8.【答案】
【解答】
解:一本笔记本元,买本共付元,则和分别是常量,变量.
故选:.
9.【答案】
【解析】解:、满足对于的每一个取值,都有唯一确定的值与之对应关系,故A不符合题意;
B、满足对于的每一个取值,有两个值与之对应关系,故B符合题意;
C、满足对于的每一个取值,都有唯一确定的值与之对应关系,故C不符合题意;
D、满足对于的每一个取值,都有唯一确定的值与之对应关系,故D不符合题意;
10.【答案】
【解析】解:通过已知条件可知,当点与点重合时,的面积为;
当点在上运动时,的高不变,则的面积是的一次函数,面积随增大而增大,
当时有最大面积为,
当在边上运动时,的底边不变,则的面积是的一次函数,面积随增大而增大,
当时,有最大面积为,
当点在边上运动时,的底边不变,则的面积是的一次函数,面积随增大而减小,最小面积为;
11.【答案】
【解析】解:根据题意,有,
解可得;
故自变量的取值范围是,
故答案为.
根据分式有意义的条件是分母不为,解可得自变量的取值范围.
12.【答案】
【解析】解:由图可知,甲用小时走完全程,可得速度为;
乙比甲晚出发一小时,用小时走完全程,可得速度为.
故答案为:.
由图可得,该图象是路程与时间的关系,乙比甲晚出发一小时且乙的速度比甲的速度快.
13.【答案】
【解析】解:由题意得,,
则,
故答案为:.
14.【答案】
【解析】解:乘坐该出租车千米需要支付的金额为:元.
故答案为:.
根据函数图象中的数据,乘坐距离在千米以内收费为元,大于千米而不大于千米以内的每千米收费为:元,据此列式计算即可解答.
15.【答案】解:,
.
又墙长米,
,
.
.
当矩形场地的面积为平方米时,,
解得:不合题意,舍去,,
.
答:矩形的长为米,宽为米.
16.【答案】解:小明到达离家最远的地方需小时,此时离家千米;
段表示的速度为千米时,
千米,
即小明出发两个半小时离家千米.
段表示的速度为千米时
小时
段表示的速度为千米时
小时
即当小明出发小时或小时时,小明距家千米.
第2页,共2页
第1页,共1页
