2021-2022学年鲁教版(五四制)数学九年级上册3.6二次函数的应用 同步练习 (Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)数学九年级上册3.6二次函数的应用 同步练习 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 208.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 00:00:00 | ||
图片预览




文档简介
二次函数的应用
一、选择题
赵州桥的桥拱可以用抛物线的一部分表示,函数关系为,当水面宽度为时,水面与桥拱顶的高度等于
A.
B.
C.
D.
在中,,,,,若,则的面积关于边长的函数关系式为
A. B. C. D.
如图是抛物线形拱桥,当拱顶高离水面时,水面宽,水面下降,水面宽度增加
A.
B.
C.
D.
有一个矩形苗圃园,其中一边靠墙,另外边用长为的篱笆围成.已知墙长为,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为
A. ,
B. ,
C. ,
D. ,
长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,则与之间的关系式是
A. B.
C. D.
从地面竖直向上抛出一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示.下列结论:
小球在空中经过的路程是;
小球运动的时间为;
小球抛出秒时,速度为;
当时,小球的高度.
其中正确的是
A. B. C. D.
三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为米,孔顶离水面米;当水位下降,大孔水面宽度为米时,单个小孔的水面宽度为米,若大孔水面宽度为米,则单个小孔的水面宽度为
A. 米 B. 米 C. 米 D. 米
飞机着陆后滑行的距离米关于滑行的时间秒的函数解析式是,则飞机着陆后滑行到停止下来,滑行的距离为
A. 米 B. 米 C. 米 D. 米
一个运动员打高尔夫球,若球的飞行高度与水平距离之间的函数表达式为:,则高尔夫球在飞行过程中的最大高度为.
A. B. C. D.
二、填空
如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面米高时,水面为米,则当水面下降米时,水面宽度增加______米.
如图,有一个矩形苗圃园、其中一边靠墙墙长为,另外三边用长为的篱笆围成,则这个苗圃园面积的最大值为______.
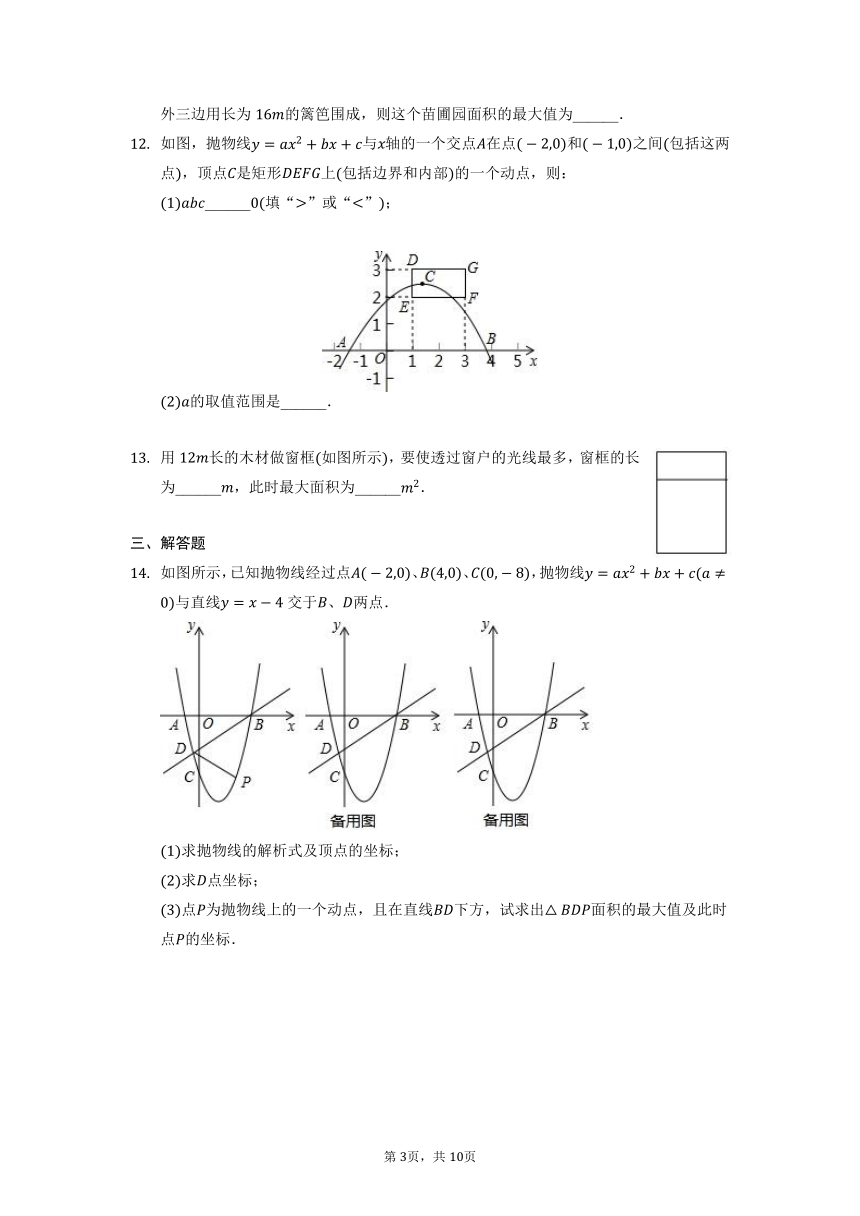
如图,抛物线与轴的一个交点在点和之间包括这两点,顶点是矩形上包括边界和内部的一个动点,则:
______填“”或“”;
的取值范围是______.
用长的木材做窗框如图所示,要使透过窗户的光线最多,窗框的长为______,此时最大面积为______.
三、解答题
如图所示,已知抛物线经过点、、,抛物线与直线交于、两点.
求抛物线的解析式及顶点的坐标;
求点坐标;
点为抛物线上的一个动点,且在直线下方,试求出面积的最大值及此时点的坐标.
答案和解析
1.【答案】
【解析】解:根据题意的横坐标为,
把代入,
得,
,,
即水面与桥拱顶的高度等于.
2.【答案】
【解答】
解:,,,,
,
的面积,
,
,
,
,
,
.
故选:.
3.【答案】
【解析】解:建立平面直角坐标系,设横轴通过,纵轴通过中点且通过点,则通过画图可得知为原点,
抛物线以轴为对称轴,且经过,两点,和可求出为的一半米,抛物线顶点坐标为,
设顶点式,把点坐标代入得,
抛物线解析式为,
当水面下降米,通过抛物线在图上的观察可转化为:
当时,对应的抛物线上两点之间的距离,也就是直线与抛物线相交的两点之间的距离,
可以通过把代入抛物线解析式得出:
,
解得:,
,
所以水面下降,水面宽度增加米.
4.【答案】
【解析】解:设平行于墙的一边长为,苗圃园面积为,则
有最大值,时,
墙长为
当时,最小
这个苗圃园面积的最大值和最小值分别为,.
5.【答案】
【解析】解:长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,
与之间的关系式是:.
故选:.
原长方形的边长减少后得到的新长方形的边长为,和,周长为,自变量的范围应能使长方形的边长是正数,即满足,.
6.【答案】
【解析】解:由图象可知,小球在空中达到的最大高度为,则小球在空中经过的路程一定大于,故错误;
由图象可知,小球时落地,故小球运动的时间为,故正确;
小球抛出秒时达到最高点,即速度为,故正确;
设函数解析式为,将代入得:
,
解得,
函数解析式为,
当时,,
正确.
综上,正确的有.
故选:.
可直接由函数图象中的信息分析得出答案;可由待定系数法求得函数解析式,再将代入计算,即可作出判断.
7.【答案】
【解析】解:如图,建立如图所示的平面直角坐标系,由题意可得,,,,
设大孔所在抛物线解析式为,
,
点,
,
,
大孔所在抛物线解析式为,
设点,
则设顶点为的小孔所在抛物线的解析式为,
,
点的横坐标为,
点坐标为,
,
,,
,
,
顶点为的小孔所在抛物线的解析式为,
大孔水面宽度为米,
当时,,
,
,,
单个小孔的水面宽度米,
8.【答案】
【解析】解:,
则当时,取得最大值,此时,
故飞机着陆后滑行到停下来滑行的距离为:.
故选:.
将,化为顶点式,即可求得的最大值,从而可以解答本题.
9.【答案】
【解析】解:,
顶点坐标为,
,
当时,有最大值,最大值为.
10.【答案】
【解析】解:建立平面直角坐标系如图:
则抛物线顶点坐标为,
设抛物线解析式,
将点坐标代入,可得:,
解得:,
故抛物线解析式为,
当水面下降米,通过抛物线在图上的观察可转化为:
当时,对应的抛物线上两点之间的距离,
也就是直线与抛物线相交的两点之间的距离,
将代入抛物线解析式得出:,
解得:,
所以水面宽度为米,
故水面宽度增加了米,
故答案为:.
建立平面直角坐标系,根据题意设出抛物线解析式,利用待定系数法求出解析式,根据题意计算即可.
11.【答案】
【解析】解:设垂直于墙面的长为,则平行于墙面的长为,由题意可知:
,且,
墙长为,
,
,
当时,取得最大值,最大值为;
故答案为:.
12.【答案】;
【解析】
解:观察图形发现,抛物线的开口向下,
,
顶点坐标在第一象限,
,
,
而抛物线与轴的交点在轴的上方,
,
;
故填
顶点是矩形上包括边界和内部的一个动点,
当顶点与点重合,顶点坐标为,则抛物线解析式,
由,解得;
当顶点与点重合,顶点坐标为,则抛物线解析式,
由,解得;
顶点可以在矩形内部,
.
解法二:由题意及图可知:当抛物线经过,顶点为时,抛物线开口最大,解得;
当抛物线经过,顶点为时,抛物线开口最小,解得,当时,越小抛物线的开口越小,越大抛物线的开口越大,故填
13.【答案】
【解析】解:设窗框的长为,则窗框的宽为,
所以,窗框的面积,
,
当时,窗框的面积最大,透过窗户的光线最多,此时最大面积为.
故答案为:,.
设窗框的长为,根据木材的总长度是表示出宽,然后根据窗框的面积列式整理,再根据二次函数的最值问题解答.
14.【答案】解:抛物线的表达式为:,
故,解得:,
故抛物线的表达式为:;
联立和,
得,
解得:或舍去,
故点;
过点作轴的平行线交于点,
设点,则点
面积,
,故面积有最大值为:;此时,,
即点
第2页,共2页
第1页,共1页
一、选择题
赵州桥的桥拱可以用抛物线的一部分表示,函数关系为,当水面宽度为时,水面与桥拱顶的高度等于
A.
B.
C.
D.
在中,,,,,若,则的面积关于边长的函数关系式为
A. B. C. D.
如图是抛物线形拱桥,当拱顶高离水面时,水面宽,水面下降,水面宽度增加
A.
B.
C.
D.
有一个矩形苗圃园,其中一边靠墙,另外边用长为的篱笆围成.已知墙长为,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为
A. ,
B. ,
C. ,
D. ,
长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,则与之间的关系式是
A. B.
C. D.
从地面竖直向上抛出一小球,小球的高度单位:与小球运动时间单位:之间的函数关系如图所示.下列结论:
小球在空中经过的路程是;
小球运动的时间为;
小球抛出秒时,速度为;
当时,小球的高度.
其中正确的是
A. B. C. D.
三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为米,孔顶离水面米;当水位下降,大孔水面宽度为米时,单个小孔的水面宽度为米,若大孔水面宽度为米,则单个小孔的水面宽度为
A. 米 B. 米 C. 米 D. 米
飞机着陆后滑行的距离米关于滑行的时间秒的函数解析式是,则飞机着陆后滑行到停止下来,滑行的距离为
A. 米 B. 米 C. 米 D. 米
一个运动员打高尔夫球,若球的飞行高度与水平距离之间的函数表达式为:,则高尔夫球在飞行过程中的最大高度为.
A. B. C. D.
二、填空
如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面米高时,水面为米,则当水面下降米时,水面宽度增加______米.
如图,有一个矩形苗圃园、其中一边靠墙墙长为,另外三边用长为的篱笆围成,则这个苗圃园面积的最大值为______.
如图,抛物线与轴的一个交点在点和之间包括这两点,顶点是矩形上包括边界和内部的一个动点,则:
______填“”或“”;
的取值范围是______.
用长的木材做窗框如图所示,要使透过窗户的光线最多,窗框的长为______,此时最大面积为______.
三、解答题
如图所示,已知抛物线经过点、、,抛物线与直线交于、两点.
求抛物线的解析式及顶点的坐标;
求点坐标;
点为抛物线上的一个动点,且在直线下方,试求出面积的最大值及此时点的坐标.
答案和解析
1.【答案】
【解析】解:根据题意的横坐标为,
把代入,
得,
,,
即水面与桥拱顶的高度等于.
2.【答案】
【解答】
解:,,,,
,
的面积,
,
,
,
,
,
.
故选:.
3.【答案】
【解析】解:建立平面直角坐标系,设横轴通过,纵轴通过中点且通过点,则通过画图可得知为原点,
抛物线以轴为对称轴,且经过,两点,和可求出为的一半米,抛物线顶点坐标为,
设顶点式,把点坐标代入得,
抛物线解析式为,
当水面下降米,通过抛物线在图上的观察可转化为:
当时,对应的抛物线上两点之间的距离,也就是直线与抛物线相交的两点之间的距离,
可以通过把代入抛物线解析式得出:
,
解得:,
,
所以水面下降,水面宽度增加米.
4.【答案】
【解析】解:设平行于墙的一边长为,苗圃园面积为,则
有最大值,时,
墙长为
当时,最小
这个苗圃园面积的最大值和最小值分别为,.
5.【答案】
【解析】解:长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,
与之间的关系式是:.
故选:.
原长方形的边长减少后得到的新长方形的边长为,和,周长为,自变量的范围应能使长方形的边长是正数,即满足,.
6.【答案】
【解析】解:由图象可知,小球在空中达到的最大高度为,则小球在空中经过的路程一定大于,故错误;
由图象可知,小球时落地,故小球运动的时间为,故正确;
小球抛出秒时达到最高点,即速度为,故正确;
设函数解析式为,将代入得:
,
解得,
函数解析式为,
当时,,
正确.
综上,正确的有.
故选:.
可直接由函数图象中的信息分析得出答案;可由待定系数法求得函数解析式,再将代入计算,即可作出判断.
7.【答案】
【解析】解:如图,建立如图所示的平面直角坐标系,由题意可得,,,,
设大孔所在抛物线解析式为,
,
点,
,
,
大孔所在抛物线解析式为,
设点,
则设顶点为的小孔所在抛物线的解析式为,
,
点的横坐标为,
点坐标为,
,
,,
,
,
顶点为的小孔所在抛物线的解析式为,
大孔水面宽度为米,
当时,,
,
,,
单个小孔的水面宽度米,
8.【答案】
【解析】解:,
则当时,取得最大值,此时,
故飞机着陆后滑行到停下来滑行的距离为:.
故选:.
将,化为顶点式,即可求得的最大值,从而可以解答本题.
9.【答案】
【解析】解:,
顶点坐标为,
,
当时,有最大值,最大值为.
10.【答案】
【解析】解:建立平面直角坐标系如图:
则抛物线顶点坐标为,
设抛物线解析式,
将点坐标代入,可得:,
解得:,
故抛物线解析式为,
当水面下降米,通过抛物线在图上的观察可转化为:
当时,对应的抛物线上两点之间的距离,
也就是直线与抛物线相交的两点之间的距离,
将代入抛物线解析式得出:,
解得:,
所以水面宽度为米,
故水面宽度增加了米,
故答案为:.
建立平面直角坐标系,根据题意设出抛物线解析式,利用待定系数法求出解析式,根据题意计算即可.
11.【答案】
【解析】解:设垂直于墙面的长为,则平行于墙面的长为,由题意可知:
,且,
墙长为,
,
,
当时,取得最大值,最大值为;
故答案为:.
12.【答案】;
【解析】
解:观察图形发现,抛物线的开口向下,
,
顶点坐标在第一象限,
,
,
而抛物线与轴的交点在轴的上方,
,
;
故填
顶点是矩形上包括边界和内部的一个动点,
当顶点与点重合,顶点坐标为,则抛物线解析式,
由,解得;
当顶点与点重合,顶点坐标为,则抛物线解析式,
由,解得;
顶点可以在矩形内部,
.
解法二:由题意及图可知:当抛物线经过,顶点为时,抛物线开口最大,解得;
当抛物线经过,顶点为时,抛物线开口最小,解得,当时,越小抛物线的开口越小,越大抛物线的开口越大,故填
13.【答案】
【解析】解:设窗框的长为,则窗框的宽为,
所以,窗框的面积,
,
当时,窗框的面积最大,透过窗户的光线最多,此时最大面积为.
故答案为:,.
设窗框的长为,根据木材的总长度是表示出宽,然后根据窗框的面积列式整理,再根据二次函数的最值问题解答.
14.【答案】解:抛物线的表达式为:,
故,解得:,
故抛物线的表达式为:;
联立和,
得,
解得:或舍去,
故点;
过点作轴的平行线交于点,
设点,则点
面积,
,故面积有最大值为:;此时,,
即点
第2页,共2页
第1页,共1页
