1.2.5 空间中的距离课时检测-2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册(含答案)
文档属性
| 名称 | 1.2.5 空间中的距离课时检测-2021-2022学年高二上学期数学人教B版(2019)选择性必修第一册(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 311.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 00:00:00 | ||
图片预览

文档简介
课时跟踪检测 空间中的距离
[A级]
1.已知平面α的一个法向量为n=(-2,-2,1),点A(-1,3,0)在平面α内,则点P(-2,1,4)到平面α的距离为( )
A.10 B.3
C. D.
2.如图所示,在长方体ABCD A1B1C1D1中,AB=BC=2,AA1=,E,F分别是平面A1B1C1D1,平面BCC1B1的中心,则E,F两点间的距离为( )
A.1 B.
C. D.
3.正方体ABCD A1B1C1D1的棱长为1,则点A到平面B1D1DB的距离为( )
A. B.2
C. D.
4.如图所示,在平行六面体ABCD A′B′C′D′中,AB=1,AD=2,AA′=3,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长为( )
A. B.
C. D.
5.已知正方体ABCD A1B1C1D1的棱长为2,点E是A1B1的中点,则点A到直线BE的距离是( )
A. B.
C. D.
6.已知平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱的棱长都等于2,且两两夹角都是60°,则A,C1两点间的距离是________.
7.已知棱长为1的正方体ABCD EFGH,若点P在正方体内部且满足=++,则点P到AB的距离为________.
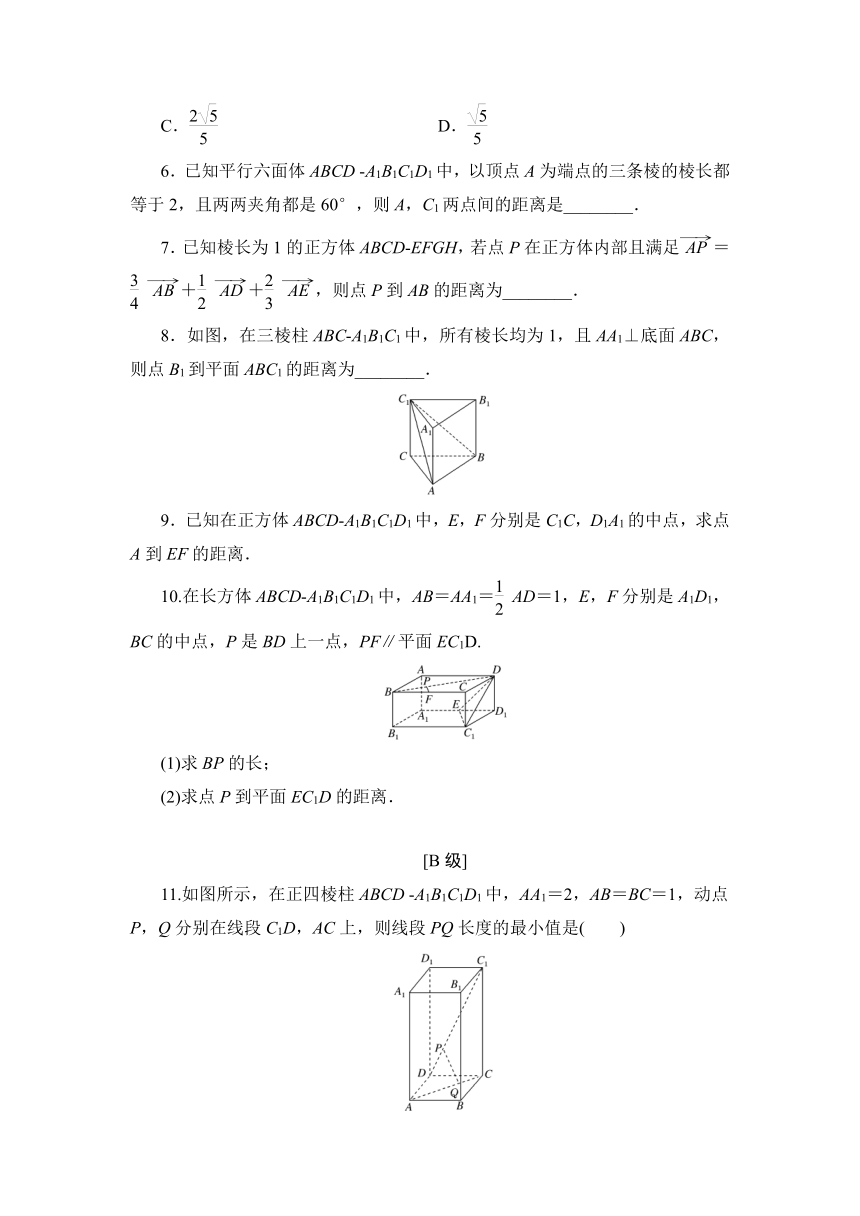
8.如图,在三棱柱ABC A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为________.
9.已知在正方体ABCD A1B1C1D1中,E,F分别是C1C,D1A1的中点,求点A到EF的距离.
10.在长方体ABCD A1B1C1D1中,AB=AA1=AD=1,E,F分别是A1D1,BC的中点,P是BD上一点,PF∥平面EC1D.
(1)求BP的长;
(2)求点P到平面EC1D的距离.
[B级]
11.如图所示,在正四棱柱ABCD A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( )
A. B.
C. D.
12.(多选)如图所示,在正三棱柱ABC A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF,则AF的长为( )
A.a B.a
C.2a D.2a
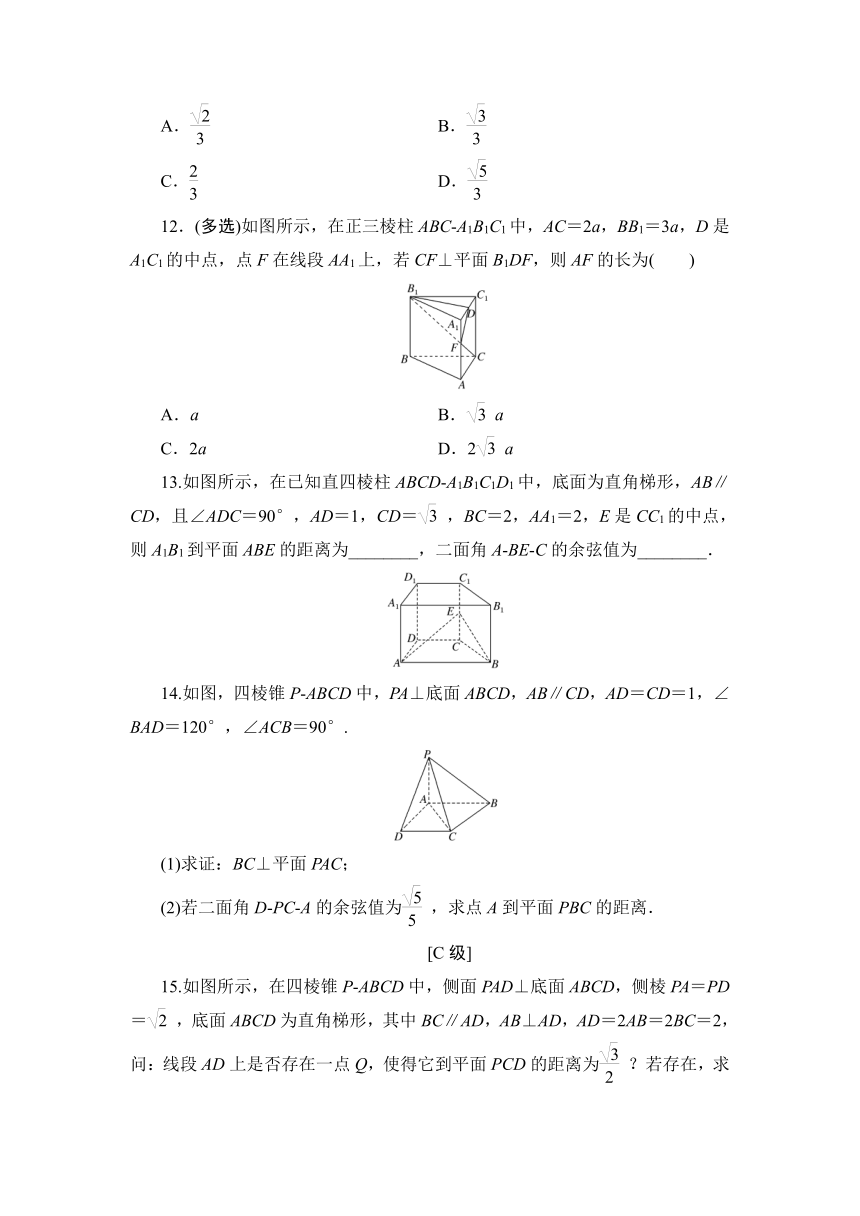
13.如图所示,在已知直四棱柱ABCD A1B1C1D1中,底面为直角梯形,AB∥CD,且∠ADC=90°,AD=1,CD=,BC=2,AA1=2,E是CC1的中点,则A1B1到平面ABE的距离为________,二面角A BE C的余弦值为________.
14.如图,四棱锥P ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°.
(1)求证:BC⊥平面PAC;
(2)若二面角D PC A的余弦值为,求点A到平面PBC的距离.
[C级]
15.如图所示,在四棱锥P ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,问:线段AD上是否存在一点Q,使得它到平面PCD的距离为?若存在,求出的值;若不存在,说明理由.
参考答案
1.D
2. C
3.C
4. B
5.B
6.2
7.
8.
9.解:以D点为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系如图所示,设DA=2,则A(2,0,0),E(0,2,1),F(1,0,2),则=(1,-2,1), =(1,0,-2).
||==,
·=1×1+0×(-2)+(-2)×1=-1,
在上的投影长为 eq \f(|·|,||) = .
所以点A到EF的距离
d=
==.
10.
解:(1)以A1为原点,A1B1,A1D1,A1A所在直线分别为x,y,z轴,建立空间直角坐标系,如图所示.
B(1,0,1),D(0,2,1),F(1,1,1),E(0,1,0),C1(1,2,0),
设P(a,b,1),=λ,λ∈[0,1],=(0,1,1),=(1,1,0),=(-1,2,0),
则=(a-1,b,0)=(-λ,2λ,0),
∴P(1-λ,2λ,1),=(λ,1-2λ,0),
设平面DEC1的法向量n=(x,y,z),
则 eq \b\lc\{(\a\vs4\al\co1(n·=y+z=0,,n·=x+y=0,)) 取x=1,得n=(1,-1,1),
∵PF∥平面EC1D,
∴·n=λ-1+2λ=0,
解得λ=,
∴P,
∴BP的长||==.
(2)由(1)得平面DEC1的法向量n=(1,-1,1),=,
∴点P到平面EC1D的距离:
d= eq \f(|·n|,|n|) ==.
11. C
12.AC
13.
14.
解:(1)证明:∵PA⊥底面ABCD,BC 平面ABCD,
∴PA⊥BC,
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,
∴BC⊥平面PAC.
(2)设AP=h,取CD的中点E,连接AE,则AE⊥CD,∴AE⊥AB.又PA⊥底面ABCD,∴PA⊥AE,PA⊥AB,故建立如图所示的空间直角坐标系,则A(0,0,0),P(0,0,h),C,
D,B(0,2,0),
=,=(0,1,0),
设平面PDC的法向量n1=(x1,y1,z1),
则 eq \b\lc\{(\a\vs4\al\co1(n1·=0,,n1·=0,)) 即
取x1=h,∴n1=.
由(1)知平面PAC的一个法向量为eq \o(,\s\up7(―→))=,
∴|cos 〈n1,eq \o(,\s\up7(―→))〉|==,
解得h=,
同理可求得平面PBC的一个法向量n2=(3,,2),
∴点A到平面PBC的距离为
d= eq \f(|·n2|,|n2|) ==.
15.
解:取AD的中点O,连接PO,OC.在△PAD中,∵PA=PD,∴PO⊥AD.
又侧面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD.
建立如图所示的空间直角坐标系,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),P(0,0,1),
则=(-1,0,1),=(-1,1,0).
假设存在点Q,使它到平面PCD的距离为,
设Q(0,y,0)(-1≤y≤1),则=(-1,y,0).
设平面PCD的法向量为n=(x0,y0,z0),
则 eq \b\lc\{(\a\vs4\al\co1(n·=0,,n·=0,)) ∴即x0=y0=z0,取x0=1,
则平面PCD的一个法向量为n=(1,1,1).
∴点Q到平面PCD的距离d= eq \f(|·n|,|n|) ==,
∴y=-或y=(舍去).此时=,=,则||=,||=.
∴存在点Q满足题意,此时=.
[A级]
1.已知平面α的一个法向量为n=(-2,-2,1),点A(-1,3,0)在平面α内,则点P(-2,1,4)到平面α的距离为( )
A.10 B.3
C. D.
2.如图所示,在长方体ABCD A1B1C1D1中,AB=BC=2,AA1=,E,F分别是平面A1B1C1D1,平面BCC1B1的中心,则E,F两点间的距离为( )
A.1 B.
C. D.
3.正方体ABCD A1B1C1D1的棱长为1,则点A到平面B1D1DB的距离为( )
A. B.2
C. D.
4.如图所示,在平行六面体ABCD A′B′C′D′中,AB=1,AD=2,AA′=3,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′的长为( )
A. B.
C. D.
5.已知正方体ABCD A1B1C1D1的棱长为2,点E是A1B1的中点,则点A到直线BE的距离是( )
A. B.
C. D.
6.已知平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱的棱长都等于2,且两两夹角都是60°,则A,C1两点间的距离是________.
7.已知棱长为1的正方体ABCD EFGH,若点P在正方体内部且满足=++,则点P到AB的距离为________.
8.如图,在三棱柱ABC A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为________.
9.已知在正方体ABCD A1B1C1D1中,E,F分别是C1C,D1A1的中点,求点A到EF的距离.
10.在长方体ABCD A1B1C1D1中,AB=AA1=AD=1,E,F分别是A1D1,BC的中点,P是BD上一点,PF∥平面EC1D.
(1)求BP的长;
(2)求点P到平面EC1D的距离.
[B级]
11.如图所示,在正四棱柱ABCD A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( )
A. B.
C. D.
12.(多选)如图所示,在正三棱柱ABC A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF,则AF的长为( )
A.a B.a
C.2a D.2a
13.如图所示,在已知直四棱柱ABCD A1B1C1D1中,底面为直角梯形,AB∥CD,且∠ADC=90°,AD=1,CD=,BC=2,AA1=2,E是CC1的中点,则A1B1到平面ABE的距离为________,二面角A BE C的余弦值为________.
14.如图,四棱锥P ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,∠ACB=90°.
(1)求证:BC⊥平面PAC;
(2)若二面角D PC A的余弦值为,求点A到平面PBC的距离.
[C级]
15.如图所示,在四棱锥P ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,问:线段AD上是否存在一点Q,使得它到平面PCD的距离为?若存在,求出的值;若不存在,说明理由.
参考答案
1.D
2. C
3.C
4. B
5.B
6.2
7.
8.
9.解:以D点为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系如图所示,设DA=2,则A(2,0,0),E(0,2,1),F(1,0,2),则=(1,-2,1), =(1,0,-2).
||==,
·=1×1+0×(-2)+(-2)×1=-1,
在上的投影长为 eq \f(|·|,||) = .
所以点A到EF的距离
d=
==.
10.
解:(1)以A1为原点,A1B1,A1D1,A1A所在直线分别为x,y,z轴,建立空间直角坐标系,如图所示.
B(1,0,1),D(0,2,1),F(1,1,1),E(0,1,0),C1(1,2,0),
设P(a,b,1),=λ,λ∈[0,1],=(0,1,1),=(1,1,0),=(-1,2,0),
则=(a-1,b,0)=(-λ,2λ,0),
∴P(1-λ,2λ,1),=(λ,1-2λ,0),
设平面DEC1的法向量n=(x,y,z),
则 eq \b\lc\{(\a\vs4\al\co1(n·=y+z=0,,n·=x+y=0,)) 取x=1,得n=(1,-1,1),
∵PF∥平面EC1D,
∴·n=λ-1+2λ=0,
解得λ=,
∴P,
∴BP的长||==.
(2)由(1)得平面DEC1的法向量n=(1,-1,1),=,
∴点P到平面EC1D的距离:
d= eq \f(|·n|,|n|) ==.
11. C
12.AC
13.
14.
解:(1)证明:∵PA⊥底面ABCD,BC 平面ABCD,
∴PA⊥BC,
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,
∴BC⊥平面PAC.
(2)设AP=h,取CD的中点E,连接AE,则AE⊥CD,∴AE⊥AB.又PA⊥底面ABCD,∴PA⊥AE,PA⊥AB,故建立如图所示的空间直角坐标系,则A(0,0,0),P(0,0,h),C,
D,B(0,2,0),
=,=(0,1,0),
设平面PDC的法向量n1=(x1,y1,z1),
则 eq \b\lc\{(\a\vs4\al\co1(n1·=0,,n1·=0,)) 即
取x1=h,∴n1=.
由(1)知平面PAC的一个法向量为eq \o(,\s\up7(―→))=,
∴|cos 〈n1,eq \o(,\s\up7(―→))〉|==,
解得h=,
同理可求得平面PBC的一个法向量n2=(3,,2),
∴点A到平面PBC的距离为
d= eq \f(|·n2|,|n2|) ==.
15.
解:取AD的中点O,连接PO,OC.在△PAD中,∵PA=PD,∴PO⊥AD.
又侧面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD.
建立如图所示的空间直角坐标系,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),P(0,0,1),
则=(-1,0,1),=(-1,1,0).
假设存在点Q,使它到平面PCD的距离为,
设Q(0,y,0)(-1≤y≤1),则=(-1,y,0).
设平面PCD的法向量为n=(x0,y0,z0),
则 eq \b\lc\{(\a\vs4\al\co1(n·=0,,n·=0,)) ∴即x0=y0=z0,取x0=1,
则平面PCD的一个法向量为n=(1,1,1).
∴点Q到平面PCD的距离d= eq \f(|·n|,|n|) ==,
∴y=-或y=(舍去).此时=,=,则||=,||=.
∴存在点Q满足题意,此时=.
