3.3.1 抛物线及其标准方程 课时练习-2021-2022学年高二上学期数学 人教A版(2019)选择性必修第一册(含答案)
文档属性
| 名称 | 3.3.1 抛物线及其标准方程 课时练习-2021-2022学年高二上学期数学 人教A版(2019)选择性必修第一册(含答案) | 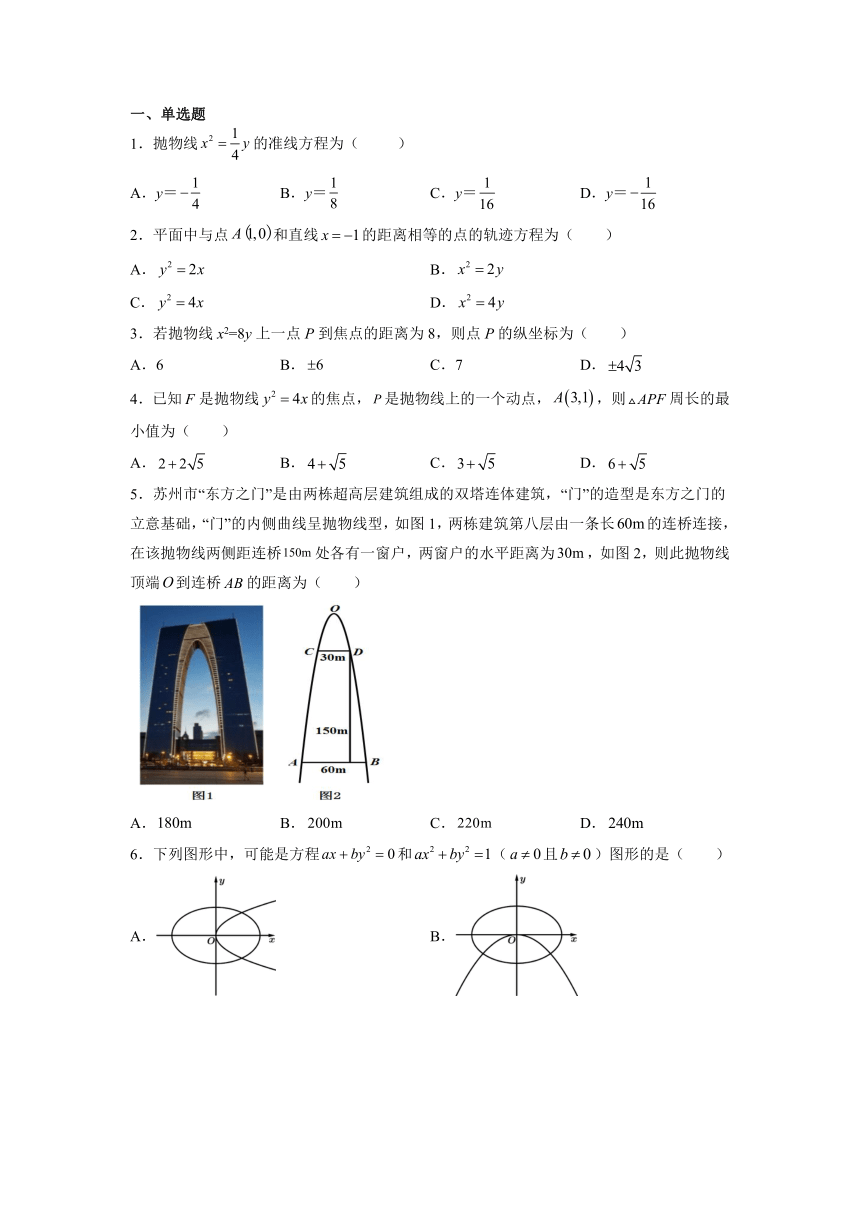 | |
| 格式 | docx | ||
| 文件大小 | 784.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 11:00:14 | ||
图片预览





文档简介
一、单选题
1.抛物线的准线方程为( )
A.y= B.y= C.y= D.y=
2.平面中与点和直线的距离相等的点的轨迹方程为( )
A. B.
C. D.
3.若抛物线x2=8y上一点P到焦点的距离为8,则点P的纵坐标为( )
A.6 B. C.7 D.
4.已知是抛物线的焦点,是抛物线上的一个动点,,则周长的最小值为( )
A. B. C. D.
5.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长的连桥连接,在该抛物线两侧距连桥处各有一窗户,两窗户的水平距离为,如图2,则此抛物线顶端到连桥的距离为( )
A. B. C. D.
6.下列图形中,可能是方程和(且)图形的是( )
A. B.
C. D.
7.抛物线上任意两点,处的切线交于点,称为“阿基米德三角形”,当线段经过抛物线的焦点时,具有以下特征:
①点必在抛物线的准线上;②.
若经过抛物线的焦点的一条弦为,“阿基米德三角形”为,且点的纵坐标为4,则直线的方程为( )
A. B.
C. D.
8.点到点、及到直线的距离都相等,如果这样的点恰好只有一个,则实数的值为( )
A. B. C. D.
二、多选题
9.下列四个抛物线中,焦点到准线的距离为1的是( )
A. B. C. D.
10.(多选)已知双曲线的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则( )
A.双曲线C1的渐近线为
B.双曲线C1的渐近线为
C.抛物线C2的方程为x2=8y
D.抛物线C2的方程为x2=16y
11.已知曲线,则下列说法正确的是( ).
A.若,,则曲线是椭圆
B.若,则曲线是焦点在轴上的椭圆
C.若,则曲线是焦点在轴上的双曲线
D.曲线可以是抛物线
12.已知圆的半径为定长,是圆所在平面内一个定点,是圆上任意一点,线段的垂直平分线和直线相交于点.当点在圆上运动时,下列判断正确的是( )
A.当点在圆内(不与圆心重合)时,点的轨迹是椭圆;
B.点的轨迹可能是一个定点;
C.点的轨迹可能是抛物线.
D.当点在圆外时,点的轨迹是双曲线的一支
三、填空题
13.若抛物线的焦点坐标为,则____;准线方程为_____.
14.抛物线上一点M的横坐标为3,且,则抛物线方程为_________.
15.某学习小组研究一种卫星接收天线(如图①所示),发现其曲面与轴截面的交线为抛物线,在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚焦到焦点处(如图②所示),已知接收天线的口径(直径)为,深度为,则该抛物线的焦点到顶点的距离为_______.
16.一个动圆与定圆相外切,且与直线相切,则动圆圆心的轨迹方程为_______.
四、解答题
17.分别求满足下列条件的抛物线的标准方程.
(1)过点(3,-4);
(2)焦点在直线x+3y+15=0上.
18.已知定点,曲线上的任一点都有.求曲线的方程.
19.已知椭圆的左 右焦点分别为,,抛物线与椭圆在第一象限的交点为Q,若.
(1)求三角形的面积;
(2)求此抛物线方程.
参考答案
1.D
2.C
3.A
4.B
抛物线的焦点,准线的方程为,过做,垂足为,
设周长为,
,由抛物线的定义可知:
,因此,当在同一条直线上时,有最小值,即
时,,
故选:B
5.B
建系如图,设抛物线方程为:,
由题意设,,
则,
解得:,.
所以此拋物线顶端到连桥的距离为:.
故选:B.
6.D
解:对A,方程表示椭圆,则,,则,抛物线方程应开口向左,故A错误;
对B,方程化为标准方程为,则抛物线的焦点在轴上,故B错误;
对C,方程表示焦点在轴上的双曲线,则,,则,则抛物线方程应开口向右,故C错误;
对D,方程表示焦点在轴上的双曲线,则,,则,则抛物线方程应开口向右,故D正确.
故选:D.
7.A
设抛物线的焦点为,
由题意可知,抛物线的焦点坐标为,准线方程为,
因为为“阿基米德三角形”,且线段经过抛物线的焦点,
所以点必在抛物线的准线上,
所以点,
直线的斜率为.
又因为,
所以直线的斜率为,
所以直线的方程为,即,
故选:A.
8.D
因为点在点的距离等于它到直线的距离,则点所在的曲线是以点为焦点,以直线为准线的抛物线,
设点,由已知可得,
所以,,(*)
①当时,方程(*)为,解得,符合题意;
②当时,则.
由①②可知,.
故选:D.
9.ACD
由题意知,,故A,D正确,B错误,
又,化简得,其图象与形状相同,
所以C正确.
故选:ACD.
10.AD
解析:因为的离心率为2,所以,即,所以,.
的焦点坐标为,的渐近线方程为,即,由题意得,所以.
故C2的方程为.
故选:AD
11.BC
对于A.若,且,则曲线是椭圆;若,则是圆.故A错误;
对于B.在时可化为,∵∴,所以曲线是焦点在轴上的椭圆.故B正确;
对于C.可化为,∵,∴,∴曲线是焦点在轴上的双曲线;
对于D. 曲线都不能化成抛物线的标准方程的形式,所以曲线不能是抛物线.
12.ABD
解:对A,如图1,连接,
由已知得.
所以.
又因为点在圆内,所以,
根据椭圆的定义,点的轨迹是以,为焦点,为长轴长的椭圆.
对B,如图2,
当点在圆上时,点与圆心重合,轨迹为定点;
对C,由于当点与圆心重合时,点的轨迹为圆,综合,,可知点的轨迹不可能为抛物线.
对D,如图3,连接,
由已知得.
所以.
又因为点在圆外,所以,
根据双曲线的定义,点的轨迹是以,为焦点,为实轴长的双曲线.
故选:ABD.
13.2,
14.
15.
如图所示,在接收天线的轴截面所在平面建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合,焦点在轴上,
设抛物线的标准方程为,由已知条件可得,点在抛物线上,
所以,,解得,
所以,所求抛物线的标准方程为,焦点坐标为,
因此,该抛物线的焦点到顶点的距离为.
故答案为:.
16.
由题意可知,圆的圆心为,半径为,
由于动圆与定圆相外切,且与直线相切,
动圆圆心到点的距离比它到直线的距离大,
所以,动圆圆心到点的距离等于它到直线的距离,
所以,动圆圆心的轨迹是以点为圆心,以直线为准线的抛物线,
设动圆圆心的轨迹方程为,则,可得,
所以,动圆圆心的轨迹方程为.
故答案为:.
17.(1)或;(2)或.
(1)∵点(3,-4)在第四象限,
∴抛物线开口向右或向下,设抛物线的标准方程为 (p>0)或 (p1>0).
将(3,-4)的坐标分别代入方程中,
∴由,得:;由,得.
∴所求抛物线的标准方程为或.
(2)令x=0得y=-5;令y=0得x=-15.
∴抛物线的焦点为(0,-5)或(-15,0).
∴所求抛物线的标准方程为或.
18.
解:设,由,得,
,
,化简整理得.
19.(1);(2).
解:(1)椭圆即,
,设,
则,
即,
所以三角形的面积为.
(2)设,在第一象限,
,
,所以,
代入抛物线方程得,
所以抛物线方程为.
1.抛物线的准线方程为( )
A.y= B.y= C.y= D.y=
2.平面中与点和直线的距离相等的点的轨迹方程为( )
A. B.
C. D.
3.若抛物线x2=8y上一点P到焦点的距离为8,则点P的纵坐标为( )
A.6 B. C.7 D.
4.已知是抛物线的焦点,是抛物线上的一个动点,,则周长的最小值为( )
A. B. C. D.
5.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长的连桥连接,在该抛物线两侧距连桥处各有一窗户,两窗户的水平距离为,如图2,则此抛物线顶端到连桥的距离为( )
A. B. C. D.
6.下列图形中,可能是方程和(且)图形的是( )
A. B.
C. D.
7.抛物线上任意两点,处的切线交于点,称为“阿基米德三角形”,当线段经过抛物线的焦点时,具有以下特征:
①点必在抛物线的准线上;②.
若经过抛物线的焦点的一条弦为,“阿基米德三角形”为,且点的纵坐标为4,则直线的方程为( )
A. B.
C. D.
8.点到点、及到直线的距离都相等,如果这样的点恰好只有一个,则实数的值为( )
A. B. C. D.
二、多选题
9.下列四个抛物线中,焦点到准线的距离为1的是( )
A. B. C. D.
10.(多选)已知双曲线的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则( )
A.双曲线C1的渐近线为
B.双曲线C1的渐近线为
C.抛物线C2的方程为x2=8y
D.抛物线C2的方程为x2=16y
11.已知曲线,则下列说法正确的是( ).
A.若,,则曲线是椭圆
B.若,则曲线是焦点在轴上的椭圆
C.若,则曲线是焦点在轴上的双曲线
D.曲线可以是抛物线
12.已知圆的半径为定长,是圆所在平面内一个定点,是圆上任意一点,线段的垂直平分线和直线相交于点.当点在圆上运动时,下列判断正确的是( )
A.当点在圆内(不与圆心重合)时,点的轨迹是椭圆;
B.点的轨迹可能是一个定点;
C.点的轨迹可能是抛物线.
D.当点在圆外时,点的轨迹是双曲线的一支
三、填空题
13.若抛物线的焦点坐标为,则____;准线方程为_____.
14.抛物线上一点M的横坐标为3,且,则抛物线方程为_________.
15.某学习小组研究一种卫星接收天线(如图①所示),发现其曲面与轴截面的交线为抛物线,在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚焦到焦点处(如图②所示),已知接收天线的口径(直径)为,深度为,则该抛物线的焦点到顶点的距离为_______.
16.一个动圆与定圆相外切,且与直线相切,则动圆圆心的轨迹方程为_______.
四、解答题
17.分别求满足下列条件的抛物线的标准方程.
(1)过点(3,-4);
(2)焦点在直线x+3y+15=0上.
18.已知定点,曲线上的任一点都有.求曲线的方程.
19.已知椭圆的左 右焦点分别为,,抛物线与椭圆在第一象限的交点为Q,若.
(1)求三角形的面积;
(2)求此抛物线方程.
参考答案
1.D
2.C
3.A
4.B
抛物线的焦点,准线的方程为,过做,垂足为,
设周长为,
,由抛物线的定义可知:
,因此,当在同一条直线上时,有最小值,即
时,,
故选:B
5.B
建系如图,设抛物线方程为:,
由题意设,,
则,
解得:,.
所以此拋物线顶端到连桥的距离为:.
故选:B.
6.D
解:对A,方程表示椭圆,则,,则,抛物线方程应开口向左,故A错误;
对B,方程化为标准方程为,则抛物线的焦点在轴上,故B错误;
对C,方程表示焦点在轴上的双曲线,则,,则,则抛物线方程应开口向右,故C错误;
对D,方程表示焦点在轴上的双曲线,则,,则,则抛物线方程应开口向右,故D正确.
故选:D.
7.A
设抛物线的焦点为,
由题意可知,抛物线的焦点坐标为,准线方程为,
因为为“阿基米德三角形”,且线段经过抛物线的焦点,
所以点必在抛物线的准线上,
所以点,
直线的斜率为.
又因为,
所以直线的斜率为,
所以直线的方程为,即,
故选:A.
8.D
因为点在点的距离等于它到直线的距离,则点所在的曲线是以点为焦点,以直线为准线的抛物线,
设点,由已知可得,
所以,,(*)
①当时,方程(*)为,解得,符合题意;
②当时,则.
由①②可知,.
故选:D.
9.ACD
由题意知,,故A,D正确,B错误,
又,化简得,其图象与形状相同,
所以C正确.
故选:ACD.
10.AD
解析:因为的离心率为2,所以,即,所以,.
的焦点坐标为,的渐近线方程为,即,由题意得,所以.
故C2的方程为.
故选:AD
11.BC
对于A.若,且,则曲线是椭圆;若,则是圆.故A错误;
对于B.在时可化为,∵∴,所以曲线是焦点在轴上的椭圆.故B正确;
对于C.可化为,∵,∴,∴曲线是焦点在轴上的双曲线;
对于D. 曲线都不能化成抛物线的标准方程的形式,所以曲线不能是抛物线.
12.ABD
解:对A,如图1,连接,
由已知得.
所以.
又因为点在圆内,所以,
根据椭圆的定义,点的轨迹是以,为焦点,为长轴长的椭圆.
对B,如图2,
当点在圆上时,点与圆心重合,轨迹为定点;
对C,由于当点与圆心重合时,点的轨迹为圆,综合,,可知点的轨迹不可能为抛物线.
对D,如图3,连接,
由已知得.
所以.
又因为点在圆外,所以,
根据双曲线的定义,点的轨迹是以,为焦点,为实轴长的双曲线.
故选:ABD.
13.2,
14.
15.
如图所示,在接收天线的轴截面所在平面建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合,焦点在轴上,
设抛物线的标准方程为,由已知条件可得,点在抛物线上,
所以,,解得,
所以,所求抛物线的标准方程为,焦点坐标为,
因此,该抛物线的焦点到顶点的距离为.
故答案为:.
16.
由题意可知,圆的圆心为,半径为,
由于动圆与定圆相外切,且与直线相切,
动圆圆心到点的距离比它到直线的距离大,
所以,动圆圆心到点的距离等于它到直线的距离,
所以,动圆圆心的轨迹是以点为圆心,以直线为准线的抛物线,
设动圆圆心的轨迹方程为,则,可得,
所以,动圆圆心的轨迹方程为.
故答案为:.
17.(1)或;(2)或.
(1)∵点(3,-4)在第四象限,
∴抛物线开口向右或向下,设抛物线的标准方程为 (p>0)或 (p1>0).
将(3,-4)的坐标分别代入方程中,
∴由,得:;由,得.
∴所求抛物线的标准方程为或.
(2)令x=0得y=-5;令y=0得x=-15.
∴抛物线的焦点为(0,-5)或(-15,0).
∴所求抛物线的标准方程为或.
18.
解:设,由,得,
,
,化简整理得.
19.(1);(2).
解:(1)椭圆即,
,设,
则,
即,
所以三角形的面积为.
(2)设,在第一象限,
,
,所以,
代入抛物线方程得,
所以抛物线方程为.
