2012-2013学年度保定美术中学第一学期高三第一次九月考数学试卷理科含答案
文档属性
| 名称 | 2012-2013学年度保定美术中学第一学期高三第一次九月考数学试卷理科含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-27 00:00:00 | ||
图片预览



文档简介
2012-2013学年度美术中学第一学期高三第一次月考
数 学 试 卷(理科)
第Ⅰ卷(选择题60分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则 ( )
A . B. C. D.
2.若,,,,则( )
A. B. C. D.
3.已知,向量与垂直,则实数的值为( )
A. B. C. D.
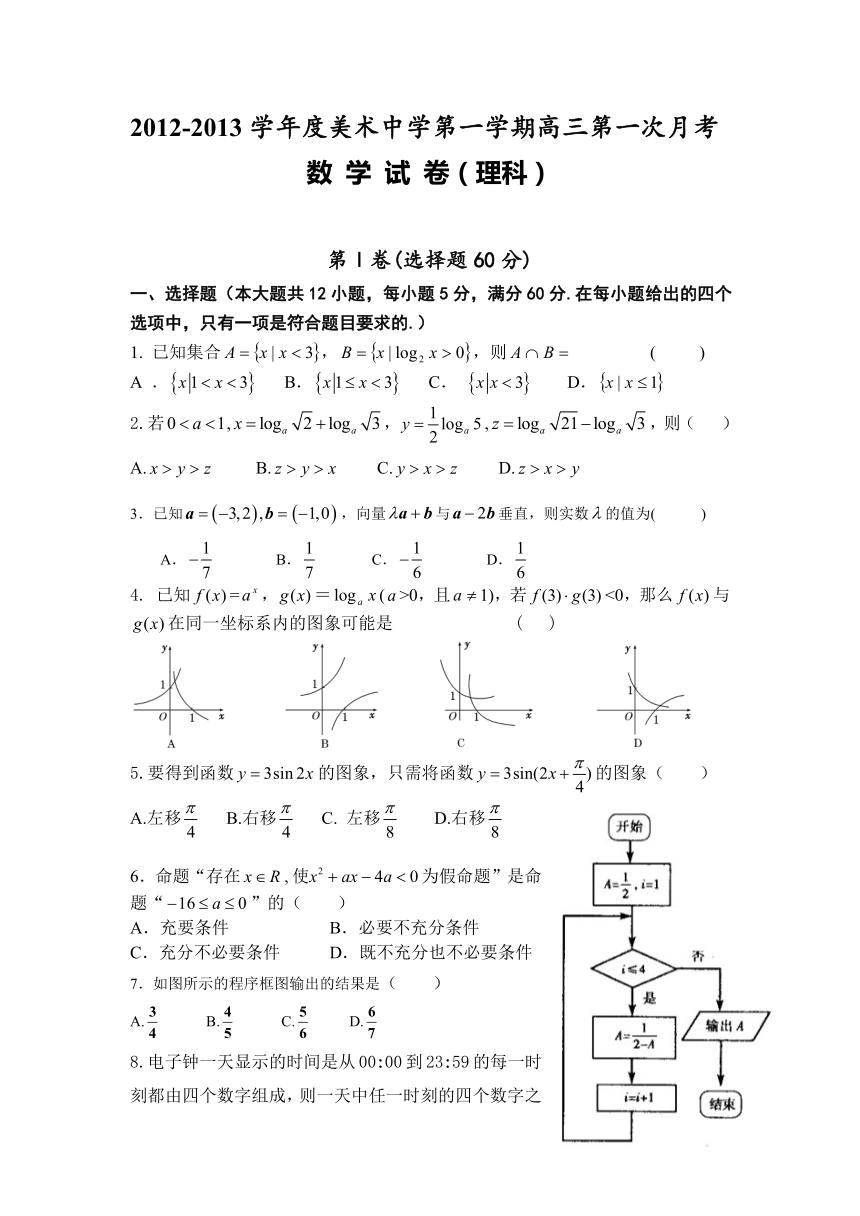
4. 已知=,=(>0,且1),若<0,那么与在同一坐标系内的图象可能是 ( )
5.要得到函数的图象,只需将函数的图象( )
A.左移 B.右移 C. 左移 D.右移
6.命题“存在为假命题”是命题“”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
7.如图所示的程序框图输出的结果是( )
A. B. C. D.
8.电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为23的概率为( )
A. B. C. D.
9.曲线y=+1在点(0,2)处的切线与直线y=0和y=x围成的三角形面积为( ) A. B. C. D.1
10.设为等差数列的前n项和,若,公差d = 2, ,则k = ( ) A. 8 B. 7 C. 6 D. 5
11.函数在区间上的最大值是( )
A.1 B. C. D.1+
12.已知函数若a,b,c互不相等,且,则的取值范围是( ) A. B. C. D.
第Ⅱ卷(非选择题90分)
二、填空题(每小题5分,共4小题,总分20分)
13.是周期为2的奇函数,当0≤x≤1时,=,则=_____
14.正四棱锥的侧棱长为,侧棱与底面所成的角为,则该棱锥的体积为__________.
15.已知,变量,满足约束条件,则的最大z值为__________.
16.下列说法正确的序号是: .
①命题“若,则x=1”的逆否命题为:“若x≠1,则”;②“x>1”是“|x|>1”的充分不必要条件;③若p且q为假命题,则p、q均为假命题;④命题:“,使得”,则:“,均有 ”
三、解答题(共6小题,总分70分)
17.(本小题满分10分)选修4-5:设函数,其中.
(I)当a=1时,求不等式的解集.
(II)若不等式的解集为{x|,求a的值.
18.(本小题满分12分)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体.()求该总体的平均数及方差(精确到0.01);(II)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
19.(本小题满分12分)在△ABC中,A、B为锐角,角A、B、C所对的边分
别为、、,且,.
(1)求角C的值; (2)若a-b=-1,求、、的值.
20.(本小题满分12分)已知是首项为19,公差为-2的等差数列,为的前项和.(Ⅰ)求通项及;(Ⅱ)设是首项为1,公比为3的等比数列,求数列的通项公式及其前项和.
21.(本小题满分12分)如图四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点.
(1)求证: (2)若求二面角的大小.
(3)在(2)的条件下,侧棱上是否存在一点,使得∥平面,若存在,求的值,若不存在,说明理由.
22. (本小题满分12分)已,且函数在处取得极值.(I)求的解析式与单调区间;
(II)是否存在实数,对任意的,都存在,使得成立?若存在,求出实数的取值范围;若不存在,说明理由
2012-2013学年度第一学期高三第一次月考
数 学 试 卷(理科答案)
一、选择题:本大题共12小题,每小题5分,共60分。
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C A C D A C C A D C C
二、填空题:本大题共6小题,每小题4分,共20分。
13、 14、
15、 5 16、 ① ② ④
三、解答题(共6小题,总分70分)
17.解:(Ⅰ)当时,可化为。
由此可得 或。故不等式的解集为或。
(Ⅱ) 由 得
此不等式化为不等式组
或即 或
因为,所以不等式组的解集为
由题设可得= ,故
18.(1)总体平均数为
(2)设A表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”从总体中抽取2个个体全部可能的基本结果有:(5,6), (5,7), (5,8), (5,9), (5,10), (6,7), (6,8), (6,9), (6,10), (7,8), (7,9), (7,10), (8,9), (8,10), (9,10),共15个基本结果。事件A包含的基本结果有:(5,9), (5,10), (6,8), (6,9), (6,10), (7,8), (7,9),共有7个基本结果;所以所求的概率为
∵A、B为锐角,sinA=,sinB=,
∴cosA==,------1分 cosB==,--------------2分
∴cosC=-cos(A+B)=-(cosAcosB-sinAsinB)=-(×-×)=.---------------5分 ∵0(2)由(1)知C=,∴sinC=. --------7分
由正弦定理==得a=b=c,即a=b,c=b,
∵a-b=-1,∴b-b=-1,∴b=1,∴a=,c=. ------12分
20.
21.解法一:(Ⅰ)连BD,设AC交BD于O,由题意。在正方形ABCD中,,所以,得.
(Ⅱ)设正方形边长,则。又,所以,
连,由(Ⅰ)知,所以,
且,所以是二面角的平面角。
由,知,所以,即二面角的大小为。
(Ⅲ)在棱SC上存在一点E,使
由(Ⅱ)可得,故可在上取一点,使,过作的平行线与的交点即为。连BN。在中知,又由于,故平面,得,由于,故.
22. (本小题满分14分)
(1) 解:,得,
且,,则 ………4分
; 递减区间为 ……7分
(II)由(1)得
x -1 2
+ 0 - 0 +
增 减 增
所以当时,, ……10分
假设对任意的都存在使得成立,
设的最大值为T,最小值为t,则,
又,所以当时
,
且, .
综上, ………14分
数 学 试 卷(理科)
第Ⅰ卷(选择题60分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则 ( )
A . B. C. D.
2.若,,,,则( )
A. B. C. D.
3.已知,向量与垂直,则实数的值为( )
A. B. C. D.
4. 已知=,=(>0,且1),若<0,那么与在同一坐标系内的图象可能是 ( )
5.要得到函数的图象,只需将函数的图象( )
A.左移 B.右移 C. 左移 D.右移
6.命题“存在为假命题”是命题“”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
7.如图所示的程序框图输出的结果是( )
A. B. C. D.
8.电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为23的概率为( )
A. B. C. D.
9.曲线y=+1在点(0,2)处的切线与直线y=0和y=x围成的三角形面积为( ) A. B. C. D.1
10.设为等差数列的前n项和,若,公差d = 2, ,则k = ( ) A. 8 B. 7 C. 6 D. 5
11.函数在区间上的最大值是( )
A.1 B. C. D.1+
12.已知函数若a,b,c互不相等,且,则的取值范围是( ) A. B. C. D.
第Ⅱ卷(非选择题90分)
二、填空题(每小题5分,共4小题,总分20分)
13.是周期为2的奇函数,当0≤x≤1时,=,则=_____
14.正四棱锥的侧棱长为,侧棱与底面所成的角为,则该棱锥的体积为__________.
15.已知,变量,满足约束条件,则的最大z值为__________.
16.下列说法正确的序号是: .
①命题“若,则x=1”的逆否命题为:“若x≠1,则”;②“x>1”是“|x|>1”的充分不必要条件;③若p且q为假命题,则p、q均为假命题;④命题:“,使得”,则:“,均有 ”
三、解答题(共6小题,总分70分)
17.(本小题满分10分)选修4-5:设函数,其中.
(I)当a=1时,求不等式的解集.
(II)若不等式的解集为{x|,求a的值.
18.(本小题满分12分)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体.()求该总体的平均数及方差(精确到0.01);(II)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
19.(本小题满分12分)在△ABC中,A、B为锐角,角A、B、C所对的边分
别为、、,且,.
(1)求角C的值; (2)若a-b=-1,求、、的值.
20.(本小题满分12分)已知是首项为19,公差为-2的等差数列,为的前项和.(Ⅰ)求通项及;(Ⅱ)设是首项为1,公比为3的等比数列,求数列的通项公式及其前项和.
21.(本小题满分12分)如图四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点.
(1)求证: (2)若求二面角的大小.
(3)在(2)的条件下,侧棱上是否存在一点,使得∥平面,若存在,求的值,若不存在,说明理由.
22. (本小题满分12分)已,且函数在处取得极值.(I)求的解析式与单调区间;
(II)是否存在实数,对任意的,都存在,使得成立?若存在,求出实数的取值范围;若不存在,说明理由
2012-2013学年度第一学期高三第一次月考
数 学 试 卷(理科答案)
一、选择题:本大题共12小题,每小题5分,共60分。
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C A C D A C C A D C C
二、填空题:本大题共6小题,每小题4分,共20分。
13、 14、
15、 5 16、 ① ② ④
三、解答题(共6小题,总分70分)
17.解:(Ⅰ)当时,可化为。
由此可得 或。故不等式的解集为或。
(Ⅱ) 由 得
此不等式化为不等式组
或即 或
因为,所以不等式组的解集为
由题设可得= ,故
18.(1)总体平均数为
(2)设A表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”从总体中抽取2个个体全部可能的基本结果有:(5,6), (5,7), (5,8), (5,9), (5,10), (6,7), (6,8), (6,9), (6,10), (7,8), (7,9), (7,10), (8,9), (8,10), (9,10),共15个基本结果。事件A包含的基本结果有:(5,9), (5,10), (6,8), (6,9), (6,10), (7,8), (7,9),共有7个基本结果;所以所求的概率为
∵A、B为锐角,sinA=,sinB=,
∴cosA==,------1分 cosB==,--------------2分
∴cosC=-cos(A+B)=-(cosAcosB-sinAsinB)=-(×-×)=.---------------5分 ∵0
由正弦定理==得a=b=c,即a=b,c=b,
∵a-b=-1,∴b-b=-1,∴b=1,∴a=,c=. ------12分
20.
21.解法一:(Ⅰ)连BD,设AC交BD于O,由题意。在正方形ABCD中,,所以,得.
(Ⅱ)设正方形边长,则。又,所以,
连,由(Ⅰ)知,所以,
且,所以是二面角的平面角。
由,知,所以,即二面角的大小为。
(Ⅲ)在棱SC上存在一点E,使
由(Ⅱ)可得,故可在上取一点,使,过作的平行线与的交点即为。连BN。在中知,又由于,故平面,得,由于,故.
22. (本小题满分14分)
(1) 解:,得,
且,,则 ………4分
; 递减区间为 ……7分
(II)由(1)得
x -1 2
+ 0 - 0 +
增 减 增
所以当时,, ……10分
假设对任意的都存在使得成立,
设的最大值为T,最小值为t,则,
又,所以当时
,
且, .
综上, ………14分
同课章节目录
