北师大版八年级数学上册 1.1 探索勾股定理课件(共28张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 1.1 探索勾股定理课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 17:50:40 | ||
图片预览



文档简介
(共28张PPT)
1 探索勾股定理
第一章 勾股定理
观察:图中两个正方形是怎样形成的,你知道它有什么意义吗?
这是1955年希腊为纪念一个数学学派发行的邮票.
观察:发现下面邮票中三个正方形的面积关系
1.经历探索勾股定理及验证勾股定理的过程,了解勾股定理的探究方法及其内在联系.
2.掌握勾股定理,并能运用勾股定理解决一些实际问题.
P
R
Q
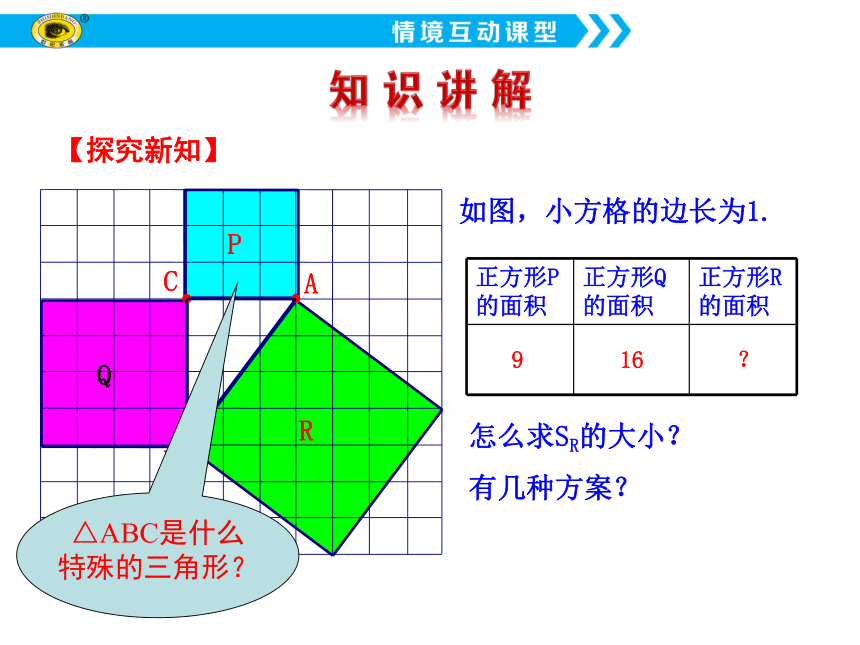
正方形P的面积 正方形Q的面积 正方形R的面积
A
B
C
9
16
?
怎么求SR的大小?
有几种方案?
如图,小方格的边长为1.
【探究新知】
△ABC是什么特殊的三角形?
P
Q
C
R
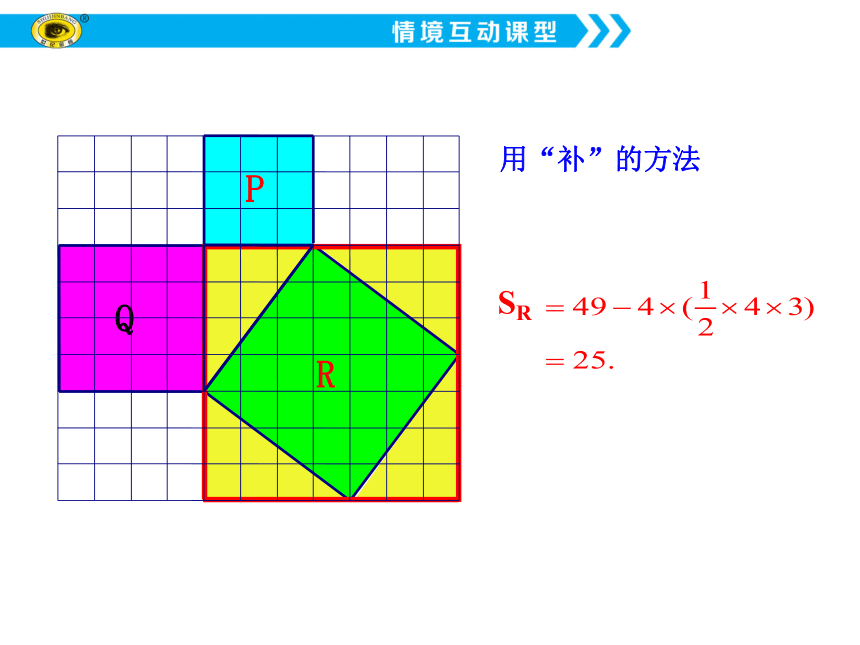
用“补”的方法
SR
P
Q
C
R
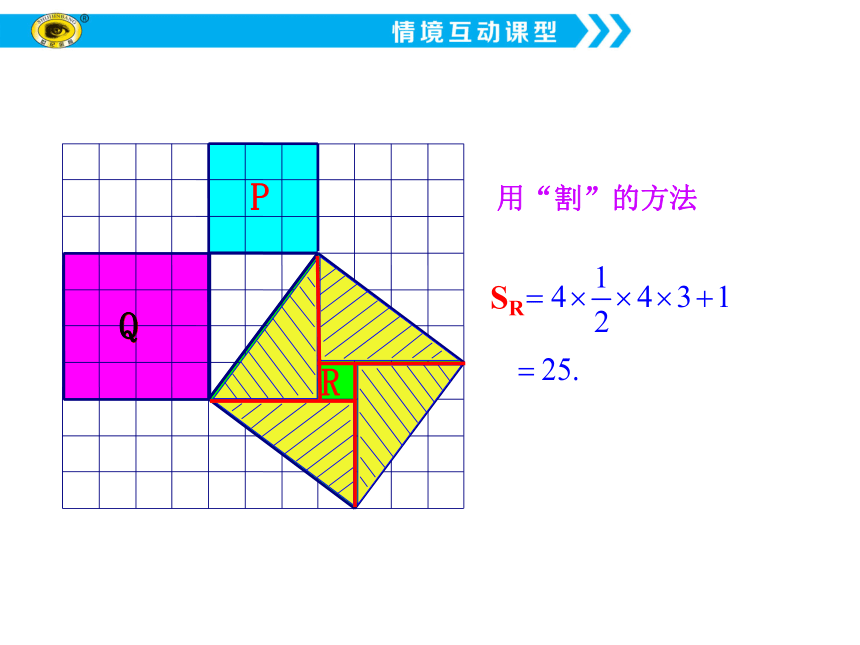
用“割”的方法
Q
SR
A
B
C
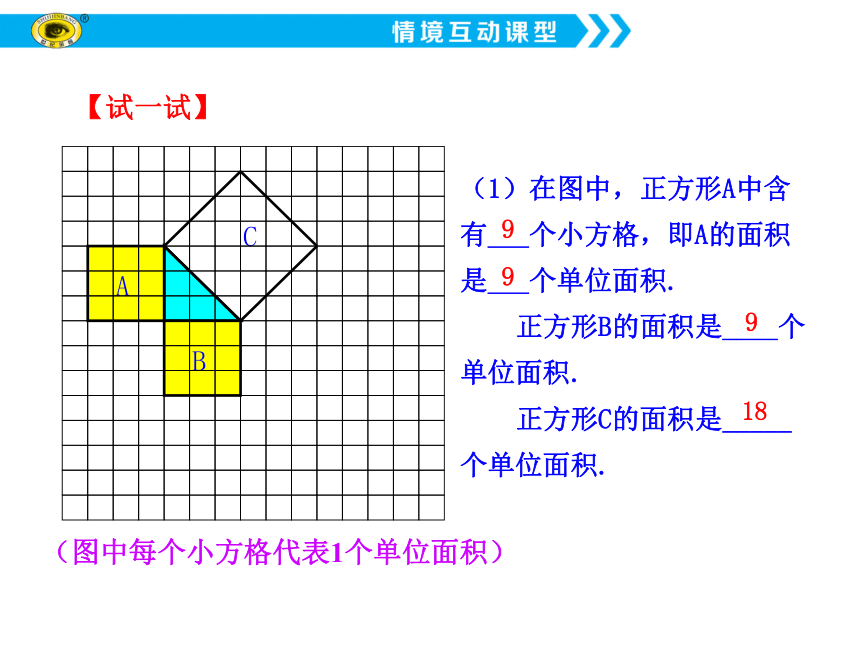
(图中每个小方格代表1个单位面积)
(1)在图中,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是____个
单位面积.
正方形C的面积是_____
个单位面积.
9
9
9
18
【试一试】
A
B
C
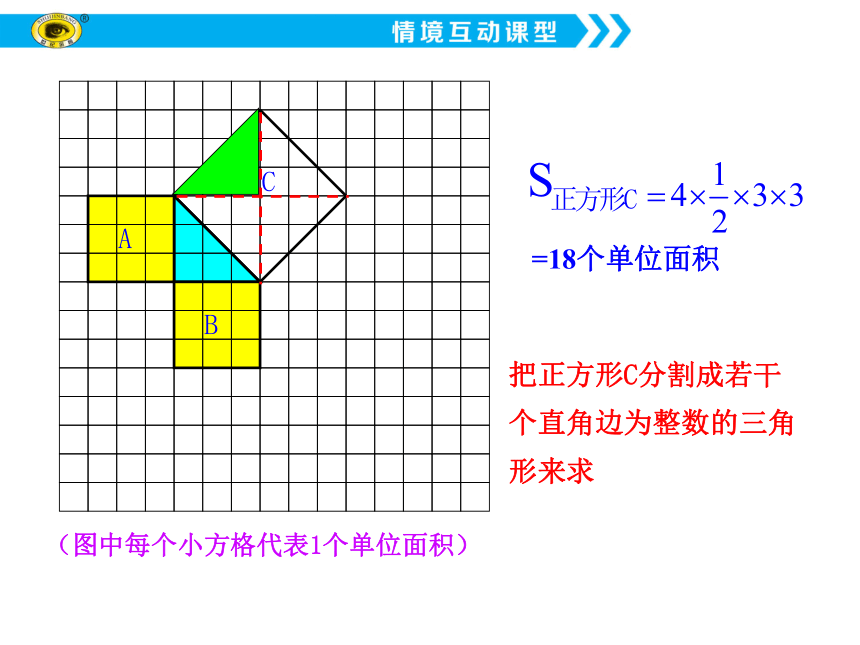
(图中每个小方格代表1个单位面积)
把正方形C分割成若干个直角边为整数的三角形来求
=18个单位面积
A
B
C
(图中每个小方格代表1个单位面积)
=18个单位面积
把正方形C看成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表1个单位面积)
图1
图2
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?图2呢?
SA+SB=SC
【结论】两条直角边上的正方形面积之和等于斜边上的正方形的面积.
结合以上问题,说一说你的结论!
A
B
C
图1
A
B
C
图2
右图中两个直角三角形三边平方之间都有什么关系?
【结论】两条直角边的平方和等于斜边的平方.
【议一议】
中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.
据《周髀算经》记载,西周战国时期(约公元前1千多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一个直角三角形,如果勾是3,股是4,那么弦等于5.
3
4
5
∟
勾
股
弦
【古人智慧】
人们还发现,
在直角三角形中,
勾是6,
股是8,
勾是5,
股是12,
弦一定是13,
所有的直角三角形都有这个性质.世界上许多数学家,先后用不同方法证明了这个结论. 我国把它称为勾股定理.
62=36,
82=64,
62+82=102
102=100
等等.
52=25,
122=144,
52+122=132
132=169
弦一定是10;
勾股定理
数学语言:如果用a,b和c分别表示直角三角形的两直角边和斜边,
文字叙述:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
【概括新知】
那么a2+b2=c2
勾2+股2=弦2
a
b
c
a
b
c
b
a
c
a
b
c
用两种方法表示大正方形的面积:
a
b
c
b
c
b
c
b
c
a
a
a
对比两种表示方法,你得到勾股定理了吗
我们用另外一种方法来说明勾股定理是正确的.
【例】如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
【例题】
【解析】设旗杆顶部到折断处的距离为x m,根据勾股定理得
92+122=x2
x=±15(负值舍去),
15+9=24(m).
答:旗杆原来高24 m.
A
B
C
如图,太阳能热水器的支架AB长为
90 cm,与AB垂直的BC长为120 cm.
太阳能真空管AC有多长
【解析】在Rt△ABC中,由勾股定理,得
AC= = =150(cm).
答:太阳能真空管AC长150 cm.
【跟踪训练】
通过本课时的学习,需要我们掌握:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,即
2.(义乌·中考)在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可)
答案:5或
5.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方3 km处,过了20 s,飞机距离这个男孩头顶5 km.这一过程中飞机飞过的距离是多少千米?
【解析】在Rt△ABC中,
答:飞机飞过的距离是4 km.
B
C
A
3
5
?
6.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
【解析】设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
所以 x=±8(负值舍去),
所以另一直角边长为8 cm,
直角三角形的面积是:
(cm2).
没有智慧的头脑,就像没有蜡烛的灯笼.
1 探索勾股定理
第一章 勾股定理
观察:图中两个正方形是怎样形成的,你知道它有什么意义吗?
这是1955年希腊为纪念一个数学学派发行的邮票.
观察:发现下面邮票中三个正方形的面积关系
1.经历探索勾股定理及验证勾股定理的过程,了解勾股定理的探究方法及其内在联系.
2.掌握勾股定理,并能运用勾股定理解决一些实际问题.
P
R
Q
正方形P的面积 正方形Q的面积 正方形R的面积
A
B
C
9
16
?
怎么求SR的大小?
有几种方案?
如图,小方格的边长为1.
【探究新知】
△ABC是什么特殊的三角形?
P
Q
C
R
用“补”的方法
SR
P
Q
C
R
用“割”的方法
Q
SR
A
B
C
(图中每个小方格代表1个单位面积)
(1)在图中,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是____个
单位面积.
正方形C的面积是_____
个单位面积.
9
9
9
18
【试一试】
A
B
C
(图中每个小方格代表1个单位面积)
把正方形C分割成若干个直角边为整数的三角形来求
=18个单位面积
A
B
C
(图中每个小方格代表1个单位面积)
=18个单位面积
把正方形C看成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表1个单位面积)
图1
图2
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?图2呢?
SA+SB=SC
【结论】两条直角边上的正方形面积之和等于斜边上的正方形的面积.
结合以上问题,说一说你的结论!
A
B
C
图1
A
B
C
图2
右图中两个直角三角形三边平方之间都有什么关系?
【结论】两条直角边的平方和等于斜边的平方.
【议一议】
中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.
据《周髀算经》记载,西周战国时期(约公元前1千多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一个直角三角形,如果勾是3,股是4,那么弦等于5.
3
4
5
∟
勾
股
弦
【古人智慧】
人们还发现,
在直角三角形中,
勾是6,
股是8,
勾是5,
股是12,
弦一定是13,
所有的直角三角形都有这个性质.世界上许多数学家,先后用不同方法证明了这个结论. 我国把它称为勾股定理.
62=36,
82=64,
62+82=102
102=100
等等.
52=25,
122=144,
52+122=132
132=169
弦一定是10;
勾股定理
数学语言:如果用a,b和c分别表示直角三角形的两直角边和斜边,
文字叙述:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
【概括新知】
那么a2+b2=c2
勾2+股2=弦2
a
b
c
a
b
c
b
a
c
a
b
c
用两种方法表示大正方形的面积:
a
b
c
b
c
b
c
b
c
a
a
a
对比两种表示方法,你得到勾股定理了吗
我们用另外一种方法来说明勾股定理是正确的.
【例】如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
【例题】
【解析】设旗杆顶部到折断处的距离为x m,根据勾股定理得
92+122=x2
x=±15(负值舍去),
15+9=24(m).
答:旗杆原来高24 m.
A
B
C
如图,太阳能热水器的支架AB长为
90 cm,与AB垂直的BC长为120 cm.
太阳能真空管AC有多长
【解析】在Rt△ABC中,由勾股定理,得
AC= = =150(cm).
答:太阳能真空管AC长150 cm.
【跟踪训练】
通过本课时的学习,需要我们掌握:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,即
2.(义乌·中考)在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可)
答案:5或
5.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方3 km处,过了20 s,飞机距离这个男孩头顶5 km.这一过程中飞机飞过的距离是多少千米?
【解析】在Rt△ABC中,
答:飞机飞过的距离是4 km.
B
C
A
3
5
?
6.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
【解析】设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
所以 x=±8(负值舍去),
所以另一直角边长为8 cm,
直角三角形的面积是:
(cm2).
没有智慧的头脑,就像没有蜡烛的灯笼.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
