2.2 课时2 二次函数y=x2+k的图像与性质 课件(共15张PPT)
文档属性
| 名称 | 2.2 课时2 二次函数y=x2+k的图像与性质 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 22:17:41 | ||
图片预览




文档简介
(共15张PPT)
第二章 二次函数
2 二次函数的图像和性质
课时2 二次函数y=x2+k的图像与性质
1.能够画出二次函数y=ax2+k的图象.
2.通过观察图象,掌握y=ax2+k的图象特征和性质. (重点)
学习目标
新课导入
1. 二次函数 y = ax2 的图象与性质
x
y
O
x
y
O
图象 位置与开口 对称性 顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于轴对称,对称轴是直线
顶点是原点(0,0)
当时,
当时,
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
2.一次函数与的图象的位置关系是怎样的?
平行
新课讲解
知识点1 二次函数y=ax2+k的图象
做一做
1.画二次函数y= x2+1的图象,你是怎样画的?与同伴进行
交流.
2.二次函数y=x2+1的图象与二次函数y=x2 的图象有什么关
系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐
标分别是什么?
二次函数y = x2-1的图象呢?
新课讲解
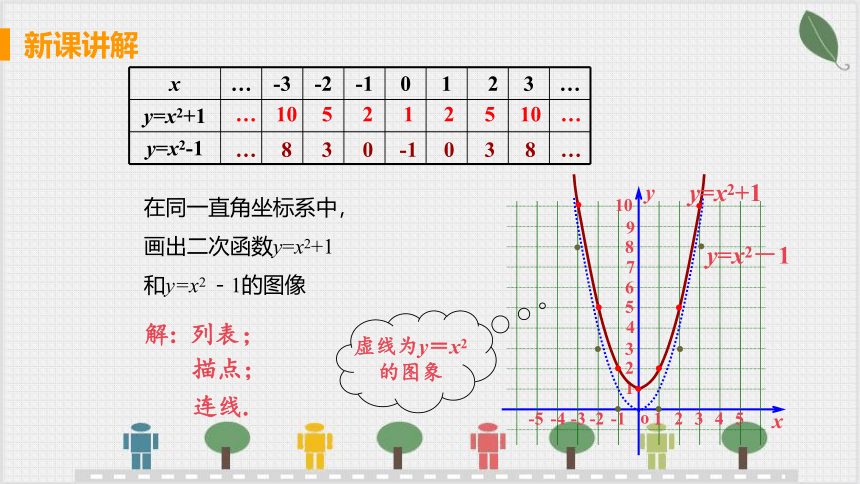
在同一直角坐标系中,画出二次函数y=x2+1和y=x2 -1的图像
解: 列表;
x … -3 -2 -1 0 1 2 3 …
y=x2+1
y=x2-1
… 10 5 2 1 2 5 10 …
… 8 3 0 -1 0 3 8 …
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=x2+1
描点;
连线.
y=x2-1
虚线为y=x2
的图象
新课讲解
例
典例分析
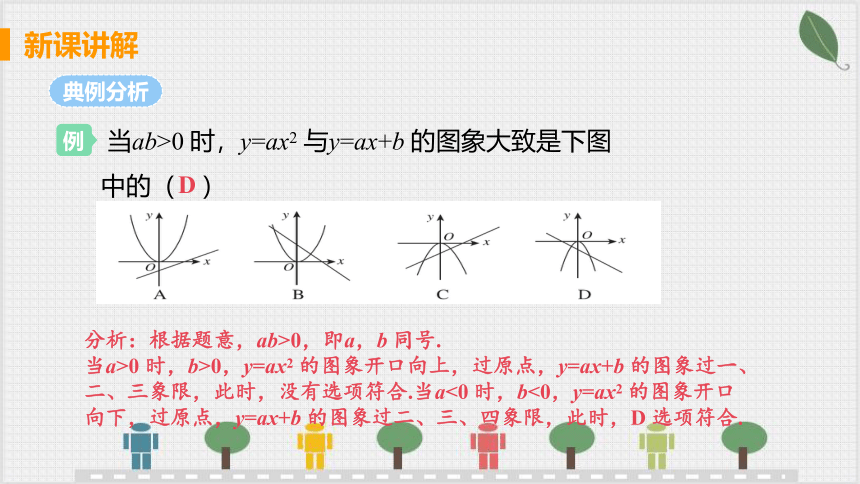
分析:根据题意,ab>0,即a,b 同号.
当a>0 时,b>0,y=ax2 的图象开口向上,过原点,y=ax+b 的图象过一、二、三象限,此时,没有选项符合.当a<0 时,b<0,y=ax2 的图象开口向下,过原点,y=ax+b 的图象过二、三、四象限,此时,D 选项符合.
当ab>0 时,y=ax2 与y=ax+b 的图象大致是下图 中的( )
D
新课讲解
练一练
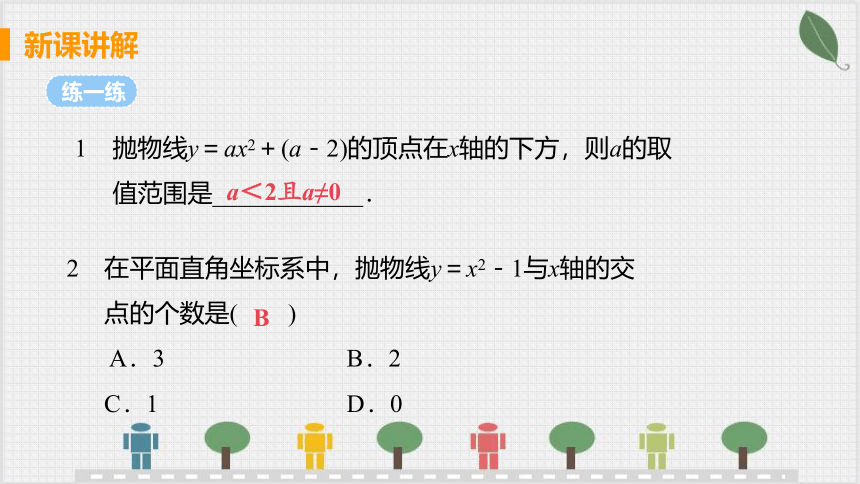
1 抛物线y=ax2+(a-2)的顶点在x轴的下方,则a的取
值范围是____________.
a<2且a≠0
2 在平面直角坐标系中,抛物线y=x2-1与x轴的交
点的个数是( )
A.3 B.2
C.1 D.0
B
新课讲解
知识点2 二次函数y=ax2+k的性质
二次函数y=ax2+k(a≠0)的图象和性质
函数 y=ax2+k(a>0) y=ax2+k(a<0)
图象 k>0
k<0
开口方向 向上 向下
顶点坐标 (0,k) (0,k)
新课讲解
函数 y=ax2+k(a>0) y=ax2+k(a<0)
对称轴 y轴(或直线x=0) y轴(或直线x=0)
增减性 当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大 当x<0时,y随x的增大而增大;当x>0时,y随
x的增大而减小
最值 当x=0时,y最小值=k 当x=0时,y最大值=k
续表:
新课讲解
练一练
对于二次函数y=3x2+2,下列说法错误的是( )
A.最小值为2
B.图象与x轴没有公共点
C.当x<0时,y随x的增大而增大
D.图象的对称轴是y轴
C
课堂小结
y=ax2+k (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增 减 性
向上
向下
(0 ,k)
(0 ,k)
y轴
y轴
当x<0时,y随着x的增大而减小.
当x>0时,y随着x的增大而增大.
当x<0时,y随着x的增大而增大.
当x>0时,y随着x的增大而减小.
二次函数y=ax2+k的图象与性质
课堂小结
二次函数y=ax2+k的图象与性质
y=ax2+k (a≠0) a>0 a<0
极值
续表
x=0时,y最小= k
x=0时,y最大=k
抛物线y=ax2 +k (a≠0)的图象可由y=ax2的图象通过上下平移|k|个单位得到.
当堂小练
填表:
函数 开口方向 顶点坐标 对称轴 有最高(低)点
向下
向上
向下
y轴
y轴
y轴
有最高点
有最低点
有最高点
拓展与延伸
能否通过上下平移二次函数y= x2的图象,使得到的新的函数图象过点(3,-3)?若能,说出平移的方向和距离;若不能,说明理由.
拓展与延伸
能.设平移后的图象对应的二次函数表达式为
y= x2+b, 将点(3,-3)的坐标代入表达式,
得b=-6.
所以平移的方向是向下,平移的距离是6个单位长度.
解:
第二章 二次函数
2 二次函数的图像和性质
课时2 二次函数y=x2+k的图像与性质
1.能够画出二次函数y=ax2+k的图象.
2.通过观察图象,掌握y=ax2+k的图象特征和性质. (重点)
学习目标
新课导入
1. 二次函数 y = ax2 的图象与性质
x
y
O
x
y
O
图象 位置与开口 对称性 顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于轴对称,对称轴是直线
顶点是原点(0,0)
当时,
当时,
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
2.一次函数与的图象的位置关系是怎样的?
平行
新课讲解
知识点1 二次函数y=ax2+k的图象
做一做
1.画二次函数y= x2+1的图象,你是怎样画的?与同伴进行
交流.
2.二次函数y=x2+1的图象与二次函数y=x2 的图象有什么关
系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐
标分别是什么?
二次函数y = x2-1的图象呢?
新课讲解
在同一直角坐标系中,画出二次函数y=x2+1和y=x2 -1的图像
解: 列表;
x … -3 -2 -1 0 1 2 3 …
y=x2+1
y=x2-1
… 10 5 2 1 2 5 10 …
… 8 3 0 -1 0 3 8 …
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=x2+1
描点;
连线.
y=x2-1
虚线为y=x2
的图象
新课讲解
例
典例分析
分析:根据题意,ab>0,即a,b 同号.
当a>0 时,b>0,y=ax2 的图象开口向上,过原点,y=ax+b 的图象过一、二、三象限,此时,没有选项符合.当a<0 时,b<0,y=ax2 的图象开口向下,过原点,y=ax+b 的图象过二、三、四象限,此时,D 选项符合.
当ab>0 时,y=ax2 与y=ax+b 的图象大致是下图 中的( )
D
新课讲解
练一练
1 抛物线y=ax2+(a-2)的顶点在x轴的下方,则a的取
值范围是____________.
a<2且a≠0
2 在平面直角坐标系中,抛物线y=x2-1与x轴的交
点的个数是( )
A.3 B.2
C.1 D.0
B
新课讲解
知识点2 二次函数y=ax2+k的性质
二次函数y=ax2+k(a≠0)的图象和性质
函数 y=ax2+k(a>0) y=ax2+k(a<0)
图象 k>0
k<0
开口方向 向上 向下
顶点坐标 (0,k) (0,k)
新课讲解
函数 y=ax2+k(a>0) y=ax2+k(a<0)
对称轴 y轴(或直线x=0) y轴(或直线x=0)
增减性 当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大 当x<0时,y随x的增大而增大;当x>0时,y随
x的增大而减小
最值 当x=0时,y最小值=k 当x=0时,y最大值=k
续表:
新课讲解
练一练
对于二次函数y=3x2+2,下列说法错误的是( )
A.最小值为2
B.图象与x轴没有公共点
C.当x<0时,y随x的增大而增大
D.图象的对称轴是y轴
C
课堂小结
y=ax2+k (a≠0) a>0 a<0
开口方向
顶点坐标
对称轴
增 减 性
向上
向下
(0 ,k)
(0 ,k)
y轴
y轴
当x<0时,y随着x的增大而减小.
当x>0时,y随着x的增大而增大.
当x<0时,y随着x的增大而增大.
当x>0时,y随着x的增大而减小.
二次函数y=ax2+k的图象与性质
课堂小结
二次函数y=ax2+k的图象与性质
y=ax2+k (a≠0) a>0 a<0
极值
续表
x=0时,y最小= k
x=0时,y最大=k
抛物线y=ax2 +k (a≠0)的图象可由y=ax2的图象通过上下平移|k|个单位得到.
当堂小练
填表:
函数 开口方向 顶点坐标 对称轴 有最高(低)点
向下
向上
向下
y轴
y轴
y轴
有最高点
有最低点
有最高点
拓展与延伸
能否通过上下平移二次函数y= x2的图象,使得到的新的函数图象过点(3,-3)?若能,说出平移的方向和距离;若不能,说明理由.
拓展与延伸
能.设平移后的图象对应的二次函数表达式为
y= x2+b, 将点(3,-3)的坐标代入表达式,
得b=-6.
所以平移的方向是向下,平移的距离是6个单位长度.
解:
