2021-2022学年鲁教版(五四制)数学七年级上册5.2 平面直角坐标系 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)数学七年级上册5.2 平面直角坐标系 同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 142.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 00:00:00 | ||
图片预览



文档简介
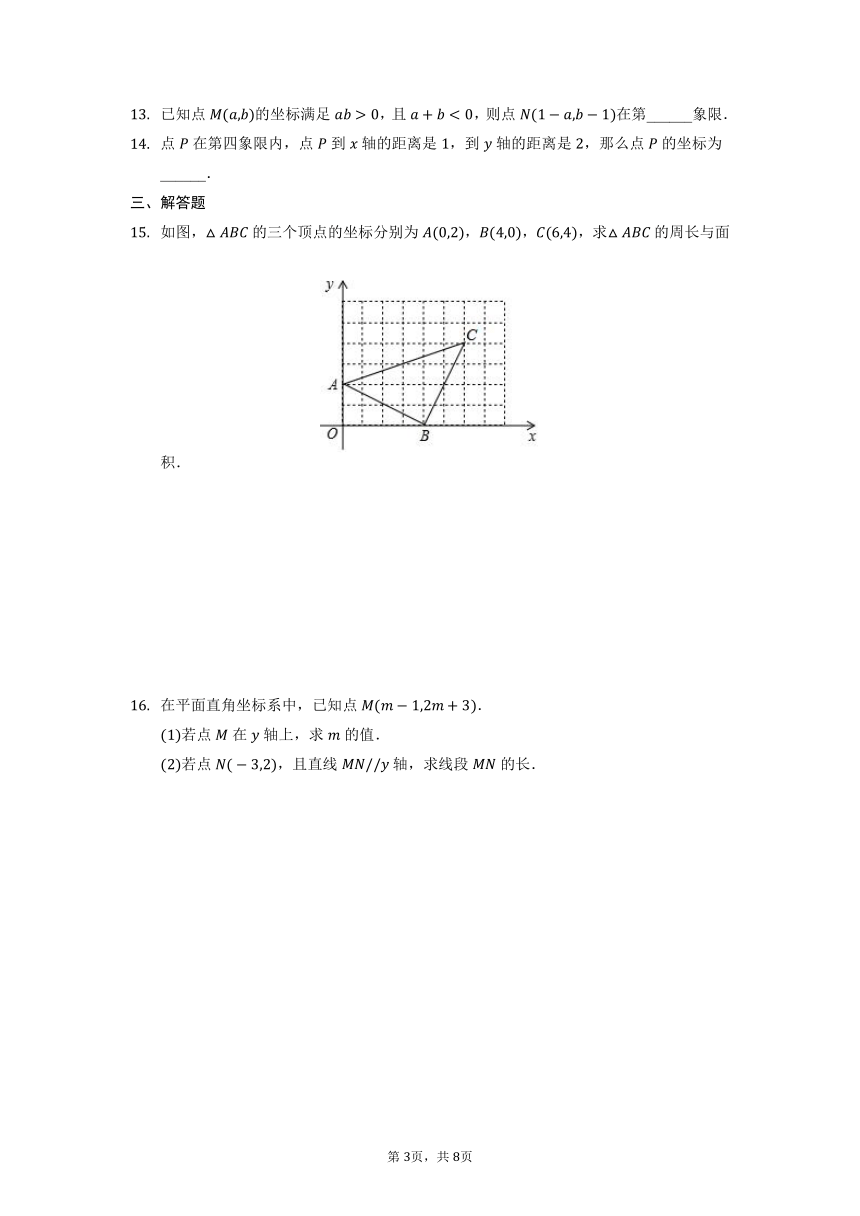
平面直角坐标系
一、选择题
在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,则点的坐标为
A. B. C. D.
如果在第四象限,那么在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
已知点在轴上,则点的坐标是
A. B. C. D.
如图,四边形是正方形,,两点的坐标分别是,,点在第一象限,则点的坐标是
A. B. C. D.
在平面直角坐标系中,若点在第四象限内,则点所在的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
小莹和小博士下棋,小莹执圆子,小博士执方子。如图,棋盘中心方子的位置用表示,右下角方子的位置用表示小莹将第枚圆子放入棋盘后,所有棋子构成一个轴对称图形。她放的位置是
A. B. C. D.
如图,下列各点中在阴影区域内的是
A.
B.
C.
D.
已知点到两坐标轴的距离相等,则的值为
A. B. C. 或 D.
如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿将其放在平面直角坐标系中,表示叶片“顶部”,两点的坐标分别为,,则叶杆“底部”点的坐标为
A.
B.
C.
D.
在平面直角坐标系中,长为的线段点在点右侧在轴上移动,,,连接,,则的最小值为
A. B. C. D.
二、填空题
如图,在一单位为的方格纸上,,,,,都是斜边在轴上、斜边长分别为,,,的等腰直角三角形.若的顶点坐标分别为,,,则依图中所示规律,的坐标为______.
已知点和点,若直线轴,且,则的值______.
已知点的坐标满足,且,则点在第______象限.
点在第四象限内,点到轴的距离是,到轴的距离是,那么点的坐标为______.
三、解答题
如图,的三个顶点的坐标分别为,,,求的周长与面积.
在平面直角坐标系中,已知点.
若点在轴上,求的值.
若点,且直线轴,求线段的长.
答案和解析
1.【答案】
【解答】
解:在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,
点的纵坐标为:,横坐标为:,
即点的坐标为:.
故选:.
2.【答案】
【解析】解:在第四象限,
,,
,,
,
在第二象限.
3.【答案】
【解析】解:点在轴上,
,
解得:,
故,
故点的坐标为:.
4.【答案】
【解析】解:四边形是正方形,
,,
,两点的坐标分别是,,
,
,
.
5.【答案】
【解析】解:点在第四象限内,
,
则点所在的象限是第二象限,
6.【答案】
【解答】
解:棋盘中心方子的位置用表示,则这点所在的横线是轴,右下角方子的位置用,则这点所在的纵线是轴,则当放的位置是时构成轴对称图形.
故选B
7.【答案】
【解答】
解:在第一象限,在所示区域;
B.在第二象限,不在所示区域;
C.在第四象限,不在所示区域;
D.在第三象限,不在所示区域.
故选A.
8.【答案】
【解答】
解:由题意,得
或,
解得或,
故选C.
9.【答案】
【解答】
解:,两点的坐标分别为,,
得出坐标轴如下图所示位置:
点的坐标为.
故答案为:.
10.【答案】
【解析】解:设,
,
,
,,
,
要求的最小值,相当于在轴上找一点,使得点到和的距离和最小,,
如图中,作点关于原点的对称点,连接交轴于,连接,此时的值最小,
,
的最小值,
的最小值为.
故选:.
设,则有,推出要求的最小值,相当于在轴上找一点,使得点到和的距离和最小,如图中,作点关于原点的对称点,连接交轴于,连接,此时的值最小,求出即可解决问题.
11.【答案】
【解析】解:各三角形都是等腰直角三角形,
直角顶点的纵坐标的长度为斜边的一半,
,,,,,,,,,,,,,
由上可知,当脚码是、、时,横坐标是脚码加和的一半,纵坐标为;当脚码是、、时,横坐标为,纵坐标为脚码的一半的相反数;当脚码是、、时,横坐标是脚码减差的一半的相反数,纵坐标为;当脚码是、、时,横坐标是,纵坐标为脚码的一半.
,
点在轴负半轴上,横坐标是,纵坐标是,
的坐标为.
12.【答案】或
【解析】解:点和点且直线轴,
,
,
或,
当时,;
当时,;
综上,或;
13.【答案】四
【解析】解:,
、同号,
,
,,
,,
点在第四象限.
14.【答案】
【解答】
解:因为点在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点到轴的距离为,到轴的距离为,
所以点的横坐标为,纵坐标为.
所以点的坐标为.
故答案为:.
15.【答案】解:,,,
,,,
的周长;
,
为直角三角形,,
的面积.
16.【答案】解:由题意得:,
解得:;
点,且直线轴,
,
解得.
,
.
第2页,共2页
第1页,共3页
一、选择题
在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,则点的坐标为
A. B. C. D.
如果在第四象限,那么在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
已知点在轴上,则点的坐标是
A. B. C. D.
如图,四边形是正方形,,两点的坐标分别是,,点在第一象限,则点的坐标是
A. B. C. D.
在平面直角坐标系中,若点在第四象限内,则点所在的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
小莹和小博士下棋,小莹执圆子,小博士执方子。如图,棋盘中心方子的位置用表示,右下角方子的位置用表示小莹将第枚圆子放入棋盘后,所有棋子构成一个轴对称图形。她放的位置是
A. B. C. D.
如图,下列各点中在阴影区域内的是
A.
B.
C.
D.
已知点到两坐标轴的距离相等,则的值为
A. B. C. 或 D.
如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿将其放在平面直角坐标系中,表示叶片“顶部”,两点的坐标分别为,,则叶杆“底部”点的坐标为
A.
B.
C.
D.
在平面直角坐标系中,长为的线段点在点右侧在轴上移动,,,连接,,则的最小值为
A. B. C. D.
二、填空题
如图,在一单位为的方格纸上,,,,,都是斜边在轴上、斜边长分别为,,,的等腰直角三角形.若的顶点坐标分别为,,,则依图中所示规律,的坐标为______.
已知点和点,若直线轴,且,则的值______.
已知点的坐标满足,且,则点在第______象限.
点在第四象限内,点到轴的距离是,到轴的距离是,那么点的坐标为______.
三、解答题
如图,的三个顶点的坐标分别为,,,求的周长与面积.
在平面直角坐标系中,已知点.
若点在轴上,求的值.
若点,且直线轴,求线段的长.
答案和解析
1.【答案】
【解答】
解:在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,
点的纵坐标为:,横坐标为:,
即点的坐标为:.
故选:.
2.【答案】
【解析】解:在第四象限,
,,
,,
,
在第二象限.
3.【答案】
【解析】解:点在轴上,
,
解得:,
故,
故点的坐标为:.
4.【答案】
【解析】解:四边形是正方形,
,,
,两点的坐标分别是,,
,
,
.
5.【答案】
【解析】解:点在第四象限内,
,
则点所在的象限是第二象限,
6.【答案】
【解答】
解:棋盘中心方子的位置用表示,则这点所在的横线是轴,右下角方子的位置用,则这点所在的纵线是轴,则当放的位置是时构成轴对称图形.
故选B
7.【答案】
【解答】
解:在第一象限,在所示区域;
B.在第二象限,不在所示区域;
C.在第四象限,不在所示区域;
D.在第三象限,不在所示区域.
故选A.
8.【答案】
【解答】
解:由题意,得
或,
解得或,
故选C.
9.【答案】
【解答】
解:,两点的坐标分别为,,
得出坐标轴如下图所示位置:
点的坐标为.
故答案为:.
10.【答案】
【解析】解:设,
,
,
,,
,
要求的最小值,相当于在轴上找一点,使得点到和的距离和最小,,
如图中,作点关于原点的对称点,连接交轴于,连接,此时的值最小,
,
的最小值,
的最小值为.
故选:.
设,则有,推出要求的最小值,相当于在轴上找一点,使得点到和的距离和最小,如图中,作点关于原点的对称点,连接交轴于,连接,此时的值最小,求出即可解决问题.
11.【答案】
【解析】解:各三角形都是等腰直角三角形,
直角顶点的纵坐标的长度为斜边的一半,
,,,,,,,,,,,,,
由上可知,当脚码是、、时,横坐标是脚码加和的一半,纵坐标为;当脚码是、、时,横坐标为,纵坐标为脚码的一半的相反数;当脚码是、、时,横坐标是脚码减差的一半的相反数,纵坐标为;当脚码是、、时,横坐标是,纵坐标为脚码的一半.
,
点在轴负半轴上,横坐标是,纵坐标是,
的坐标为.
12.【答案】或
【解析】解:点和点且直线轴,
,
,
或,
当时,;
当时,;
综上,或;
13.【答案】四
【解析】解:,
、同号,
,
,,
,,
点在第四象限.
14.【答案】
【解答】
解:因为点在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点到轴的距离为,到轴的距离为,
所以点的横坐标为,纵坐标为.
所以点的坐标为.
故答案为:.
15.【答案】解:,,,
,,,
的周长;
,
为直角三角形,,
的面积.
16.【答案】解:由题意得:,
解得:;
点,且直线轴,
,
解得.
,
.
第2页,共2页
第1页,共3页
