12.2 三角形全等的判定 课后培优 练习2021-2022学年人教版(2012)八年级数学上册(word版 含答案)
文档属性
| 名称 | 12.2 三角形全等的判定 课后培优 练习2021-2022学年人教版(2012)八年级数学上册(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 543.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 22:23:48 | ||
图片预览



文档简介
12.2 三角形全等的判定
一、单选题
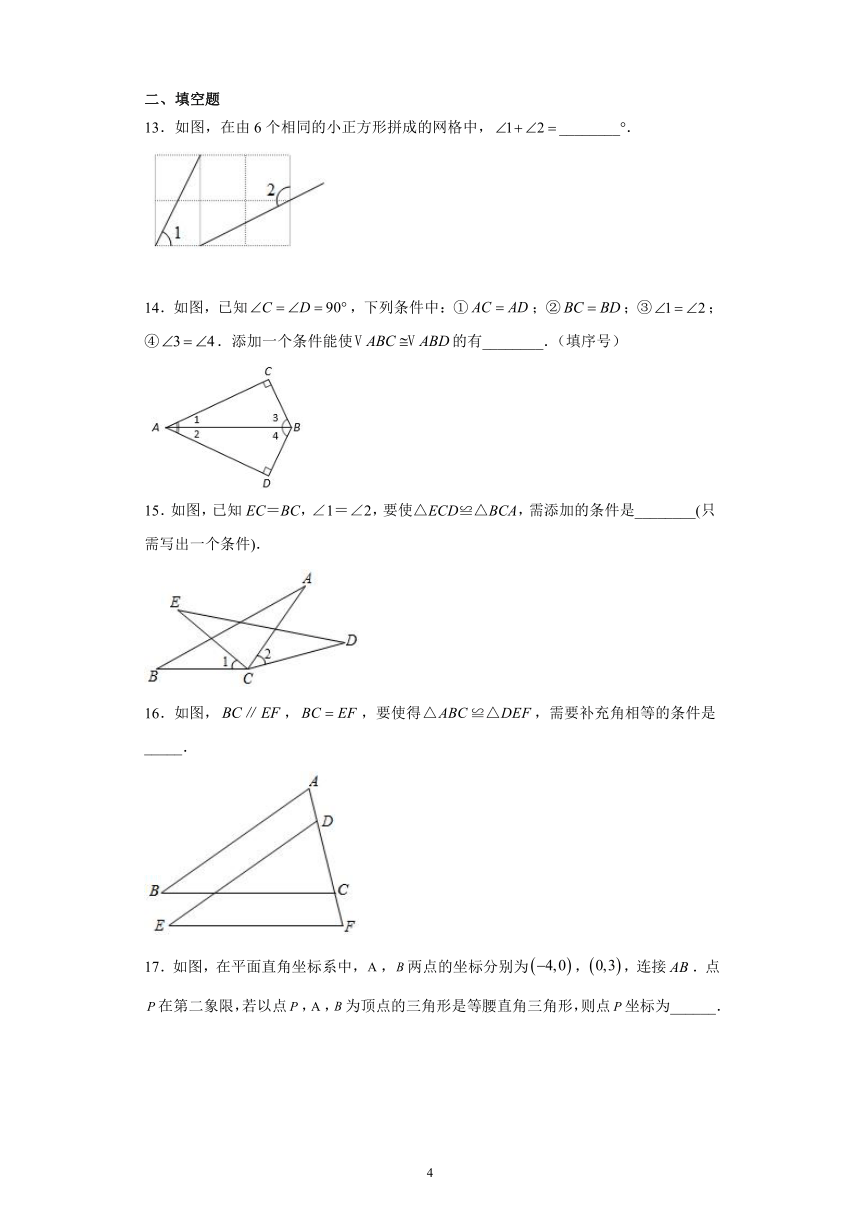
1.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长( )
A.3 B.5 C.6 D.7
2.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD 面积相等;③BF∥CE;④CE=BF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知,,则直接判定的根据是( )
A. B. C. D.
4.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列条件无法直接证明△ABC≌△DEF的是( )
A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F
5.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=( )
A.3 B.4 C.5 D.6
6.如图所示,H是的高AD,BE的交点,且,则下列结论:①;②;③;④.正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,一块玻璃碎成三片,小智只带了第③块去玻璃店,就能配一块一模一样的玻璃,你能用三角形的知识解释,这是为什么?( )
A. B. C. D.
8.小茜同学用三角形全等的知识测量A、B两点间的距离时,先在平面上选取一点C,可以直接到达点A、点B,且使BC⊥AB.再延长BC至点D,使CD=BC,过点D作DE⊥BC与AC的延长线交于点E,于是她测出DE的长为16 cm,便认为A、B两点间的距离为16 cm,小茜同学这样做的数学道理是( )
A.SSS B.SAS C.ASA D.以上都不对
9.如图,AB⊥BD,DE⊥BD,垂足分别为B,D,如果∠A=25°,BC=CD,那么下列结论中,错误的是( )
A.∠ACB=25° B.∠ABC=90° C.AC=CE D.∠DCE=65°
10.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于点H且HD=DC,那么下列结论中,正确的是( )
A.△AHE≌△BHD B.HE=EC
C.AH=BD D.△ABD是等腰直角三角形
11.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点,测得∠ABC=75°,∠ACB=65°,然后在M处立了标杆,使∠CBM=75°,∠MCB=65°,得到MBC≌ABC,所以测得MB的长就是A,B两点间的距离,这里判定MBC≌ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
12.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E B.AC=DF C.∠ACD=∠BFE D.BC=EF
二、填空题
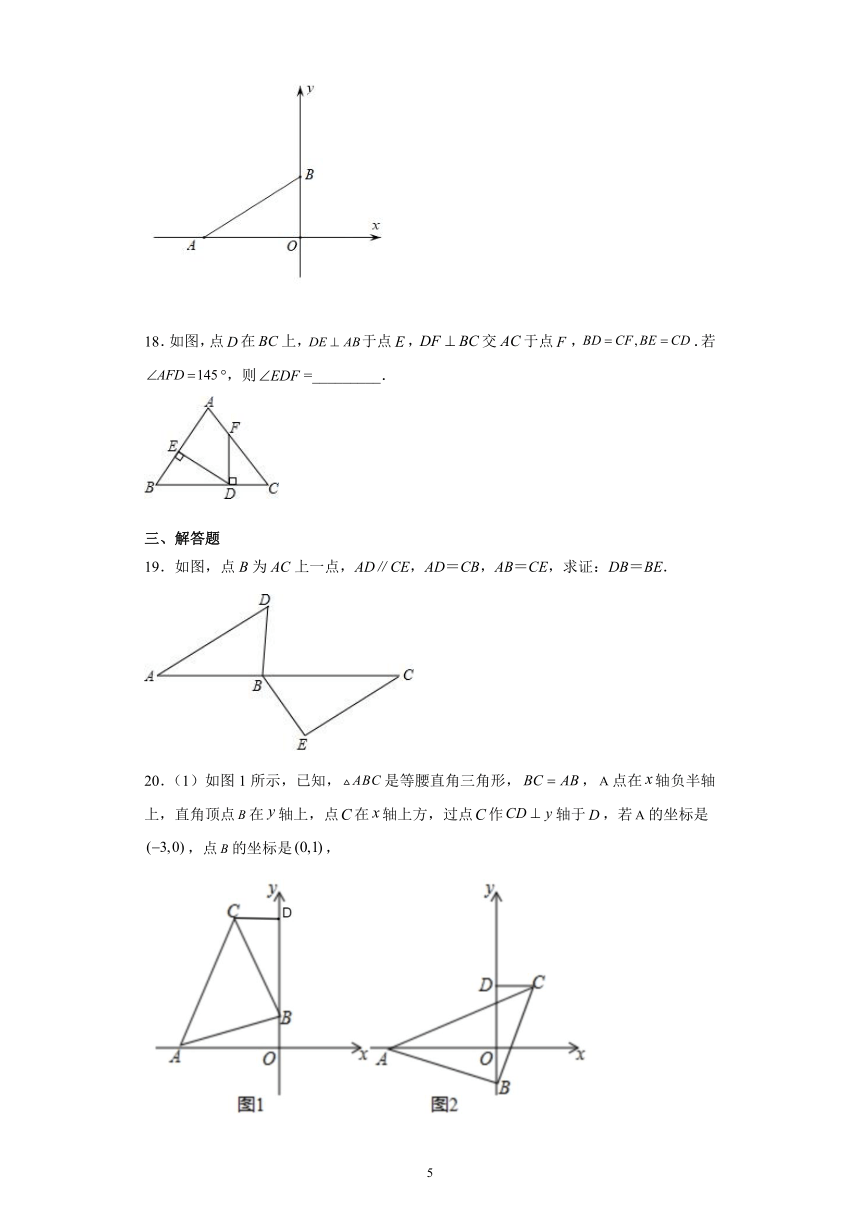
13.如图,在由6个相同的小正方形拼成的网格中,________°.
14.如图,已知,下列条件中:①;②;③;④.添加一个条件能使的有________.(填序号)
15.如图,已知EC=BC,∠1=∠2,要使△ECD≌△BCA,需添加的条件是________(只需写出一个条件).
16.如图,,,要使得,需要补充角相等的条件是_____.
17.如图,在平面直角坐标系中,,两点的坐标分别为,,连接.点在第二象限,若以点,,为顶点的三角形是等腰直角三角形,则点坐标为______.
18.如图,点在上,于点,交于点,.若°,则=_________.
三、解答题
19.如图,点B为AC上一点,AD∥CE,AD=CB,AB=CE,求证:DB=BE.
20.(1)如图1所示,已知,是等腰直角三角形,,点在轴负半轴上,直角顶点在轴上,点在轴上方,过点作轴于,若的坐标是,点的坐标是,
(1)点的坐标是 ;
(2)由图1可得,线段、、之间存在的数量关系 ;
(3)如图2,当旋转到图2位置时,是等腰直角三角形,,(2)中的结论是否还成立,并说明理由.
21.如图,在中,,于点D,点E为上的一点,且,延长交于点F,连接.
(1)求证:;
(2)若,,求的值.(用含a,b的式子表示)
22.如图,,,,求证:.
23.如图,、、、在同一条直线上,AB∥EF,BD=CE,AB=EF,求证: AC=DF.
参考答案
1.B
证明:∵CE⊥AD,BF⊥AD,
∴∠CED=∠AFB=90°,
∴∠C+∠D=90°,
∵AB⊥CD,
∴∠A+∠D=90°,
∴∠A=∠C,
在ABF与CDE中
∴ABF≌CDE(AAS),
∴BF=DE=3,CE=AF=4,
∵EF=2,
∴AE=AF-EF=4-2=2,
∴AE=2,
∴AD=AE+DE=5,
故选:B.
2.D
解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE,①正确;
∵AD是△ABC的中线,
∴△ABD和△ACD面积相等,②正确;
∵△BDF≌△CDE,
∴∠F=∠CDF,
∴BF∥CE,③正确;
∵△BDF≌△CDE,
∴CE=BF,④正确,
故选:D.
3.A
解:∵,,AB=AB,
∴(),
故选A.
4.C
解:A、若添加AC∥DF可得∠ACB=∠F,进而结合已知条件可根据“AAS”判定△ABC≌△DEF,故不符合题意;
B、若添加∠A=∠D,则结合已知条件可根据“ASA”判定△ABC≌△DEF,故不符合题意;
C、若添加AC=DF,则无法判定△ABC≌△DEF,故符合题意;
D、若添加∠ACB=∠F,可根据已知条件结合“AAS”判定△ABC≌△DEF,故不符合题意;
故选C.
5.A
解:在和中
∴
∴
∴
故选A
6.C
解:①∵BE⊥AC,AD⊥BC
∴∠AEH=∠ADB=90°
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE
∴∠HBD=∠EAH
∵DH=DC
∴△BDH≌△ADC(AAS)
∴BD=AD,①正确;
②:∵由①知,△BDH≌△ADC(AAS)
∴AC=BH,
∵在△BCE中,
∴,
∴结论②正确;
③:由①证明知,△BDH≌△ADC,
∴BH=AC,③正确;
④:由①知,△BDH≌△ADC,
∴CD=DH,
∵在△BCE中,
∴,
∴结论④错误;
综上所述,结论①②,③为正确结论.
故选:C.
7.A
解:第③块不仅保留了原来三角形的两个角还保留了一边,
则可以根据ASA来配一块一样的玻璃.应带③去.
故选A.
8.C
解:根据题意,画出图形,如图所示,
由题意,得BC=DC,∠B=∠CDE=90°,
在△ABC和△EDC中,
∵
∴△ABC≌△EDC( ASA).
∴
故答案为:C.
9.A
解:∵AB⊥BD,DE⊥BD,
∴,
故选项正确;
∵BC=CD,,
∴,
∴AC=,
故C选项正确,
∵∠A=25°,
∴,
故选项错误,选项正确;
故选:A.
10.D
解:∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∴∠DAE+∠AHE=90°,
∵BE⊥AC,
∴∠HBD+∠BHD=90°,
∵∠AHE=∠BHD,
∴∠HAE=∠HBD,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠BDA=90°,
∴△ABD是等腰直角三角形,
故选:D.
11.D
解:在△ABC和△MBC中,
,
∴△MBC≌△ABC(ASA),
故选:D.
12.D
解:∵∠A=∠D,AB=DE,
∴当添加∠B=∠E时,根据 ASA 判定△ABC≌△DEF;
当添加AC=DF时,根据 SAS 判定△ABC≌△DEF;
当添加∠ACD=∠BFE时,则∠ACB=∠DFE,根据 AAS 判定△ABC≌△DEF.
故选:D.
13.180
解:∵AC=CD,BC=DE,∠ACB=∠D=90°,
∴,
∴∠1=∠CED,
∴∠CED+∠2=180°.
故答案是:180
14.①②③④
解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);;
③当时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,可得△ABC≌△ABD(AAS);
④当时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得△ABC≌△ABD(AAS)
故答案为:①②③④.
15.DC=AC(答案不唯一)
解:添加的条件是DC=AC,理由如下:
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ECD=∠BCA,
在△ECD和△BCA中,
,
∴△ECD≌△BCA(SAS).
故答案为DC=AC.
16.∠B=∠E或∠A=∠EDF
解:∵BC∥EF,
∴∠ACB=∠F,
又BC=EF,
∴添加∠B=∠E,依据判定定理ASA,能推出△ABC≌△DEF,
添加∠A=∠EDF,依据判定定理AAS,能推出△ABC≌△DEF,
故答案为∠B=∠E或∠A=∠EDF.
17.或或
解:∵,两点的坐标分别为,
∴,
1)如图,当时,作,轴,则
可得四边形为矩形,
又∵
∴
又∵,
∴
∴,
设,则,解得
即
2)如图,当时,作轴,则
同理可证:
∴,
3)如图,当时,作轴,则
同理可证:
∴,
故答案为或或
18.55°
解:∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
∵,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∵∠EDF+∠BDE=90°,
∴∠EDF=55°.
故答案是:55°.
19.证明见详解.
证明:∵AD∥CE,
∴∠A=∠C,
在△DAB和△BCE中
∴△DAB≌△BCE(SAS),
∴DB=BE.
20.(1)(-1,4);(2);(3)不成立,理由见详解.
解:(1)∵点A的坐标是(-3,0),点B的坐标是(0,1),
∴OA=3,OB=1,
∵△ABC是等腰直角三角形,
∴BA=BC,∠ABC=90°,
∴∠ABO+∠CBD=90°,
∵∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
在△ABO和△BCD中
∵,
∴△ABO≌△BCD,
∴OB=CD=1,OA=BD=3,
∴OD=OB+BD=1+3=4,
∴C(-1,4),
故答案为:(-1,4);
(2)由(1)可知△ABO≌△BCD,
∴,
∴,
故答案为:;
(3)不成立,理由如下:
∵CD⊥y轴,
∴∠CDB=90°,∠DCB+∠CBD=90°,
∵∠ABC=90°,
∴∠ABO+∠CBD=90°,
∴∠ABO=∠DCB,
在△ABO和△BCD中
,
∴△ABO≌△BCD,
∴BO=CD,OA=DB,
∵BD=OB+OD,
∴OA=CD+OD.
21.(1)见详解;(2)
(1)证明:∵,,
∴∠BAD=180°-90°-45°=45°,∠BDE=∠ADC=90°,
∴∠ABC=∠BAD,
∴BD=AD,
又∵,
∴(HL);
(2)过点D作DM⊥BE,DN⊥AC,
∵,
∴DM=DN,
∴.
22.见详解
证明:∵∠1=∠2,
∴∠1+∠ECB=∠2+∠DCA,
即∠ACB=∠DCE,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS),
∴AB=DE.
23.见详解
证明:AB∥EF,
∴∠B=∠E
∵BD=CE
∴BD-CD=CE-CD
即BC=DE
又AB=EF
△ABC≌△FED(SAS)
AC=DF
一、单选题
1.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长( )
A.3 B.5 C.6 D.7
2.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD 面积相等;③BF∥CE;④CE=BF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知,,则直接判定的根据是( )
A. B. C. D.
4.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列条件无法直接证明△ABC≌△DEF的是( )
A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F
5.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=( )
A.3 B.4 C.5 D.6
6.如图所示,H是的高AD,BE的交点,且,则下列结论:①;②;③;④.正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,一块玻璃碎成三片,小智只带了第③块去玻璃店,就能配一块一模一样的玻璃,你能用三角形的知识解释,这是为什么?( )
A. B. C. D.
8.小茜同学用三角形全等的知识测量A、B两点间的距离时,先在平面上选取一点C,可以直接到达点A、点B,且使BC⊥AB.再延长BC至点D,使CD=BC,过点D作DE⊥BC与AC的延长线交于点E,于是她测出DE的长为16 cm,便认为A、B两点间的距离为16 cm,小茜同学这样做的数学道理是( )
A.SSS B.SAS C.ASA D.以上都不对
9.如图,AB⊥BD,DE⊥BD,垂足分别为B,D,如果∠A=25°,BC=CD,那么下列结论中,错误的是( )
A.∠ACB=25° B.∠ABC=90° C.AC=CE D.∠DCE=65°
10.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于点H且HD=DC,那么下列结论中,正确的是( )
A.△AHE≌△BHD B.HE=EC
C.AH=BD D.△ABD是等腰直角三角形
11.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点,测得∠ABC=75°,∠ACB=65°,然后在M处立了标杆,使∠CBM=75°,∠MCB=65°,得到MBC≌ABC,所以测得MB的长就是A,B两点间的距离,这里判定MBC≌ABC的理由是( )
A.SAS B.AAA C.SSS D.ASA
12.如图,在△ABC和△DEF中,点B、F、C、D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E B.AC=DF C.∠ACD=∠BFE D.BC=EF
二、填空题
13.如图,在由6个相同的小正方形拼成的网格中,________°.
14.如图,已知,下列条件中:①;②;③;④.添加一个条件能使的有________.(填序号)
15.如图,已知EC=BC,∠1=∠2,要使△ECD≌△BCA,需添加的条件是________(只需写出一个条件).
16.如图,,,要使得,需要补充角相等的条件是_____.
17.如图,在平面直角坐标系中,,两点的坐标分别为,,连接.点在第二象限,若以点,,为顶点的三角形是等腰直角三角形,则点坐标为______.
18.如图,点在上,于点,交于点,.若°,则=_________.
三、解答题
19.如图,点B为AC上一点,AD∥CE,AD=CB,AB=CE,求证:DB=BE.
20.(1)如图1所示,已知,是等腰直角三角形,,点在轴负半轴上,直角顶点在轴上,点在轴上方,过点作轴于,若的坐标是,点的坐标是,
(1)点的坐标是 ;
(2)由图1可得,线段、、之间存在的数量关系 ;
(3)如图2,当旋转到图2位置时,是等腰直角三角形,,(2)中的结论是否还成立,并说明理由.
21.如图,在中,,于点D,点E为上的一点,且,延长交于点F,连接.
(1)求证:;
(2)若,,求的值.(用含a,b的式子表示)
22.如图,,,,求证:.
23.如图,、、、在同一条直线上,AB∥EF,BD=CE,AB=EF,求证: AC=DF.
参考答案
1.B
证明:∵CE⊥AD,BF⊥AD,
∴∠CED=∠AFB=90°,
∴∠C+∠D=90°,
∵AB⊥CD,
∴∠A+∠D=90°,
∴∠A=∠C,
在ABF与CDE中
∴ABF≌CDE(AAS),
∴BF=DE=3,CE=AF=4,
∵EF=2,
∴AE=AF-EF=4-2=2,
∴AE=2,
∴AD=AE+DE=5,
故选:B.
2.D
解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE,①正确;
∵AD是△ABC的中线,
∴△ABD和△ACD面积相等,②正确;
∵△BDF≌△CDE,
∴∠F=∠CDF,
∴BF∥CE,③正确;
∵△BDF≌△CDE,
∴CE=BF,④正确,
故选:D.
3.A
解:∵,,AB=AB,
∴(),
故选A.
4.C
解:A、若添加AC∥DF可得∠ACB=∠F,进而结合已知条件可根据“AAS”判定△ABC≌△DEF,故不符合题意;
B、若添加∠A=∠D,则结合已知条件可根据“ASA”判定△ABC≌△DEF,故不符合题意;
C、若添加AC=DF,则无法判定△ABC≌△DEF,故符合题意;
D、若添加∠ACB=∠F,可根据已知条件结合“AAS”判定△ABC≌△DEF,故不符合题意;
故选C.
5.A
解:在和中
∴
∴
∴
故选A
6.C
解:①∵BE⊥AC,AD⊥BC
∴∠AEH=∠ADB=90°
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE
∴∠HBD=∠EAH
∵DH=DC
∴△BDH≌△ADC(AAS)
∴BD=AD,①正确;
②:∵由①知,△BDH≌△ADC(AAS)
∴AC=BH,
∵在△BCE中,
∴,
∴结论②正确;
③:由①证明知,△BDH≌△ADC,
∴BH=AC,③正确;
④:由①知,△BDH≌△ADC,
∴CD=DH,
∵在△BCE中,
∴,
∴结论④错误;
综上所述,结论①②,③为正确结论.
故选:C.
7.A
解:第③块不仅保留了原来三角形的两个角还保留了一边,
则可以根据ASA来配一块一样的玻璃.应带③去.
故选A.
8.C
解:根据题意,画出图形,如图所示,
由题意,得BC=DC,∠B=∠CDE=90°,
在△ABC和△EDC中,
∵
∴△ABC≌△EDC( ASA).
∴
故答案为:C.
9.A
解:∵AB⊥BD,DE⊥BD,
∴,
故选项正确;
∵BC=CD,,
∴,
∴AC=,
故C选项正确,
∵∠A=25°,
∴,
故选项错误,选项正确;
故选:A.
10.D
解:∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∴∠DAE+∠AHE=90°,
∵BE⊥AC,
∴∠HBD+∠BHD=90°,
∵∠AHE=∠BHD,
∴∠HAE=∠HBD,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠BDA=90°,
∴△ABD是等腰直角三角形,
故选:D.
11.D
解:在△ABC和△MBC中,
,
∴△MBC≌△ABC(ASA),
故选:D.
12.D
解:∵∠A=∠D,AB=DE,
∴当添加∠B=∠E时,根据 ASA 判定△ABC≌△DEF;
当添加AC=DF时,根据 SAS 判定△ABC≌△DEF;
当添加∠ACD=∠BFE时,则∠ACB=∠DFE,根据 AAS 判定△ABC≌△DEF.
故选:D.
13.180
解:∵AC=CD,BC=DE,∠ACB=∠D=90°,
∴,
∴∠1=∠CED,
∴∠CED+∠2=180°.
故答案是:180
14.①②③④
解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);;
③当时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,可得△ABC≌△ABD(AAS);
④当时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得△ABC≌△ABD(AAS)
故答案为:①②③④.
15.DC=AC(答案不唯一)
解:添加的条件是DC=AC,理由如下:
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ECD=∠BCA,
在△ECD和△BCA中,
,
∴△ECD≌△BCA(SAS).
故答案为DC=AC.
16.∠B=∠E或∠A=∠EDF
解:∵BC∥EF,
∴∠ACB=∠F,
又BC=EF,
∴添加∠B=∠E,依据判定定理ASA,能推出△ABC≌△DEF,
添加∠A=∠EDF,依据判定定理AAS,能推出△ABC≌△DEF,
故答案为∠B=∠E或∠A=∠EDF.
17.或或
解:∵,两点的坐标分别为,
∴,
1)如图,当时,作,轴,则
可得四边形为矩形,
又∵
∴
又∵,
∴
∴,
设,则,解得
即
2)如图,当时,作轴,则
同理可证:
∴,
3)如图,当时,作轴,则
同理可证:
∴,
故答案为或或
18.55°
解:∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
∵,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∵∠EDF+∠BDE=90°,
∴∠EDF=55°.
故答案是:55°.
19.证明见详解.
证明:∵AD∥CE,
∴∠A=∠C,
在△DAB和△BCE中
∴△DAB≌△BCE(SAS),
∴DB=BE.
20.(1)(-1,4);(2);(3)不成立,理由见详解.
解:(1)∵点A的坐标是(-3,0),点B的坐标是(0,1),
∴OA=3,OB=1,
∵△ABC是等腰直角三角形,
∴BA=BC,∠ABC=90°,
∴∠ABO+∠CBD=90°,
∵∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
在△ABO和△BCD中
∵,
∴△ABO≌△BCD,
∴OB=CD=1,OA=BD=3,
∴OD=OB+BD=1+3=4,
∴C(-1,4),
故答案为:(-1,4);
(2)由(1)可知△ABO≌△BCD,
∴,
∴,
故答案为:;
(3)不成立,理由如下:
∵CD⊥y轴,
∴∠CDB=90°,∠DCB+∠CBD=90°,
∵∠ABC=90°,
∴∠ABO+∠CBD=90°,
∴∠ABO=∠DCB,
在△ABO和△BCD中
,
∴△ABO≌△BCD,
∴BO=CD,OA=DB,
∵BD=OB+OD,
∴OA=CD+OD.
21.(1)见详解;(2)
(1)证明:∵,,
∴∠BAD=180°-90°-45°=45°,∠BDE=∠ADC=90°,
∴∠ABC=∠BAD,
∴BD=AD,
又∵,
∴(HL);
(2)过点D作DM⊥BE,DN⊥AC,
∵,
∴DM=DN,
∴.
22.见详解
证明:∵∠1=∠2,
∴∠1+∠ECB=∠2+∠DCA,
即∠ACB=∠DCE,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS),
∴AB=DE.
23.见详解
证明:AB∥EF,
∴∠B=∠E
∵BD=CE
∴BD-CD=CE-CD
即BC=DE
又AB=EF
△ABC≌△FED(SAS)
AC=DF
