2021-2022学年鲁教版(五四制)数学七年级上册6.5 一次函数的应用 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)数学七年级上册6.5 一次函数的应用 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 87.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 10:57:33 | ||
图片预览



文档简介
一次函数的应用
一、选择题
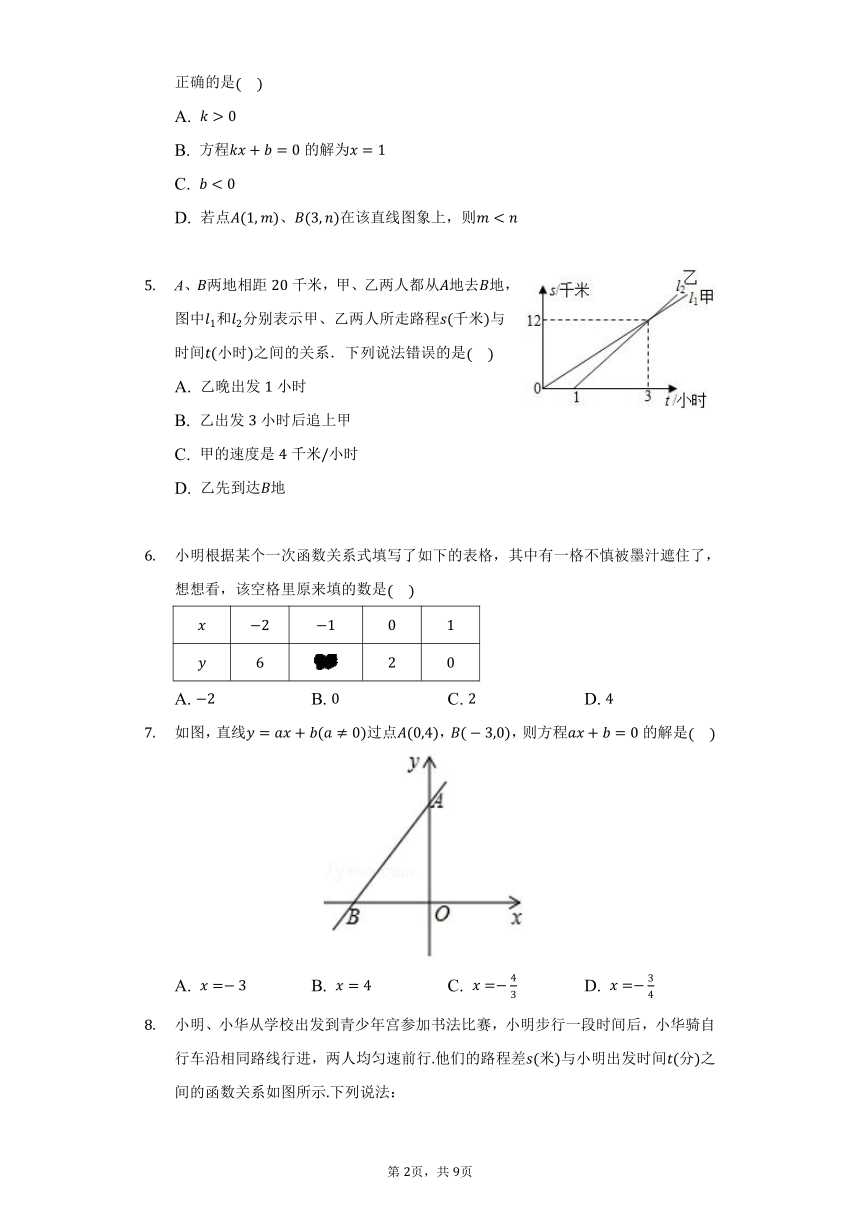
小亮从家出发步行到公交站台后,等公交车去学校,如图,折线表示这个过程中行程千米与所花时间分标之间的关系.下列说法错误的是
A. 他家到公交车站台需行千米
B. 他等公交车的时间为分钟
C. 公交车的速度是米分
D. 他步行与乘公交车行驶的平均速度是米分
甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为小时,两车之间的距离为千米,图中的折线表示与之间的函数关系,下列说法:
甲、乙两地相距千米;
点的实际意义是两车出发后小时相遇;
,;
动车的速度是千米小时.
其中不正确的是
A. B. C. D.
若关于的方程的解为,则直线一定经过点:
A. B. C. D.
如图,直线的图象如图所示.下列结论中,正确的是
A.
B. 方程的解为
C.
D. 若点、在该直线图象上,则
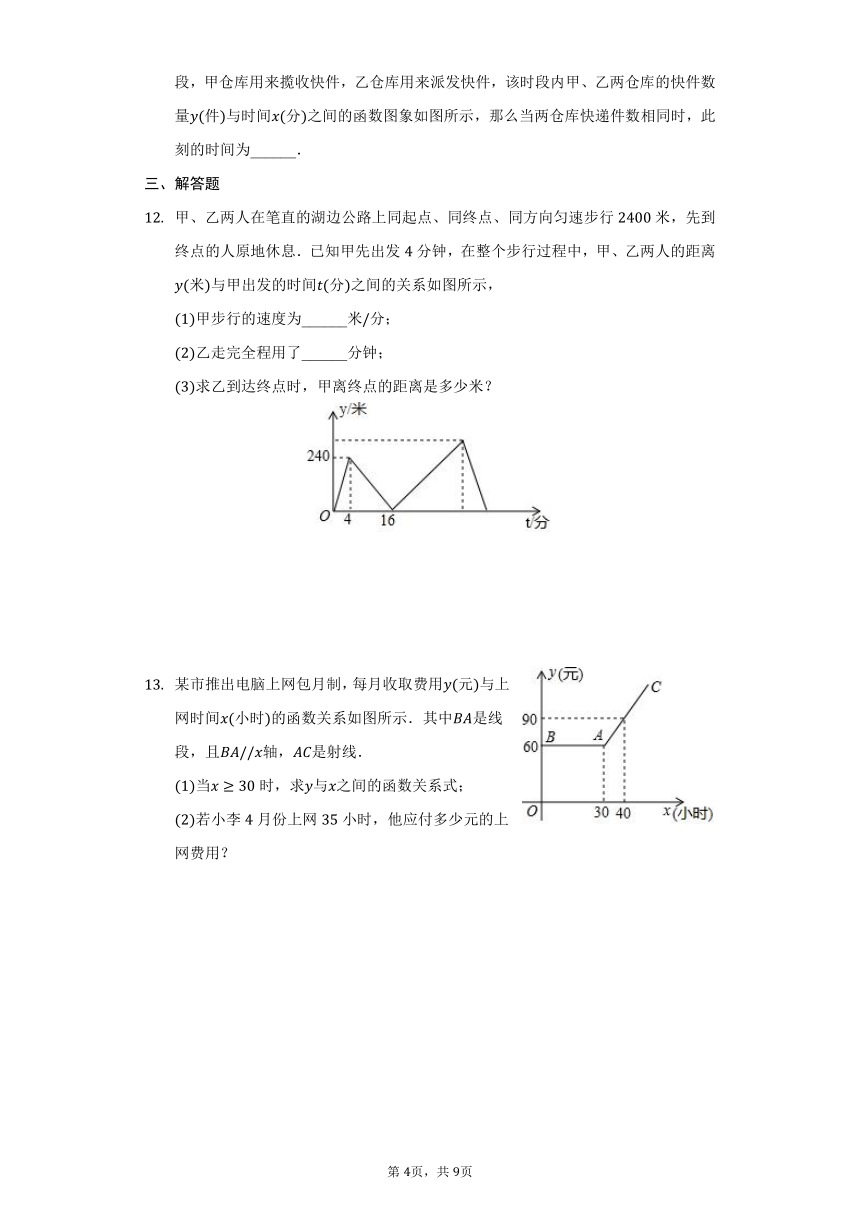
A、两地相距千米,甲、乙两人都从地去地,图中和分别表示甲、乙两人所走路程千米与时间小时之间的关系.下列说法错误的是
A. 乙晚出发小时
B. 乙出发小时后追上甲
C. 甲的速度是千米小时
D. 乙先到达地
小明根据某个一次函数关系式填写了如下的表格,其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是
A. B. C. D.
如图,直线过点,,则方程的解是
A. B. C. D.
小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行他们的路程差米与小明出发时间分之间的函数关系如图所示下列说法:
小华先到达青少年宫;小华的速度是小明速度的倍;;
其中正确的是
A. B. C. D.
二、填空题
,两地相距,甲从地出发向地前进,乙从地出发向地前进,两人沿同一直线同时出发,甲先以的速度前进小时,然后减慢速度继续匀速前进,甲乙两人离地的距离与时间的关系如图所示,则甲出发______小时后与乙相遇.
某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程米与甲出发的时间分钟之间的关系如图所示乙给甲手机的时间忽略不计则乙回到公司时,甲距公司的路程是______米.
某快递公司每天上午::为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量件与时间分之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为______.
三、解答题
甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行米,先到终点的人原地休息.已知甲先出发分钟,在整个步行过程中,甲、乙两人的距离米与甲出发的时间分之间的关系如图所示,
甲步行的速度为______米分;
乙走完全程用了______分钟;
求乙到达终点时,甲离终点的距离是多少米?
某市推出电脑上网包月制,每月收取费用元与上网时间小时的函数关系如图所示.其中是线段,且轴,是射线.
当时,求与之间的函数关系式;
若小李月份上网小时,他应付多少元的上网费用?
答案和解析
1.【答案】
【解析】解:由函数图象可知他家到公交车站台需行千米,他等公交车的时间分钟,故A、B正确,与要求不符;
公交车的速度米分,故C正确,与要求不符;
他步行与乘公交车行驶的平均速度米分,故D错误,与要求相符.
2.【答案】
【解析】解:由图象可知,甲、乙两地相距千米,故说法正确;
点的实际意义是两车出发后小时相遇,故说法正确;
普通列车的速度为:,动车的速度为:,故说法错误;
,
,,
故说法正确;
3.【答案】
【解答】
解:方程的解为,
当时,,
则直线一定经过点,
故选A.
4.【答案】
【解析】解:一次函数的图象过一、二、四象限,
,,
随的增大而减小,
若点、在该直线图象上,则.
故A、、均错误;
直线与轴的交点为,
方程的解是,故B正确.
5.【答案】
【解析】解:由图象可得,
乙晚出发小时,故选项A正确;
乙出发小时追上甲,故选项B错误;
甲的速度是千米小时,故选项C正确;
乙先到达地,故选项D正确;
6.【答案】
【解析】解:设,
由表格可知,一次函数经过点,,
则有,
解得,
,
当时,,
7.【答案】
【解答】
解:方程的解,即为函数图象与轴交点的横坐标,
直线过,
方程的解是,
故选:.
8.【答案】
【解答】
解:由图象得出小明步行米,需要分钟,
所以小明的运动速度为:分,
当第分钟时,小华运动分钟,
运动距离为:,
小华的运动速度为:分,
,故正确;
当第分钟以后两人之间距离越来越近,说明小华已经到达终点,则小华先到达青少年宫,故正确;
此时小华运动分钟,
运动总距离为:,
小明运动时间为:分钟,
故的值为,故错误;
小明分钟运动距离为:,
,故正确.
故正确的有:.
故选A.
9.【答案】
【解析】解:甲减速后的速度为:,
一道速度为:,
设甲出发小时后与乙相遇,根据题意得
,
解得.
即甲出发小时后与乙相遇.
故答案为:.
根据题意结合图象分别求出甲减速后的速度已经乙的速度,再列方程解答即可.
10.【答案】
【解析】解:由题意可得,
甲的速度为:米分,
乙的速度为:米分,
乙从与甲相遇到返回公司用的时间为分钟,
则乙回到公司时,甲距公司的路程是:米,
故答案为:.
11.【答案】:
【解析】解:设甲仓库的快件数量件与时间分之间的函数关系式为:,根据题意得,解得,
;
设乙仓库的快件数量件与时间分之间的函数关系式为:,根据题意得,解得,
,
联立,解得,
此刻的时间为:.
故答案为::.
分别求出甲、乙两仓库的快件数量件与时间分之间的函数关系式,求出两条直线的交点坐标即可.
12.【答案】
【解析】解:由图可得,
甲步行的速度为:米分,
故答案为:;
乙的速度为:米分,
即乙走完全程的时间:分钟,
故答案为:;
米,
13.【答案】解:设当时,与之间的函数关系式是,
,
解得,,
即当时,与之间的函数关系式是;
当时,
,
即小李月份上网小时,他应付元的上网费用.
第2页,共2页
第1页,共1页
一、选择题
小亮从家出发步行到公交站台后,等公交车去学校,如图,折线表示这个过程中行程千米与所花时间分标之间的关系.下列说法错误的是
A. 他家到公交车站台需行千米
B. 他等公交车的时间为分钟
C. 公交车的速度是米分
D. 他步行与乘公交车行驶的平均速度是米分
甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为小时,两车之间的距离为千米,图中的折线表示与之间的函数关系,下列说法:
甲、乙两地相距千米;
点的实际意义是两车出发后小时相遇;
,;
动车的速度是千米小时.
其中不正确的是
A. B. C. D.
若关于的方程的解为,则直线一定经过点:
A. B. C. D.
如图,直线的图象如图所示.下列结论中,正确的是
A.
B. 方程的解为
C.
D. 若点、在该直线图象上,则
A、两地相距千米,甲、乙两人都从地去地,图中和分别表示甲、乙两人所走路程千米与时间小时之间的关系.下列说法错误的是
A. 乙晚出发小时
B. 乙出发小时后追上甲
C. 甲的速度是千米小时
D. 乙先到达地
小明根据某个一次函数关系式填写了如下的表格,其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是
A. B. C. D.
如图,直线过点,,则方程的解是
A. B. C. D.
小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行他们的路程差米与小明出发时间分之间的函数关系如图所示下列说法:
小华先到达青少年宫;小华的速度是小明速度的倍;;
其中正确的是
A. B. C. D.
二、填空题
,两地相距,甲从地出发向地前进,乙从地出发向地前进,两人沿同一直线同时出发,甲先以的速度前进小时,然后减慢速度继续匀速前进,甲乙两人离地的距离与时间的关系如图所示,则甲出发______小时后与乙相遇.
某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程米与甲出发的时间分钟之间的关系如图所示乙给甲手机的时间忽略不计则乙回到公司时,甲距公司的路程是______米.
某快递公司每天上午::为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量件与时间分之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为______.
三、解答题
甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行米,先到终点的人原地休息.已知甲先出发分钟,在整个步行过程中,甲、乙两人的距离米与甲出发的时间分之间的关系如图所示,
甲步行的速度为______米分;
乙走完全程用了______分钟;
求乙到达终点时,甲离终点的距离是多少米?
某市推出电脑上网包月制,每月收取费用元与上网时间小时的函数关系如图所示.其中是线段,且轴,是射线.
当时,求与之间的函数关系式;
若小李月份上网小时,他应付多少元的上网费用?
答案和解析
1.【答案】
【解析】解:由函数图象可知他家到公交车站台需行千米,他等公交车的时间分钟,故A、B正确,与要求不符;
公交车的速度米分,故C正确,与要求不符;
他步行与乘公交车行驶的平均速度米分,故D错误,与要求相符.
2.【答案】
【解析】解:由图象可知,甲、乙两地相距千米,故说法正确;
点的实际意义是两车出发后小时相遇,故说法正确;
普通列车的速度为:,动车的速度为:,故说法错误;
,
,,
故说法正确;
3.【答案】
【解答】
解:方程的解为,
当时,,
则直线一定经过点,
故选A.
4.【答案】
【解析】解:一次函数的图象过一、二、四象限,
,,
随的增大而减小,
若点、在该直线图象上,则.
故A、、均错误;
直线与轴的交点为,
方程的解是,故B正确.
5.【答案】
【解析】解:由图象可得,
乙晚出发小时,故选项A正确;
乙出发小时追上甲,故选项B错误;
甲的速度是千米小时,故选项C正确;
乙先到达地,故选项D正确;
6.【答案】
【解析】解:设,
由表格可知,一次函数经过点,,
则有,
解得,
,
当时,,
7.【答案】
【解答】
解:方程的解,即为函数图象与轴交点的横坐标,
直线过,
方程的解是,
故选:.
8.【答案】
【解答】
解:由图象得出小明步行米,需要分钟,
所以小明的运动速度为:分,
当第分钟时,小华运动分钟,
运动距离为:,
小华的运动速度为:分,
,故正确;
当第分钟以后两人之间距离越来越近,说明小华已经到达终点,则小华先到达青少年宫,故正确;
此时小华运动分钟,
运动总距离为:,
小明运动时间为:分钟,
故的值为,故错误;
小明分钟运动距离为:,
,故正确.
故正确的有:.
故选A.
9.【答案】
【解析】解:甲减速后的速度为:,
一道速度为:,
设甲出发小时后与乙相遇,根据题意得
,
解得.
即甲出发小时后与乙相遇.
故答案为:.
根据题意结合图象分别求出甲减速后的速度已经乙的速度,再列方程解答即可.
10.【答案】
【解析】解:由题意可得,
甲的速度为:米分,
乙的速度为:米分,
乙从与甲相遇到返回公司用的时间为分钟,
则乙回到公司时,甲距公司的路程是:米,
故答案为:.
11.【答案】:
【解析】解:设甲仓库的快件数量件与时间分之间的函数关系式为:,根据题意得,解得,
;
设乙仓库的快件数量件与时间分之间的函数关系式为:,根据题意得,解得,
,
联立,解得,
此刻的时间为:.
故答案为::.
分别求出甲、乙两仓库的快件数量件与时间分之间的函数关系式,求出两条直线的交点坐标即可.
12.【答案】
【解析】解:由图可得,
甲步行的速度为:米分,
故答案为:;
乙的速度为:米分,
即乙走完全程的时间:分钟,
故答案为:;
米,
13.【答案】解:设当时,与之间的函数关系式是,
,
解得,,
即当时,与之间的函数关系式是;
当时,
,
即小李月份上网小时,他应付元的上网费用.
第2页,共2页
第1页,共1页
