2.5 二次函数与一元二次方程(第二课时) 课件(共15张PPT)
文档属性
| 名称 | 2.5 二次函数与一元二次方程(第二课时) 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 11:29:08 | ||
图片预览





文档简介
(共15张PPT)
第二章 二次函数
第 二章 二次函数
5 二次函数与一元二次方程
第2课时
学 习 目 标
1、利用二次函数的图象求一元二次方程近似解.(重点)
2、经历探索用二次函数图象求解一元二次方程近似解的过程,体会用二次函数函数图象求一元二次方程解的方法.(难点)
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
两个相异的实根
b2-4ac > 0
有一个交点
两个相等的实根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
知识回顾
1 、若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数y=ax2+bx+c的图象与x轴交点坐标是 。
(-2,0)和(3,0)
2 、抛物线y=0.5x2-x+3与x轴的交点情况是( )
A 两个交点 B 一个交点
C 没有交点 D 画出图象后才能说明
c
3、不画图象,求抛物线y=x2-x-6与x轴交点坐标。
抛物线y=x2-6x+4与x轴交点坐标为:
(-2,0)和(3,0)
课前训练
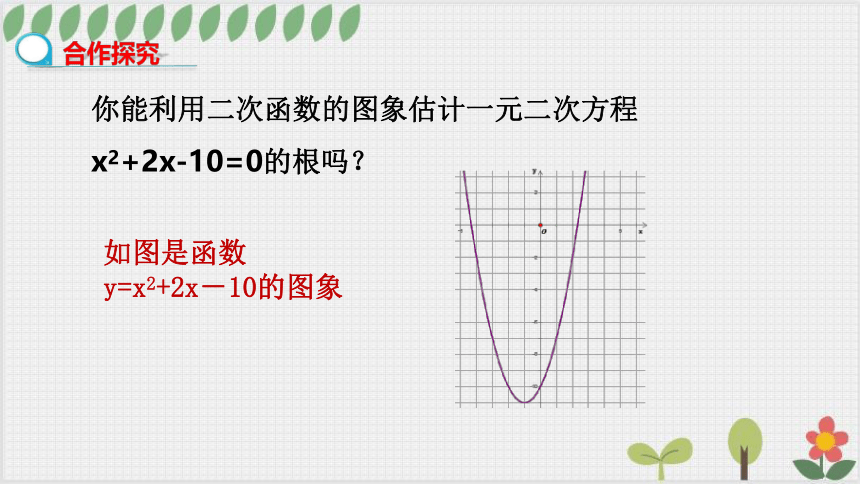
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
如图是函数
y=x2+2x-10的图象
合作探究
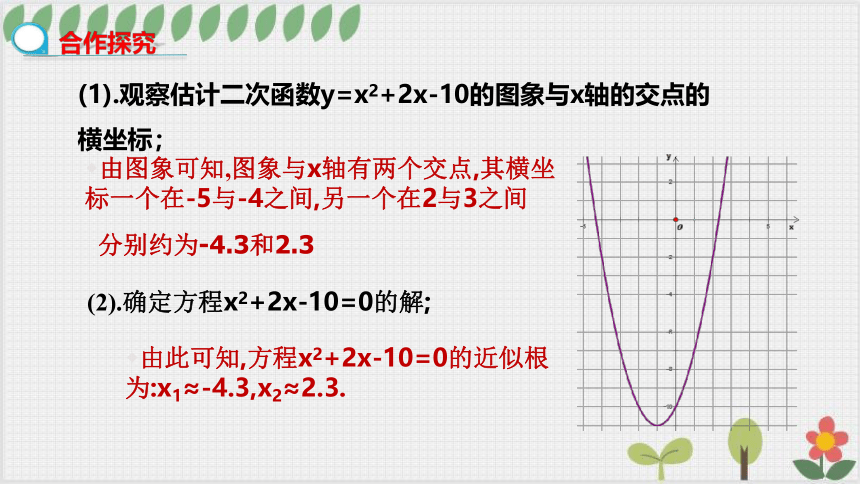
(1).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间
(2).确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
分别约为-4.3和2.3
合作探究
用一元二次方程的求根公式验证一下,看是否有相同的结果
你认为利用二次函数的图象求一元二次方程的近似根的时候,应该注意什么?
小组交流
(1).用描点法作二次函数y=x2+2x-10的图象;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(2). 作直线y=3;
做一做
(3).观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
(4).确定方程x2+2x-10=3的解;
由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(1).原方程可变形为x2+2x-13=0;
(3).观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7
(4).确定方程x2+2x-10=3的解;
方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2). 作二次函数y=x2+2x-13的图象;
解法2
利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=0的近似根的一般步骤是怎样的?
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解。
课堂小结
二次函数y=-2x2+4x+1的图象如图所示,求一元二次方程-2x2+4x+1=0的近似根.
方程-2x2+4x+1=0的近似根为:x1≈-0.2,x2≈2.2.
课堂练习
如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是
y=-x2+2x+3(x﹥0)。柱子OA的高度是多少米?若不计其它因素,水池的半径至少为多少米,才能使喷出的水流不至于落在池外?
拓展应用
解: 在y=-x2+2x+3中,当x=0时y=3,
∴ OA=3m
而当y=0时,x1=-1(舍去),x2=3
∴水池的半径至少为3m.
第二章 二次函数
第 二章 二次函数
5 二次函数与一元二次方程
第2课时
学 习 目 标
1、利用二次函数的图象求一元二次方程近似解.(重点)
2、经历探索用二次函数图象求解一元二次方程近似解的过程,体会用二次函数函数图象求一元二次方程解的方法.(难点)
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
两个相异的实根
b2-4ac > 0
有一个交点
两个相等的实根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
知识回顾
1 、若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数y=ax2+bx+c的图象与x轴交点坐标是 。
(-2,0)和(3,0)
2 、抛物线y=0.5x2-x+3与x轴的交点情况是( )
A 两个交点 B 一个交点
C 没有交点 D 画出图象后才能说明
c
3、不画图象,求抛物线y=x2-x-6与x轴交点坐标。
抛物线y=x2-6x+4与x轴交点坐标为:
(-2,0)和(3,0)
课前训练
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
如图是函数
y=x2+2x-10的图象
合作探究
(1).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间
(2).确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
分别约为-4.3和2.3
合作探究
用一元二次方程的求根公式验证一下,看是否有相同的结果
你认为利用二次函数的图象求一元二次方程的近似根的时候,应该注意什么?
小组交流
(1).用描点法作二次函数y=x2+2x-10的图象;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(2). 作直线y=3;
做一做
(3).观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).
(4).确定方程x2+2x-10=3的解;
由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(1).原方程可变形为x2+2x-13=0;
(3).观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7
(4).确定方程x2+2x-10=3的解;
方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2). 作二次函数y=x2+2x-13的图象;
解法2
利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=0的近似根的一般步骤是怎样的?
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解。
课堂小结
二次函数y=-2x2+4x+1的图象如图所示,求一元二次方程-2x2+4x+1=0的近似根.
方程-2x2+4x+1=0的近似根为:x1≈-0.2,x2≈2.2.
课堂练习
如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是
y=-x2+2x+3(x﹥0)。柱子OA的高度是多少米?若不计其它因素,水池的半径至少为多少米,才能使喷出的水流不至于落在池外?
拓展应用
解: 在y=-x2+2x+3中,当x=0时y=3,
∴ OA=3m
而当y=0时,x1=-1(舍去),x2=3
∴水池的半径至少为3m.
