3.4 圆周角和圆心角的关系(第1课时) 课件(共22张PPT)
文档属性
| 名称 | 3.4 圆周角和圆心角的关系(第1课时) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 12:31:30 | ||
图片预览





文档简介
(共22张PPT)
第 三章 圆
第三章 圆
3.4 圆周角和圆心角的关系 (第1课时)
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
如图,在足球射门的游戏中,球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠BAC)有关.当球员在B、D、E三点射门时,他所处的位置对球门AC分别形成三个张角∠BAC,∠BAC,∠BAC.这三个角的大小有什么关系?在这三点射门的效果一样吗?
情景导入
知识讲解
问题:指出图中的圆心角,你知道∠BAC是什么角吗?
A
B
C
O
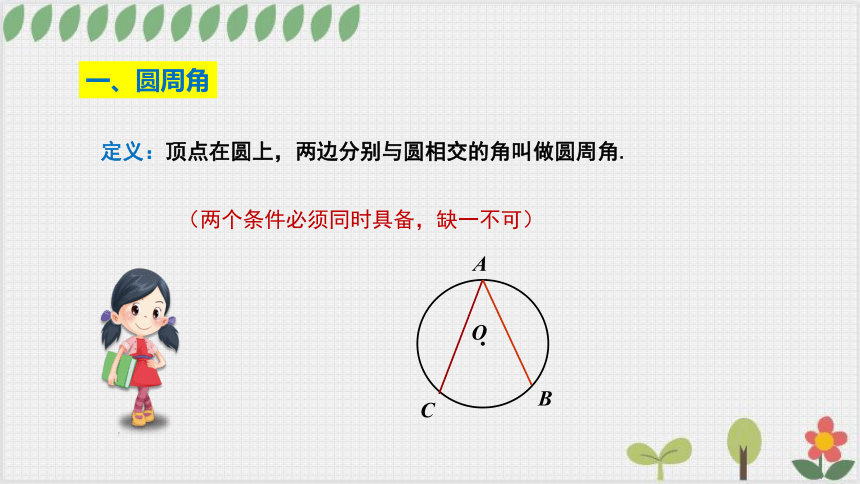
一、圆周角
定义:顶点在圆上,两边分别与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
A
B
C
O
顶点在圆内
顶点在圆外
圆周角
圆心角
·
C
O
A
B
C
O
B
C
A
B
A
B
C
O
A
B
C
O
B
A
A
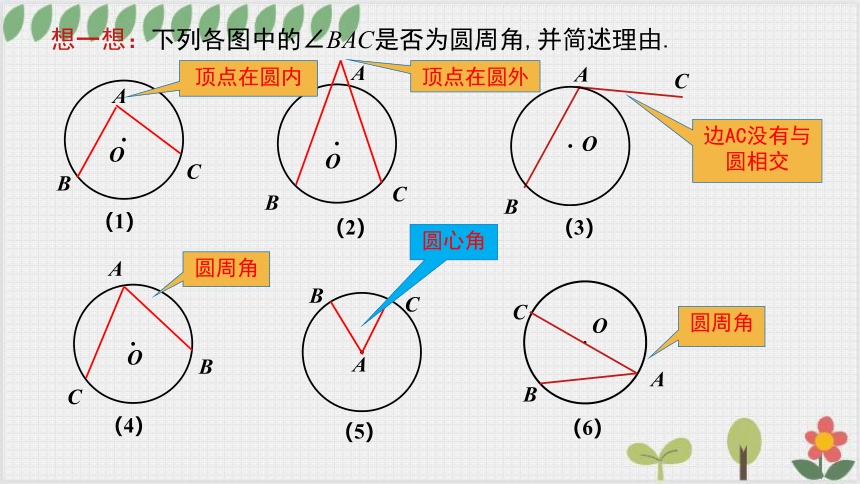
想一想:下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
C
(4)
边AC没有与圆相交
圆周角
O
活动1: 圆周角与圆心角的关系
做一做:
如图,∠AOB=80°.
(1)请你画几个 所对的圆周角?这几个圆周角有什么关系?与同伴进行交流.
(2)这些圆周角和圆心角∠AOB的大小有什么关系?你是怎么发现的?与同伴进行交流.
D
E
F
∠D=∠E= ∠F=40°
合作探究
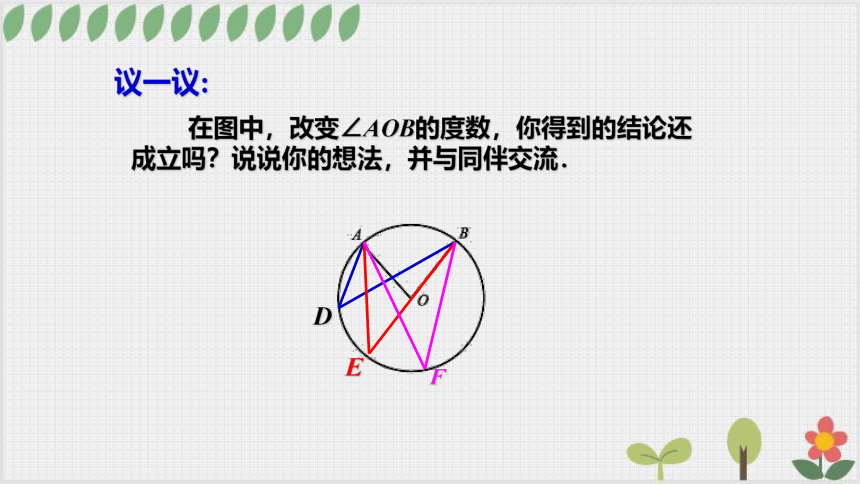
在图中,改变∠AOB的度数,你得到的结论还成立吗?说说你的想法,并与同伴交流.
议一议:
D
E
F
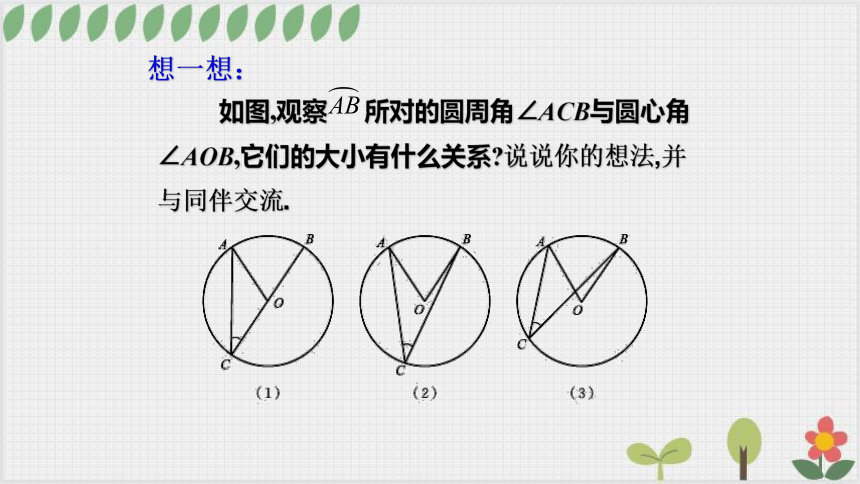
如图,观察 所对的圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系 说说你的想法,并与同伴交流.
想一想:
已知:如图,∠C是 所对的圆周角,∠AOB是 所对的圆心角.
求证: ∠C= ∠AOB .
分析:根据圆周角和圆心角的位置关系,分三种情况讨论:
(1)圆心O在圆周角∠C的一边上,如图(1);
(2)圆心O在圆周角∠C的内部,如图(2);
(3)圆心O在圆周角∠C的外部,如图(3).
证明:(1)当圆心O在圆周角∠C的一边上时,如图(1).
∵∠AOB是△ACO的外角,
∴∠AOB=∠C+∠A.
∵OA=OC,
∴∠A=∠C.
∴∠AOB=2∠C,
.
你能将图(2)、(3)转化成图(1)吗?与同伴交流,并尝试证明.
试一试:
二、圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
(1)如图,在直径为AB的半圆中,O为圆心,C,D为半圆上的两点,∠COD=50°,则∠CAD=_______.
第(1)题 第(2)题
(2)如图,A、B、C为⊙O上三点,∠ABO=65°,求∠BCA的度数.
25°
25°
学以致用
(1)在足球射门的游戏中,球员在B、D、E三点射门时,所形成的三个张角∠BAC,∠BAC,∠BAC大小有什么关系?你能用圆周角定理证明你的结论吗?
拓展延伸
(2)如图,在⊙O中 = ,那么∠C和∠G的大小有什么关系 为什么
O
F
B
A
C
E
G
推论:同弧或等弧所对的圆周角相等
1.判断题:
(1)在同圆或等圆中等弧所对的圆周角相等. ( )
(2)相等的圆周角所对的弧也相等. ( )
(3)同弦所对的圆周角相等. ( )
2.在如图所示的8个角中,哪些是相等的角?你能从图中找出几对相似三角形吗?
√
×
×
∠1=∠4,∠2=∠7,
∠3=∠6,∠5=∠8,
△AEB∽△DEC
△AED∽△BEC
跟踪训练
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
3.圆周角定理推论:同弧(或等弧)所对的圆周角相等
.
课堂小结
O
A
B
C
(第1题) (第2题) (第3题)
1.如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于 .
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为 .
3.如图,弦AB与CD相交于点P,
求证:PA PB=PC PD
30°
30°
随堂检测
连接AC,BD.
∵∠BAC=∠CDB,
∠ACD=∠DBA,
∴△PAC∽△PDB.
即 PA PB=PC PD
C
B
A
D
P
证明:
O
A
B
C
1
2
4.如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC.
∠1= ∠2有什么大小关系?请说明理由?
第 三章 圆
第三章 圆
3.4 圆周角和圆心角的关系 (第1课时)
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的
关系”.(难点)
如图,在足球射门的游戏中,球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠BAC)有关.当球员在B、D、E三点射门时,他所处的位置对球门AC分别形成三个张角∠BAC,∠BAC,∠BAC.这三个角的大小有什么关系?在这三点射门的效果一样吗?
情景导入
知识讲解
问题:指出图中的圆心角,你知道∠BAC是什么角吗?
A
B
C
O
一、圆周角
定义:顶点在圆上,两边分别与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
A
B
C
O
顶点在圆内
顶点在圆外
圆周角
圆心角
·
C
O
A
B
C
O
B
C
A
B
A
B
C
O
A
B
C
O
B
A
A
想一想:下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
C
(4)
边AC没有与圆相交
圆周角
O
活动1: 圆周角与圆心角的关系
做一做:
如图,∠AOB=80°.
(1)请你画几个 所对的圆周角?这几个圆周角有什么关系?与同伴进行交流.
(2)这些圆周角和圆心角∠AOB的大小有什么关系?你是怎么发现的?与同伴进行交流.
D
E
F
∠D=∠E= ∠F=40°
合作探究
在图中,改变∠AOB的度数,你得到的结论还成立吗?说说你的想法,并与同伴交流.
议一议:
D
E
F
如图,观察 所对的圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系 说说你的想法,并与同伴交流.
想一想:
已知:如图,∠C是 所对的圆周角,∠AOB是 所对的圆心角.
求证: ∠C= ∠AOB .
分析:根据圆周角和圆心角的位置关系,分三种情况讨论:
(1)圆心O在圆周角∠C的一边上,如图(1);
(2)圆心O在圆周角∠C的内部,如图(2);
(3)圆心O在圆周角∠C的外部,如图(3).
证明:(1)当圆心O在圆周角∠C的一边上时,如图(1).
∵∠AOB是△ACO的外角,
∴∠AOB=∠C+∠A.
∵OA=OC,
∴∠A=∠C.
∴∠AOB=2∠C,
.
你能将图(2)、(3)转化成图(1)吗?与同伴交流,并尝试证明.
试一试:
二、圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
(1)如图,在直径为AB的半圆中,O为圆心,C,D为半圆上的两点,∠COD=50°,则∠CAD=_______.
第(1)题 第(2)题
(2)如图,A、B、C为⊙O上三点,∠ABO=65°,求∠BCA的度数.
25°
25°
学以致用
(1)在足球射门的游戏中,球员在B、D、E三点射门时,所形成的三个张角∠BAC,∠BAC,∠BAC大小有什么关系?你能用圆周角定理证明你的结论吗?
拓展延伸
(2)如图,在⊙O中 = ,那么∠C和∠G的大小有什么关系 为什么
O
F
B
A
C
E
G
推论:同弧或等弧所对的圆周角相等
1.判断题:
(1)在同圆或等圆中等弧所对的圆周角相等. ( )
(2)相等的圆周角所对的弧也相等. ( )
(3)同弦所对的圆周角相等. ( )
2.在如图所示的8个角中,哪些是相等的角?你能从图中找出几对相似三角形吗?
√
×
×
∠1=∠4,∠2=∠7,
∠3=∠6,∠5=∠8,
△AEB∽△DEC
△AED∽△BEC
跟踪训练
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
3.圆周角定理推论:同弧(或等弧)所对的圆周角相等
.
课堂小结
O
A
B
C
(第1题) (第2题) (第3题)
1.如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于 .
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为 .
3.如图,弦AB与CD相交于点P,
求证:PA PB=PC PD
30°
30°
随堂检测
连接AC,BD.
∵∠BAC=∠CDB,
∠ACD=∠DBA,
∴△PAC∽△PDB.
即 PA PB=PC PD
C
B
A
D
P
证明:
O
A
B
C
1
2
4.如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC.
∠1= ∠2有什么大小关系?请说明理由?
