3.6 直线和圆的位置关系(第一课时) 课件(共17张PPT)
文档属性
| 名称 | 3.6 直线和圆的位置关系(第一课时) 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 10:18:24 | ||
图片预览





文档简介
(共17张PPT)
第 三章 圆
第三章 圆
3.6 直线和圆的位置关系
(第1课时)
学习目标
1.经历探索直线和圆位置关系的过程.
2.理解直线与圆有相交、相切、相离三种位置关系.(重点)
3.了解切线的概念,探索切线与过切点的直径之间的关系.(难点)
如图,如果我们把太阳看作一个圆,把地平线看作一条直线,太阳升起的过程中,太阳和地平线会有几种位置关系?
情景导入
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
●O
●O
●O
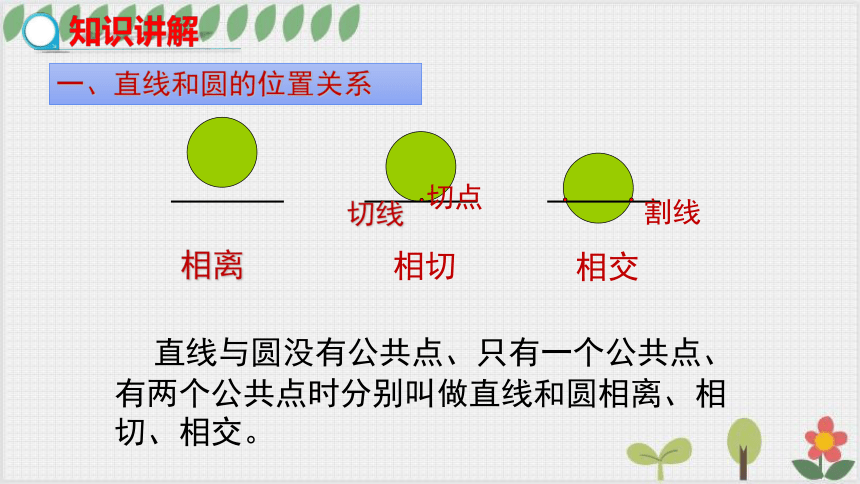
直线与圆没有公共点、只有一个公共点、有两个公共点时分别叫做直线和圆相离、相切、相交。
相离
相交
相切
切点
切线
割线
知识讲解
一、直线和圆的位置关系
(2)直线l和⊙O相切
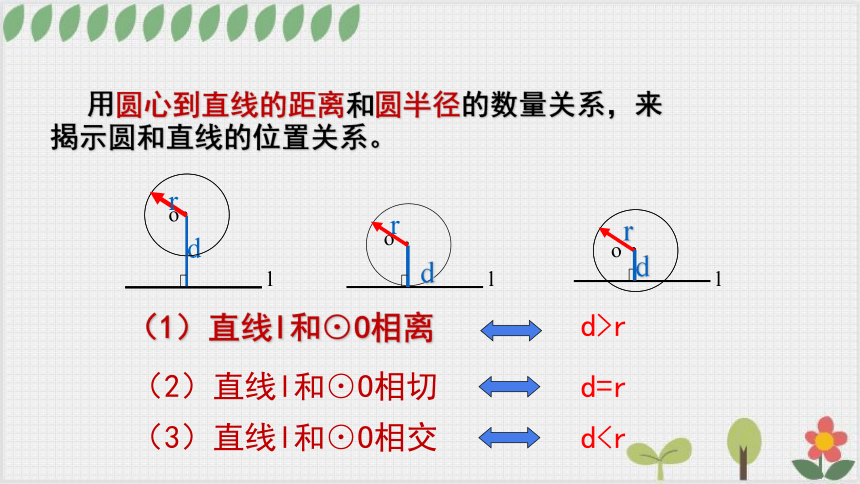
用圆心到直线的距离和圆半径的数量关系,来揭示圆和直线的位置关系。
(1)直线l和⊙O相离
(3)直线l和⊙O相交
d>r
d=r
dd
o
r
l
d
o
r
l
o
d
r
l
判定直线与圆的位置关系
的方法有____种:
总结:
(1)根据定义,由直线与圆的公共点的个数来判断;
(2)根据性质,由圆心到直线的距离d与半径r 的关系来判断.
两
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
相交
相切
相离
2
1
0
练一练
(3)若AB和⊙O相交,则
2、已知:⊙O的半径为5,圆心O与直线AB的距离为d, 根据条件填写d的范围:
(1)若AB和⊙O相离, 则
(2)若AB和⊙O相切, 则
d > 5
d = 5
d < 5
0≤
例1:在Rt△ABC中∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的关系? (1) r=2cm (2) r=2.4cm (3) r=3cm
D
D
D
A
B
C
A
B
C
A
B
C
例题讲解
如图,已知∠AOB= 30°,M为OB上一点,且OM=5,若以M为圆心,r为半径作圆,根据下列条件写出半径r的取值范围:
1)当直线OA与⊙M相离时, 2)当直线OA与⊙M相切时, 3)当直线OA与⊙M有公共点时,
C
O
0< r < 2.5
r = 2.5
r≥2.5
30°
M
B
A
5
跟踪训练
┐
相切时:观察过切点的半径OA与切线AD有何关系?
●O
A
●
D
二、圆的切线的性质
思考 如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
直径AB垂直于直线CD.
理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.
C
D
B
●O
A
切线性质定理:
圆的切线垂直于过切点的半径.
┐
●
A
●
D
O
几何语言
∵CD切⊙O于A,
∴CD⊥OA.
C
1.已知⊙O的直径等于12cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为( )
A.0 B.1 C.2 D.无法确定
C
3. 已知⊙O半径R=3,O点到l的距离为d,且d是方程
X2-5X+6=0的一个根,则l与⊙O的位置关系是 。
.
2. 已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是( )
B
.
.
.
.
A
B
C
D
l
l
l
l
O
O
O
O
相切或相交
随堂训练
本节课你学到了哪些知识?
(1)直线和圆的位置关系:相离、相切和相交.
① 从公共点的个数来判断 ——“形”
② 从d与r的数量关系来判断——“数”
(2)直线和圆的位置关系的性质与判定:
d >r 直线 l 和⊙O 相离;
d =r 直线 l 和⊙O 相切;
d <r 直线 l 和⊙O 相交.
(3)圆的切线垂直于过切点的半径.
课堂小结
第 三章 圆
第三章 圆
3.6 直线和圆的位置关系
(第1课时)
学习目标
1.经历探索直线和圆位置关系的过程.
2.理解直线与圆有相交、相切、相离三种位置关系.(重点)
3.了解切线的概念,探索切线与过切点的直径之间的关系.(难点)
如图,如果我们把太阳看作一个圆,把地平线看作一条直线,太阳升起的过程中,太阳和地平线会有几种位置关系?
情景导入
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
●O
●O
●O
直线与圆没有公共点、只有一个公共点、有两个公共点时分别叫做直线和圆相离、相切、相交。
相离
相交
相切
切点
切线
割线
知识讲解
一、直线和圆的位置关系
(2)直线l和⊙O相切
用圆心到直线的距离和圆半径的数量关系,来揭示圆和直线的位置关系。
(1)直线l和⊙O相离
(3)直线l和⊙O相交
d>r
d=r
d
o
r
l
d
o
r
l
o
d
r
l
判定直线与圆的位置关系
的方法有____种:
总结:
(1)根据定义,由直线与圆的公共点的个数来判断;
(2)根据性质,由圆心到直线的距离d与半径r 的关系来判断.
两
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
相交
相切
相离
2
1
0
练一练
(3)若AB和⊙O相交,则
2、已知:⊙O的半径为5,圆心O与直线AB的距离为d, 根据条件填写d的范围:
(1)若AB和⊙O相离, 则
(2)若AB和⊙O相切, 则
d > 5
d = 5
d < 5
0≤
例1:在Rt△ABC中∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的关系? (1) r=2cm (2) r=2.4cm (3) r=3cm
D
D
D
A
B
C
A
B
C
A
B
C
例题讲解
如图,已知∠AOB= 30°,M为OB上一点,且OM=5,若以M为圆心,r为半径作圆,根据下列条件写出半径r的取值范围:
1)当直线OA与⊙M相离时, 2)当直线OA与⊙M相切时, 3)当直线OA与⊙M有公共点时,
C
O
0< r < 2.5
r = 2.5
r≥2.5
30°
M
B
A
5
跟踪训练
┐
相切时:观察过切点的半径OA与切线AD有何关系?
●O
A
●
D
二、圆的切线的性质
思考 如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
直径AB垂直于直线CD.
理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.
C
D
B
●O
A
切线性质定理:
圆的切线垂直于过切点的半径.
┐
●
A
●
D
O
几何语言
∵CD切⊙O于A,
∴CD⊥OA.
C
1.已知⊙O的直径等于12cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为( )
A.0 B.1 C.2 D.无法确定
C
3. 已知⊙O半径R=3,O点到l的距离为d,且d是方程
X2-5X+6=0的一个根,则l与⊙O的位置关系是 。
.
2. 已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是( )
B
.
.
.
.
A
B
C
D
l
l
l
l
O
O
O
O
相切或相交
随堂训练
本节课你学到了哪些知识?
(1)直线和圆的位置关系:相离、相切和相交.
① 从公共点的个数来判断 ——“形”
② 从d与r的数量关系来判断——“数”
(2)直线和圆的位置关系的性质与判定:
d >r 直线 l 和⊙O 相离;
d =r 直线 l 和⊙O 相切;
d <r 直线 l 和⊙O 相交.
(3)圆的切线垂直于过切点的半径.
课堂小结
