3.7 切线长定理 课件(共19张PPT)
文档属性
| 名称 | 3.7 切线长定理 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第三章 圆
第三章 圆
3.7 切线长定理
学习目标
1.掌握切线长定理,初步学会运用切线长定理进 行计算与证明.(重点)
2.了解三角形的内切圆和三角形的内心的概念.
3.学会利用方程思想解决几何问题,体验数形结合思想.(难点)
新课导入
P
O
O.
P
B
A
A
B
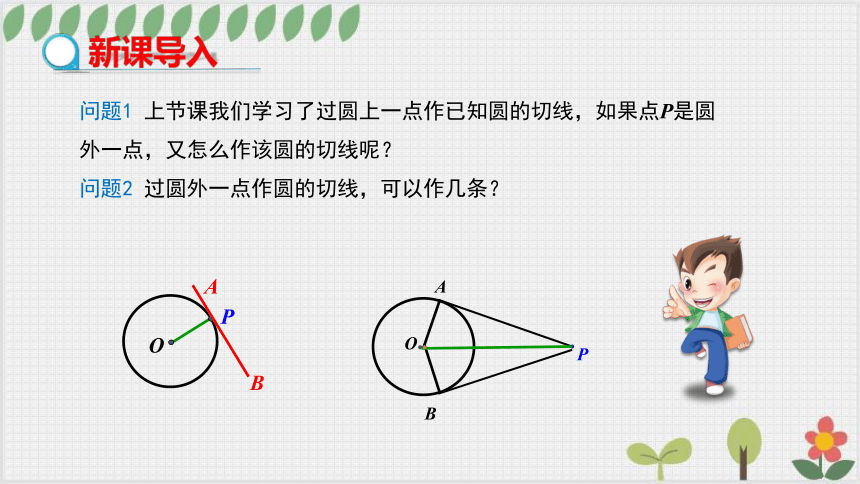
问题1 上节课我们学习了过圆上一点作已知圆的切线,如果点P是圆外一点,又怎么作该圆的切线呢?
问题2 过圆外一点作圆的切线,可以作几条?
一、切线长
知识讲解
P
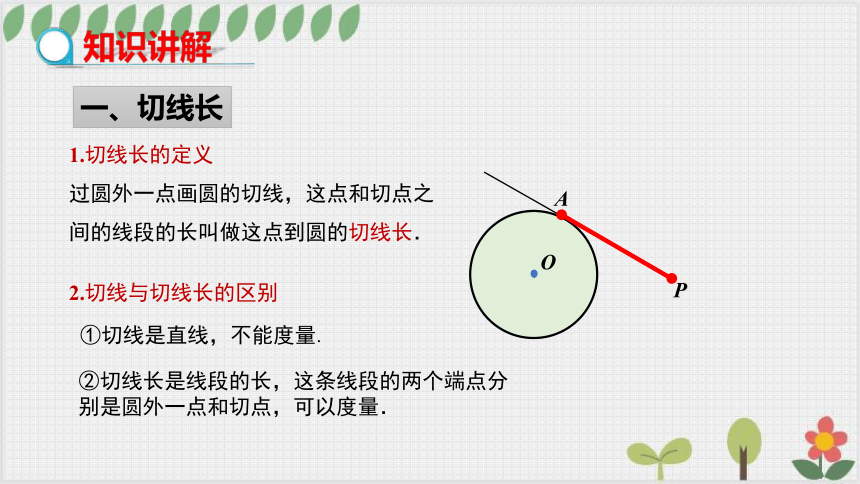
1.切线长的定义
过圆外一点画圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线与切线长的区别
二、切线长定理
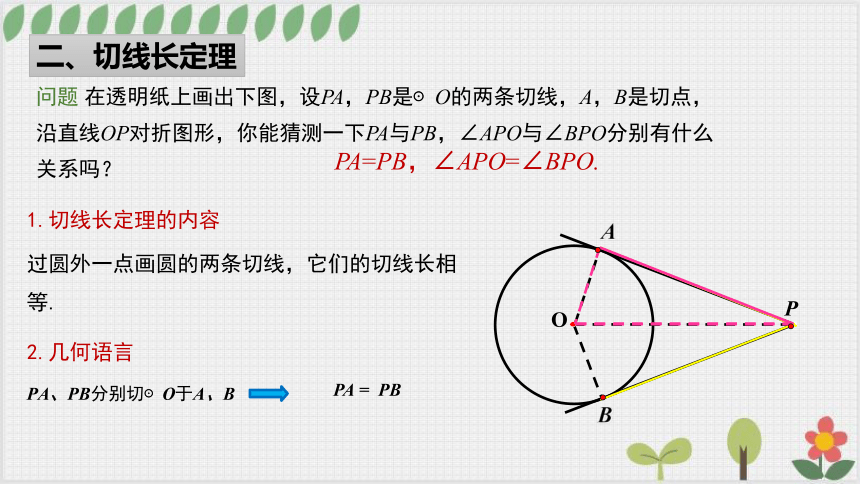
问题 在透明纸上画出下图,设PA,PB是⊙O的两条切线,A,B是切点,沿直线OP对折图形,你能猜测一下PA与PB,∠APO与∠BPO分别有什么关系吗?
PA=PB,∠APO=∠BPO.
1.切线长定理的内容
过圆外一点画圆的两条切线,它们的切线长相等.
PA、PB分别切⊙O于A、B
PA = PB
2.几何语言
B
P
O
A
拓展结论
PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于点C.
(1)写出图中所有的垂直关系;
OA⊥PA,OB ⊥PB,AB ⊥OP.
(3)写出图中所有的全等三角形;
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.
(4)写出图中所有的等腰三角形.
△APB △AOB
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC.
B
P
O
A
C
E
D
★切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
三、三角形的内切圆及内心
问题: 如何作圆,使它和已知三角形的各边都相切?
已知:△ABC.
求作:和△ABC的各边都相切的圆.
M
N
D
作法:
(1)作∠B和∠C的平分线BM和CN,交点为O.
(2)过点O作OD⊥BC, 垂足为D.
(3)以点O为圆心,OD为半径作圆O.
⊙O就是所求作的圆.
A
C
B
1.与三角形各边都相切的圆叫做三角形的内切圆.
B
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角平分线的交点.
┐
A
C
O
┐
┐
D
E
F
提示:三角形的内心到三角形的三边的距离相等.
⊙O是△ABC的内切圆,
点O是△ABC的内心,△ABC是⊙O的外切三角形,
OD=OE=OF.
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
垂直平分线的交点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条
角平分线的
交点
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
外心与内心的区别:
A
B
O
A
B
C
O
C
例1:已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求⊙O 的半径。
O
C
B
A
E
D
F
变式1:△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
【解析】
设AF=x,则AE=x
∴CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.
由BD+CD=BC可得
13-x+9-x=14,
解得x=4.
∴ AF=4 cm, BD=5 cm, CE=9 cm.
变式2 已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=12cm,求△PEF的周长.
【解析】易证EQ=EA, FQ=FB,PA=PB.
∴ PE+EQ=PA=12cm,
PF+FQ=PB=PA=12cm.
∴周长为24cm.
F
A
B
D
L
M
N
P
O
结论:圆的外切四边形的两组对边和相等。
已知:四边形ABCD的边 AB,BC,CD,DA和圆O分别相切于L,M,N,P。
C
(1)找出图中所有相等的线段
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
想一想
探索圆外切四边形边的关系
课堂小结
切线长
切线长定理
作用
图形的轴对称性
依据
提供了证线段和
角相等的方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
三角形内切圆
运用切线长定理,将相等线段转化到某条边上,从而建立方程,求线段的长.
有关概念
内心、三角形的内切圆、圆的外切三角形
应用
重要结论
只适合于直角三角形
当堂检测
20 °
4
B
P
O
A
第2题
1.如图,PA切⊙O于点A,PB切⊙O于点B,下列结论中,错误的是( )
A.∠APO =∠BPO B.PA = PB
C.AB ⊥OP D.PA = P0
D
B
P
O
A
第1题
2.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如AP=4, ∠APB = 40 ° ,则∠APO = , PB = .
3.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= .
65 °或115 °
B
P
O
A
第3题
4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3, BD+CE=12, 则△ABC的周长是 .
A
B
C
F
E
D
O
第4题
24
5.如图,在△ABC 中,∠ABC=50 ,∠ACB=75 ,点O是△ ABC的内心,求∠BOC的度数.
解:∵点O是△ABC 的内心,
∴∠OBC = ∠ABC = ×50 = 25 ,
∠OCB = ∠ACB = ×75 =37.5 .
在△OBC 中,∠BOC =180 - ∠OBC - ∠OCB
=180 - 25 - 37.5 = 117.5 .
6.△ABC的内切圆半径为r,△ABC的周长为,求△ABC的面积. (提示:设内心为O,连接OA、OB、OC)
解:如图, 设三个切点分别为D,E,F.
连接OD, OE, OF.
= + +
= ×AB×r+ ×BC×r+ ×AC×r
= ×(AB +BC +AC )×r
= r
┐
A
C
O
┐
┐
D
E
F
B
第三章 圆
第三章 圆
3.7 切线长定理
学习目标
1.掌握切线长定理,初步学会运用切线长定理进 行计算与证明.(重点)
2.了解三角形的内切圆和三角形的内心的概念.
3.学会利用方程思想解决几何问题,体验数形结合思想.(难点)
新课导入
P
O
O.
P
B
A
A
B
问题1 上节课我们学习了过圆上一点作已知圆的切线,如果点P是圆外一点,又怎么作该圆的切线呢?
问题2 过圆外一点作圆的切线,可以作几条?
一、切线长
知识讲解
P
1.切线长的定义
过圆外一点画圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线与切线长的区别
二、切线长定理
问题 在透明纸上画出下图,设PA,PB是⊙O的两条切线,A,B是切点,沿直线OP对折图形,你能猜测一下PA与PB,∠APO与∠BPO分别有什么关系吗?
PA=PB,∠APO=∠BPO.
1.切线长定理的内容
过圆外一点画圆的两条切线,它们的切线长相等.
PA、PB分别切⊙O于A、B
PA = PB
2.几何语言
B
P
O
A
拓展结论
PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于点C.
(1)写出图中所有的垂直关系;
OA⊥PA,OB ⊥PB,AB ⊥OP.
(3)写出图中所有的全等三角形;
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.
(4)写出图中所有的等腰三角形.
△APB △AOB
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC.
B
P
O
A
C
E
D
★切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
三、三角形的内切圆及内心
问题: 如何作圆,使它和已知三角形的各边都相切?
已知:△ABC.
求作:和△ABC的各边都相切的圆.
M
N
D
作法:
(1)作∠B和∠C的平分线BM和CN,交点为O.
(2)过点O作OD⊥BC, 垂足为D.
(3)以点O为圆心,OD为半径作圆O.
⊙O就是所求作的圆.
A
C
B
1.与三角形各边都相切的圆叫做三角形的内切圆.
B
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角平分线的交点.
┐
A
C
O
┐
┐
D
E
F
提示:三角形的内心到三角形的三边的距离相等.
⊙O是△ABC的内切圆,
点O是△ABC的内心,△ABC是⊙O的外切三角形,
OD=OE=OF.
名称 确定方法 图形 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
垂直平分线的交点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条
角平分线的
交点
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
外心与内心的区别:
A
B
O
A
B
C
O
C
例1:已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求⊙O 的半径。
O
C
B
A
E
D
F
变式1:△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
【解析】
设AF=x,则AE=x
∴CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.
由BD+CD=BC可得
13-x+9-x=14,
解得x=4.
∴ AF=4 cm, BD=5 cm, CE=9 cm.
变式2 已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=12cm,求△PEF的周长.
【解析】易证EQ=EA, FQ=FB,PA=PB.
∴ PE+EQ=PA=12cm,
PF+FQ=PB=PA=12cm.
∴周长为24cm.
F
A
B
D
L
M
N
P
O
结论:圆的外切四边形的两组对边和相等。
已知:四边形ABCD的边 AB,BC,CD,DA和圆O分别相切于L,M,N,P。
C
(1)找出图中所有相等的线段
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
想一想
探索圆外切四边形边的关系
课堂小结
切线长
切线长定理
作用
图形的轴对称性
依据
提供了证线段和
角相等的方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
三角形内切圆
运用切线长定理,将相等线段转化到某条边上,从而建立方程,求线段的长.
有关概念
内心、三角形的内切圆、圆的外切三角形
应用
重要结论
只适合于直角三角形
当堂检测
20 °
4
B
P
O
A
第2题
1.如图,PA切⊙O于点A,PB切⊙O于点B,下列结论中,错误的是( )
A.∠APO =∠BPO B.PA = PB
C.AB ⊥OP D.PA = P0
D
B
P
O
A
第1题
2.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如AP=4, ∠APB = 40 ° ,则∠APO = , PB = .
3.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= .
65 °或115 °
B
P
O
A
第3题
4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3, BD+CE=12, 则△ABC的周长是 .
A
B
C
F
E
D
O
第4题
24
5.如图,在△ABC 中,∠ABC=50 ,∠ACB=75 ,点O是△ ABC的内心,求∠BOC的度数.
解:∵点O是△ABC 的内心,
∴∠OBC = ∠ABC = ×50 = 25 ,
∠OCB = ∠ACB = ×75 =37.5 .
在△OBC 中,∠BOC =180 - ∠OBC - ∠OCB
=180 - 25 - 37.5 = 117.5 .
6.△ABC的内切圆半径为r,△ABC的周长为,求△ABC的面积. (提示:设内心为O,连接OA、OB、OC)
解:如图, 设三个切点分别为D,E,F.
连接OD, OE, OF.
= + +
= ×AB×r+ ×BC×r+ ×AC×r
= ×(AB +BC +AC )×r
= r
┐
A
C
O
┐
┐
D
E
F
B
