1.2 30°,45°,60°角的三角函数值 课件(共15张PPT)
文档属性
| 名称 | 1.2 30°,45°,60°角的三角函数值 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 696.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 10:07:06 | ||
图片预览






文档简介
(共15张PPT)
第一章 直角三角形的边角关系
2. 30°,45°,60°角的三角函数值
第一章 直角三角形的边角关系
1.经历探索 30°, 45°,60°角的三角函数值的过程,能够进行有关推理,进一步体会三角函数的意义,并熟记特殊角的三角函数值。(重点)
2.能够进行含有30°, 45°,60°角的三角函数值的计算。(难点)
3.能利用30°、45°、60°角的三角函数值解决实际问题。
学习目标
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin30°等于多少
(2)cos30°等于多少
(3)tan30°等于多少
请与同伴交流你是怎么想的 又是怎么做的
不仿设两个三角形最短的边长为单位1,易得:
┌
┌
30°
60°
45°
45°
新课导入
(5)sin450,sin600等于多少
(6)cos450,cos600等于多少
(7)tan450,tan600等于多少
┌
┌
300
600
450
450
新课导入
特殊角的三角函数值表
要能记住有多好
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
这张表还可以看出许多知识之间的内在联系呢
知识讲解
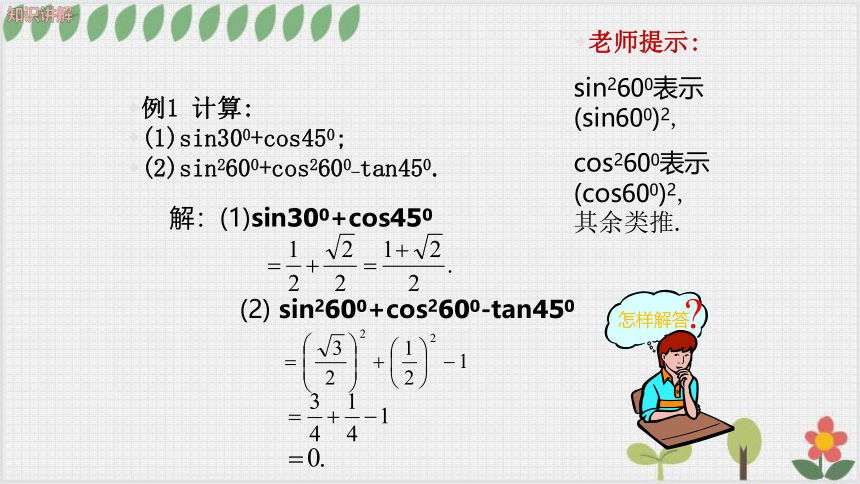
例1 计算:
(1)sin300+cos450;
(2)sin2600+cos2600_tan450.
老师提示:
sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
怎样解答
解:(1)sin300+cos450
(2) sin2600+cos2600-tan450
知识讲解
(1)sin600-cos450;
(2)cos600+tan600;
计算:
练一练
知识讲解
例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
典例解析
知识讲解
∴最高位置与最低位置的高度差约为0.34m.
A
C
O
B
D
┌
解:如图,根据题意可知,
∴AC=OA-OC=2.5-2.165≈0.34(m).
●
2.5
知识讲解
1.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少
14m
跟踪训练
变形应用:
2.如图,在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1
b
A
B
C
a
┌
c
跟踪训练
3.如图,在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别是a,b,c.
求证:
b
A
B
C
a
┌
c
跟踪训练
同角之间的三角函数的关系
平方关系:
b
A
B
C
a
┌
c
商的关系:
知识拓展
直角三角形中的边角关系
看图说话:
直角三角形三边的关系:
a2+b2=c2.
直角三角形两锐角的关系:
∠A+∠B=900.
直角三角形边与角之间的关系:
特殊角300,450,600角的三角函数值:
互余两角之间的三角函数关系:
同角之间的三角函数关系:
b
A
B
C
a
┌
c
┌
┌
300
600
450
450
课堂小结
第一章 直角三角形的边角关系
2. 30°,45°,60°角的三角函数值
第一章 直角三角形的边角关系
1.经历探索 30°, 45°,60°角的三角函数值的过程,能够进行有关推理,进一步体会三角函数的意义,并熟记特殊角的三角函数值。(重点)
2.能够进行含有30°, 45°,60°角的三角函数值的计算。(难点)
3.能利用30°、45°、60°角的三角函数值解决实际问题。
学习目标
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin30°等于多少
(2)cos30°等于多少
(3)tan30°等于多少
请与同伴交流你是怎么想的 又是怎么做的
不仿设两个三角形最短的边长为单位1,易得:
┌
┌
30°
60°
45°
45°
新课导入
(5)sin450,sin600等于多少
(6)cos450,cos600等于多少
(7)tan450,tan600等于多少
┌
┌
300
600
450
450
新课导入
特殊角的三角函数值表
要能记住有多好
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
这张表还可以看出许多知识之间的内在联系呢
知识讲解
例1 计算:
(1)sin300+cos450;
(2)sin2600+cos2600_tan450.
老师提示:
sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
怎样解答
解:(1)sin300+cos450
(2) sin2600+cos2600-tan450
知识讲解
(1)sin600-cos450;
(2)cos600+tan600;
计算:
练一练
知识讲解
例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
典例解析
知识讲解
∴最高位置与最低位置的高度差约为0.34m.
A
C
O
B
D
┌
解:如图,根据题意可知,
∴AC=OA-OC=2.5-2.165≈0.34(m).
●
2.5
知识讲解
1.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少
14m
跟踪训练
变形应用:
2.如图,在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1
b
A
B
C
a
┌
c
跟踪训练
3.如图,在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别是a,b,c.
求证:
b
A
B
C
a
┌
c
跟踪训练
同角之间的三角函数的关系
平方关系:
b
A
B
C
a
┌
c
商的关系:
知识拓展
直角三角形中的边角关系
看图说话:
直角三角形三边的关系:
a2+b2=c2.
直角三角形两锐角的关系:
∠A+∠B=900.
直角三角形边与角之间的关系:
特殊角300,450,600角的三角函数值:
互余两角之间的三角函数关系:
同角之间的三角函数关系:
b
A
B
C
a
┌
c
┌
┌
300
600
450
450
课堂小结
