2021--20222学年人教版数学八年级上册11.3.2 多边形的内角和与外角和课件(共39张PPT)
文档属性
| 名称 | 2021--20222学年人教版数学八年级上册11.3.2 多边形的内角和与外角和课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 440.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 00:00:00 | ||
图片预览







文档简介
(共39张PPT)
11.3.2 多边形的内角和与外角和
八年级上册
学习目标
1、了解多边形内角和与外角和的探究过程。
2、掌握多边形内角和与外角和定理。
3、提高学生运用数学的能力和了解转化的数学思想。
学习重难点
重点
难点
理解多边形内角含义,多边形内角和公式。
多边形内角和公式的探索过程;利用多边形内角和公式解决实际问题。
1.多边形的内角和公式是怎样的?
2.多边形的外角和是多少?
3.推导多边形的内角和公式是怎样做的?
思考
你还记得三角形内角和是多少度?
(三角形内角和是180°)
你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
(都是360°)
Why
多边形的内角和
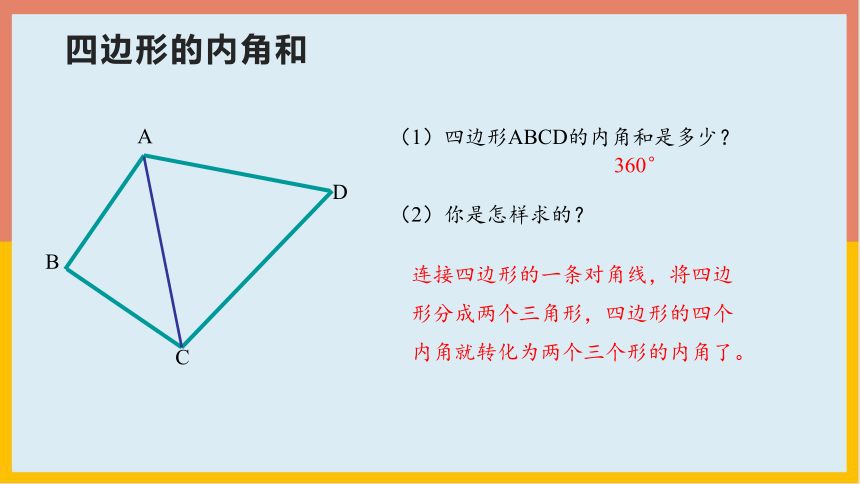
B
A
D
C
(1)四边形ABCD的内角和是多少?
(2)你是怎样求的?
360°
连接四边形的一条对角线,将四边形分成两个三角形,四边形的四个内角就转化为两个三个形的内角了。
四边形的内角和
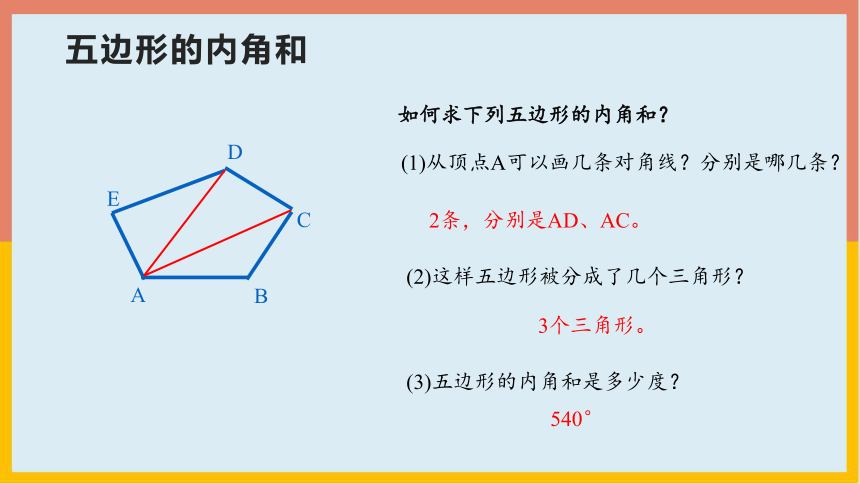
(1)从顶点A可以画几条对角线?分别是哪几条?
(2)这样五边形被分成了几个三角形?
(3)五边形的内角和是多少度?
A
B
D
C
E
如何求下列五边形的内角和?
2条,分别是AD、AC。
3个三角形。
540°
五边形的内角和
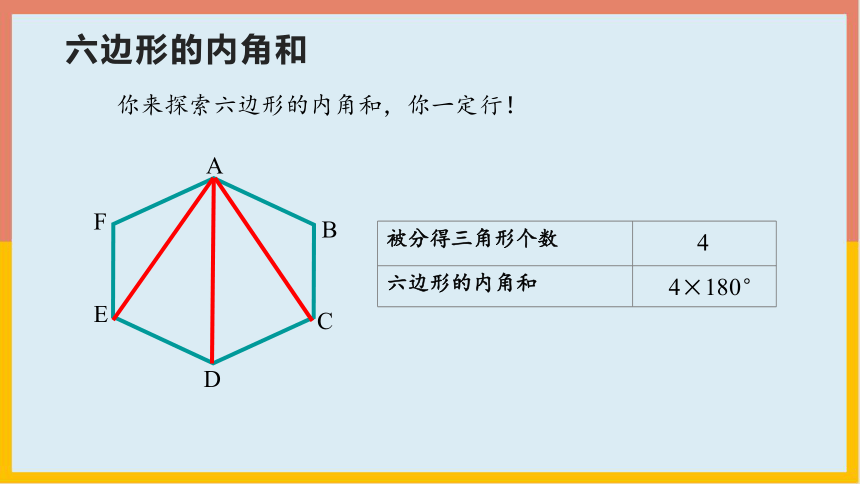
你来探索六边形的内角和,你一定行!
A
B
C
D
被分得三角形个数
六边形的内角和
4
4×180°
E
F
六边形的内角和
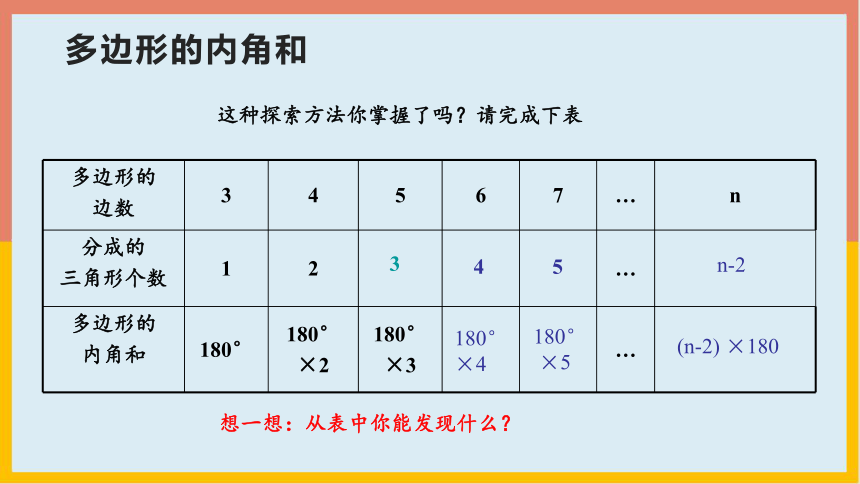
这种探索方法你掌握了吗?请完成下表
多边形的 边数 3 4 5 6 7 … n
分成的 三角形个数 1 2 …
多边形的 内角和 180° 180° ×2 180° ×3 …
3
4
5
n-2
180°
×5
(n-2) ×180
180°
×4
想一想:从表中你能发现什么?
多边形的内角和
多边形内角和公式:
n边形的内角和等于 (n-2).180°
从n边形的一个顶点出发可以引 条对角线,这些对角线把n边形分成 个三角形,内角和为 .
(n-3)
(n-2)
(n-2)x180°
多边形的内角和
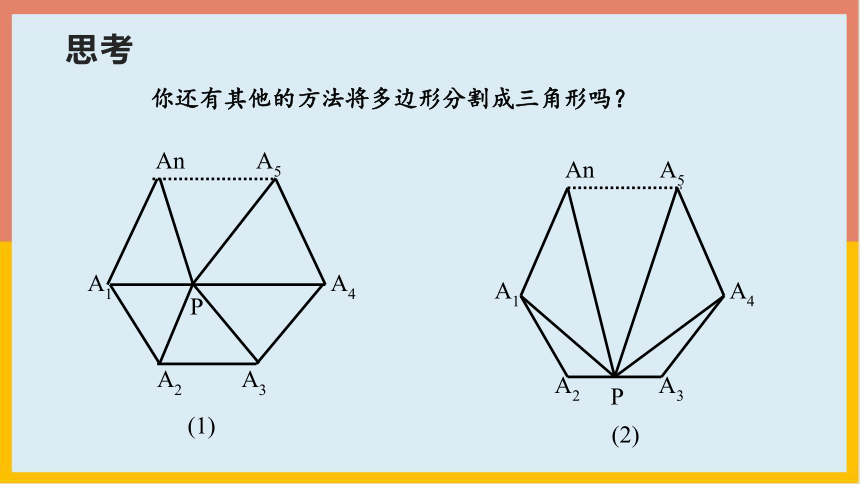
你还有其他的方法将多边形分割成三角形吗?
An A5
A1 A4
A2 A3
P
(1)
A2 A3
P
(2)
An A5
A1 A4
思考
你还有其他的方法将多边形分割成三角形吗?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为(n-1)×180 °- 180 °= (n-2)×180 °
思考
例1 已知四边形ABCD,∠A+∠C=180°,求∠B+∠D.
A
B
C
D
解:四边形的内角和为:
(4-2) ×180 =360°,
∠A+∠C=180°,
所以∠B+∠D= 360°- (∠A+∠C)=180°.
例题讲解
2、已知一个多边形每个内角都等108°,求这个多边形的边数?
解:设这个多边形的边数为 n,
根据题意得:(n-2) ×180=108n
解得:n=5
答:这个多边形是五边形.
1、八边形的内角和等于多少度?十边形呢?
(8-2) ×180°= 1080°
(10-2) ×180°= 1440°
针对训练
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
多边形的外角和
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?
你是怎样得到的?
360°
360°
在多边形的每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
A
B
C
D
E
1
2
3
4
5
多边形的外角和
(1)我们知道三角形的外角和为360°,四边形的外角和等于多少度?
(2)五边形的外角和怎么求?n边形呢?
∠α+∠β+∠γ+∠δ=180°×4-(4-2)×180°=360°
五边形外角和
=五个平角
-五边形内角和
=5×180°
-(5-2) × 180°
=360°.
五边形的外角和等于360°.
多边形的外角和
n边形的外角和是多少度呢
解:都是360°.
因为多边形的外角与它相邻的内角是邻补角,
所以n边形的外角和加内角和等于n·180°,
内角和为(n-2)·180°,
因此,外角和为:n·180°-(n-2)·180°=360°.
结论:任意多边形的外角和都等于360°. 即n边形的外角和为360°.
多边形的外角和
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
例题讲解
1、快速抢答,熟悉公式:
(1)8边形的内角和是 。
(2)一个多边形的内角和是1440°它是 边形。
(3)正五边形的每一个外角等于 .每一个内角等于_____。
(4)如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
1080°
10
72°
108°
12
课堂练习
2、在四边形ABCD中,∠A=120度,∠B:∠C:∠D= 3:4:5,求∠B= ,∠C = , ∠D = 。
3、如果一个四边形的一组对角互补,那么另一组对角的关系是 。
4、正n边形的每一个外角等于 .每一个内角等于 。
5、一个多边形的各内角都等于120°,它是 边形。
60°
80°
100°
互补
6
课堂练习
1.如图,点E在AC上,点F在AB上,BE,CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°.求∠C的度数.
应用拓展
解:由三角形外角的性质,
得∠BFC=∠A+∠C,∠BEC=∠A+∠B.
∵∠BFC比∠BEC大20°,
∴(∠A+∠C)-(∠A+∠B)=20°,
即∠C-∠B=20°.
∵∠C=2∠B,∴∠B=20°,∠C=40°.
2.如图,在△ABC中,点D是∠ACB与∠ABC的平分线的交点,BD的延长线交AC于E.
(1)若∠A=70°,求∠BDC的度数;
应用拓展
解:∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°.
∵BD,CD分别为∠ABC,∠ACB的平分线,
∴∠DBC= ∠ABC,∠DCB= ∠ACB.
∴∠ABC+∠ACB=2(∠DBC+∠DCB)=110°.
∴∠DBC+∠DCB=55°.
∴∠BDC=180°-(∠DBC+∠DCB)=125°.
(2)若∠EDC=50°,求∠A的度数;
解:∵∠EDC=50°,
∴∠DBC+∠DCB=50°.
∵BD,CD分别为∠ABC,∠ACB的平分线,
∴∠DBC= ∠ABC,∠DCB= ∠ACB.
∴∠ABC+∠ACB=2(∠DBC+∠DCB)=100°.
∴∠A=180°-(∠ABC+∠ACB)=80°.
应用拓展
(3)请直接写出∠A与∠BDC之间的数量关系(不必说明理由).
解:∠BDC=90°+ ∠A
应用拓展
3.探究与发现:如图①,有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE,DF恰好分别经过点B,C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由.
应用拓展
解:∠BDC=∠A+∠ABD+∠ACD.
理由:∵∠BDC+∠DBC+∠DCB=180°,
∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°
∴∠BDC=∠A+∠ABD+∠ACD.
应用:某零件如图②所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格.你能说出其中的道理吗?
应用拓展
解:如图,连接BC.
由上述结论得:
合格零件中∠BDC=∠A+∠ABD+∠ACD=143°,
又∵检验员量得∠BDC=145°≠143°,
∴这个零件不合格.
4.如图,在△ABC中,点P是∠ABC,∠ACB的平分线的交点.
(1)若∠A=80°,求∠BPC的度数.
应用拓展
证明:∵BP,CP分别为∠ABC,∠ACB的平分线,
∴∠PBC+∠PCB= (∠ABC+∠ACB)
= (180°-∠A)= ×(180°-80°)=50°.
∴∠BPC=180°-(∠PBC+∠PCB)=180°-50°=130°.
(2)有位同学在解答(1)后得出∠BPC=90°+ ∠A的规律,你认为正确吗?请给出理由.
解:正确.理由如下:
∵BP,CP分别为∠ABC,∠ACB的平分线,
∴∠PBC+∠PCB= (∠ABC+∠ACB)
= (180°-∠A)=90°- ∠A.
∴∠BPC=180°-(∠PBC+∠PCB)
=180°-(90°- ∠A)=90°+ ∠A.
应用拓展
5.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证∠EAC=∠B;
应用拓展
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠EAD=∠EDA,
∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
(2)若∠B=50°,∠CAD :∠E=1 :3,求∠E的度数.
应用拓展
解:设∠CAD=x,则∠E=3x.
由(1)知∠EAC=∠B=50°,
∴∠EAD=∠EDA=x+50°.
在△EAD中,∵∠E+∠EAD+∠EDA=180°
∴3x+2(x+50°)=180°,
解得x=16°.
∴3x=48°,即∠E=48°.
6.如图,在平面直角坐标系中,线段AB的端点A在y轴上,端点B在x轴上,BF平分∠ABO,并与△ABO的外角∠BAG的平分线AE所在的直线交于点F.
(1)当OA=OB时,求∠F的度数.
应用拓展
解:∵OA=OB,∠AOB=90°,
∴△AOB是等腰直角三角形.
∴∠OAB=∠OBA=45°.∴∠BAG=135°.
∵BF平分∠ABO,AE平分∠BAG,
∴∠ABF= ∠OBA=22.5°,
∠BAE= ∠BAG=67.5°.
∴∠F=∠BAE-∠ABF=45°.
(2)当点A,B分别在y轴的正半轴和x轴的正半轴上移动时,其他条件不变,(1)中结论还成立吗?说说你的理由.
应用拓展
解:(1)中结论仍成立.
理由:∵∠EAB是△ABF的外角,
∴∠EAB=∠F+∠ABF.
∵AE平分∠BAG,
∴∠EAB= ∠GAB.
∵∠GAB=∠AOB+∠ABO,
∴∠EAB= ∠GAB= (∠AOB+∠ABO).
∴ (∠AOB+∠ABO)=∠F+∠ABF,即 ×90°+ ∠ABO=∠F+∠ABF.
∵BF平分∠ABO,
∴∠ABF= ∠ABO.∴∠F= ×90°=45°,
即(1)中结论仍成立.
应用拓展
7.如图,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE所在直线折叠压平,使点A与点N重合.
(1)若∠B=35°,∠C=60°,求∠A的度数;
应用拓展
解:∵∠B=35°,∠C=60°,
∴∠A=180°-∠B-∠C=180°-35°-60°=85°.
(2)若∠A=70°,求∠1+∠2的度数.
应用拓展
解:∵∠A=70°,
∴∠ADE+∠AED=180°-70°=110°.
∵△ABC沿着DE所在直线折叠压平,点A与点N重合,
∴∠NDE=∠ADE,∠NED=∠AED.
∴∠1+∠2=180°-(∠NED+∠AED)+180°-(∠NDE+∠ADE)
=360°-2×110°=140°.
1.n边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法: 转化与化归
多边形 三角形
总结
课后作业
2、 一个多边形除一个内角外其余各内角和1999°,求这个多边形的边数。
1、如果一个多边形减掉一个角后形成的多边形的内角和为1080°,那么原多边形的边数是 。
再 见
11.3.2 多边形的内角和与外角和
八年级上册
学习目标
1、了解多边形内角和与外角和的探究过程。
2、掌握多边形内角和与外角和定理。
3、提高学生运用数学的能力和了解转化的数学思想。
学习重难点
重点
难点
理解多边形内角含义,多边形内角和公式。
多边形内角和公式的探索过程;利用多边形内角和公式解决实际问题。
1.多边形的内角和公式是怎样的?
2.多边形的外角和是多少?
3.推导多边形的内角和公式是怎样做的?
思考
你还记得三角形内角和是多少度?
(三角形内角和是180°)
你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
(都是360°)
Why
多边形的内角和
B
A
D
C
(1)四边形ABCD的内角和是多少?
(2)你是怎样求的?
360°
连接四边形的一条对角线,将四边形分成两个三角形,四边形的四个内角就转化为两个三个形的内角了。
四边形的内角和
(1)从顶点A可以画几条对角线?分别是哪几条?
(2)这样五边形被分成了几个三角形?
(3)五边形的内角和是多少度?
A
B
D
C
E
如何求下列五边形的内角和?
2条,分别是AD、AC。
3个三角形。
540°
五边形的内角和
你来探索六边形的内角和,你一定行!
A
B
C
D
被分得三角形个数
六边形的内角和
4
4×180°
E
F
六边形的内角和
这种探索方法你掌握了吗?请完成下表
多边形的 边数 3 4 5 6 7 … n
分成的 三角形个数 1 2 …
多边形的 内角和 180° 180° ×2 180° ×3 …
3
4
5
n-2
180°
×5
(n-2) ×180
180°
×4
想一想:从表中你能发现什么?
多边形的内角和
多边形内角和公式:
n边形的内角和等于 (n-2).180°
从n边形的一个顶点出发可以引 条对角线,这些对角线把n边形分成 个三角形,内角和为 .
(n-3)
(n-2)
(n-2)x180°
多边形的内角和
你还有其他的方法将多边形分割成三角形吗?
An A5
A1 A4
A2 A3
P
(1)
A2 A3
P
(2)
An A5
A1 A4
思考
你还有其他的方法将多边形分割成三角形吗?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为(n-1)×180 °- 180 °= (n-2)×180 °
思考
例1 已知四边形ABCD,∠A+∠C=180°,求∠B+∠D.
A
B
C
D
解:四边形的内角和为:
(4-2) ×180 =360°,
∠A+∠C=180°,
所以∠B+∠D= 360°- (∠A+∠C)=180°.
例题讲解
2、已知一个多边形每个内角都等108°,求这个多边形的边数?
解:设这个多边形的边数为 n,
根据题意得:(n-2) ×180=108n
解得:n=5
答:这个多边形是五边形.
1、八边形的内角和等于多少度?十边形呢?
(8-2) ×180°= 1080°
(10-2) ×180°= 1440°
针对训练
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
多边形的外角和
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?
你是怎样得到的?
360°
360°
在多边形的每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
A
B
C
D
E
1
2
3
4
5
多边形的外角和
(1)我们知道三角形的外角和为360°,四边形的外角和等于多少度?
(2)五边形的外角和怎么求?n边形呢?
∠α+∠β+∠γ+∠δ=180°×4-(4-2)×180°=360°
五边形外角和
=五个平角
-五边形内角和
=5×180°
-(5-2) × 180°
=360°.
五边形的外角和等于360°.
多边形的外角和
n边形的外角和是多少度呢
解:都是360°.
因为多边形的外角与它相邻的内角是邻补角,
所以n边形的外角和加内角和等于n·180°,
内角和为(n-2)·180°,
因此,外角和为:n·180°-(n-2)·180°=360°.
结论:任意多边形的外角和都等于360°. 即n边形的外角和为360°.
多边形的外角和
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
例题讲解
1、快速抢答,熟悉公式:
(1)8边形的内角和是 。
(2)一个多边形的内角和是1440°它是 边形。
(3)正五边形的每一个外角等于 .每一个内角等于_____。
(4)如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
1080°
10
72°
108°
12
课堂练习
2、在四边形ABCD中,∠A=120度,∠B:∠C:∠D= 3:4:5,求∠B= ,∠C = , ∠D = 。
3、如果一个四边形的一组对角互补,那么另一组对角的关系是 。
4、正n边形的每一个外角等于 .每一个内角等于 。
5、一个多边形的各内角都等于120°,它是 边形。
60°
80°
100°
互补
6
课堂练习
1.如图,点E在AC上,点F在AB上,BE,CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°.求∠C的度数.
应用拓展
解:由三角形外角的性质,
得∠BFC=∠A+∠C,∠BEC=∠A+∠B.
∵∠BFC比∠BEC大20°,
∴(∠A+∠C)-(∠A+∠B)=20°,
即∠C-∠B=20°.
∵∠C=2∠B,∴∠B=20°,∠C=40°.
2.如图,在△ABC中,点D是∠ACB与∠ABC的平分线的交点,BD的延长线交AC于E.
(1)若∠A=70°,求∠BDC的度数;
应用拓展
解:∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°.
∵BD,CD分别为∠ABC,∠ACB的平分线,
∴∠DBC= ∠ABC,∠DCB= ∠ACB.
∴∠ABC+∠ACB=2(∠DBC+∠DCB)=110°.
∴∠DBC+∠DCB=55°.
∴∠BDC=180°-(∠DBC+∠DCB)=125°.
(2)若∠EDC=50°,求∠A的度数;
解:∵∠EDC=50°,
∴∠DBC+∠DCB=50°.
∵BD,CD分别为∠ABC,∠ACB的平分线,
∴∠DBC= ∠ABC,∠DCB= ∠ACB.
∴∠ABC+∠ACB=2(∠DBC+∠DCB)=100°.
∴∠A=180°-(∠ABC+∠ACB)=80°.
应用拓展
(3)请直接写出∠A与∠BDC之间的数量关系(不必说明理由).
解:∠BDC=90°+ ∠A
应用拓展
3.探究与发现:如图①,有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE,DF恰好分别经过点B,C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由.
应用拓展
解:∠BDC=∠A+∠ABD+∠ACD.
理由:∵∠BDC+∠DBC+∠DCB=180°,
∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°
∴∠BDC=∠A+∠ABD+∠ACD.
应用:某零件如图②所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格.你能说出其中的道理吗?
应用拓展
解:如图,连接BC.
由上述结论得:
合格零件中∠BDC=∠A+∠ABD+∠ACD=143°,
又∵检验员量得∠BDC=145°≠143°,
∴这个零件不合格.
4.如图,在△ABC中,点P是∠ABC,∠ACB的平分线的交点.
(1)若∠A=80°,求∠BPC的度数.
应用拓展
证明:∵BP,CP分别为∠ABC,∠ACB的平分线,
∴∠PBC+∠PCB= (∠ABC+∠ACB)
= (180°-∠A)= ×(180°-80°)=50°.
∴∠BPC=180°-(∠PBC+∠PCB)=180°-50°=130°.
(2)有位同学在解答(1)后得出∠BPC=90°+ ∠A的规律,你认为正确吗?请给出理由.
解:正确.理由如下:
∵BP,CP分别为∠ABC,∠ACB的平分线,
∴∠PBC+∠PCB= (∠ABC+∠ACB)
= (180°-∠A)=90°- ∠A.
∴∠BPC=180°-(∠PBC+∠PCB)
=180°-(90°- ∠A)=90°+ ∠A.
应用拓展
5.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证∠EAC=∠B;
应用拓展
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠EAD=∠EDA,
∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
(2)若∠B=50°,∠CAD :∠E=1 :3,求∠E的度数.
应用拓展
解:设∠CAD=x,则∠E=3x.
由(1)知∠EAC=∠B=50°,
∴∠EAD=∠EDA=x+50°.
在△EAD中,∵∠E+∠EAD+∠EDA=180°
∴3x+2(x+50°)=180°,
解得x=16°.
∴3x=48°,即∠E=48°.
6.如图,在平面直角坐标系中,线段AB的端点A在y轴上,端点B在x轴上,BF平分∠ABO,并与△ABO的外角∠BAG的平分线AE所在的直线交于点F.
(1)当OA=OB时,求∠F的度数.
应用拓展
解:∵OA=OB,∠AOB=90°,
∴△AOB是等腰直角三角形.
∴∠OAB=∠OBA=45°.∴∠BAG=135°.
∵BF平分∠ABO,AE平分∠BAG,
∴∠ABF= ∠OBA=22.5°,
∠BAE= ∠BAG=67.5°.
∴∠F=∠BAE-∠ABF=45°.
(2)当点A,B分别在y轴的正半轴和x轴的正半轴上移动时,其他条件不变,(1)中结论还成立吗?说说你的理由.
应用拓展
解:(1)中结论仍成立.
理由:∵∠EAB是△ABF的外角,
∴∠EAB=∠F+∠ABF.
∵AE平分∠BAG,
∴∠EAB= ∠GAB.
∵∠GAB=∠AOB+∠ABO,
∴∠EAB= ∠GAB= (∠AOB+∠ABO).
∴ (∠AOB+∠ABO)=∠F+∠ABF,即 ×90°+ ∠ABO=∠F+∠ABF.
∵BF平分∠ABO,
∴∠ABF= ∠ABO.∴∠F= ×90°=45°,
即(1)中结论仍成立.
应用拓展
7.如图,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE所在直线折叠压平,使点A与点N重合.
(1)若∠B=35°,∠C=60°,求∠A的度数;
应用拓展
解:∵∠B=35°,∠C=60°,
∴∠A=180°-∠B-∠C=180°-35°-60°=85°.
(2)若∠A=70°,求∠1+∠2的度数.
应用拓展
解:∵∠A=70°,
∴∠ADE+∠AED=180°-70°=110°.
∵△ABC沿着DE所在直线折叠压平,点A与点N重合,
∴∠NDE=∠ADE,∠NED=∠AED.
∴∠1+∠2=180°-(∠NED+∠AED)+180°-(∠NDE+∠ADE)
=360°-2×110°=140°.
1.n边形的内角和: (n-2)×180°
2.多边形的外角和是 360°
3.数学思想方法: 转化与化归
多边形 三角形
总结
课后作业
2、 一个多边形除一个内角外其余各内角和1999°,求这个多边形的边数。
1、如果一个多边形减掉一个角后形成的多边形的内角和为1080°,那么原多边形的边数是 。
再 见
