2021-2022学年人教版八年级数学上册13.4最短路径问题课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.4最短路径问题课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 534.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 18:16:18 | ||
图片预览





文档简介
(共16张PPT)
八年级上册
13.4 最短路径问题
1、了解解决最短路径问题的基本策略和基本原理,能将实际问题中的“地点”“河” “桥”等抽象为数学中的“点”“线”,使实际问题数学化;
2、能运用轴对称、平移变化解决简单的最短路径问题,体会几何变化在解决最值问题中的重要作用;
学习目标
3、能运用轴对称、平移变化解决简单的最短路径问题,体会几何变化在解决最值问题中的重要作用.
1.两点之间,_______最短。
2.连接直线外一点与直线上各点的所有线段中_______最短。
3.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的__________________。类似的,轴对称图形的对称轴,是任何一对对应点所连线段的______________ 。
4.平移性质:(1)平移前后图形的形状和大小________。(2)对应点连线______________。
线段
垂线段
垂直平分线
垂直平分线
相同
相等
预习反馈
探究点一
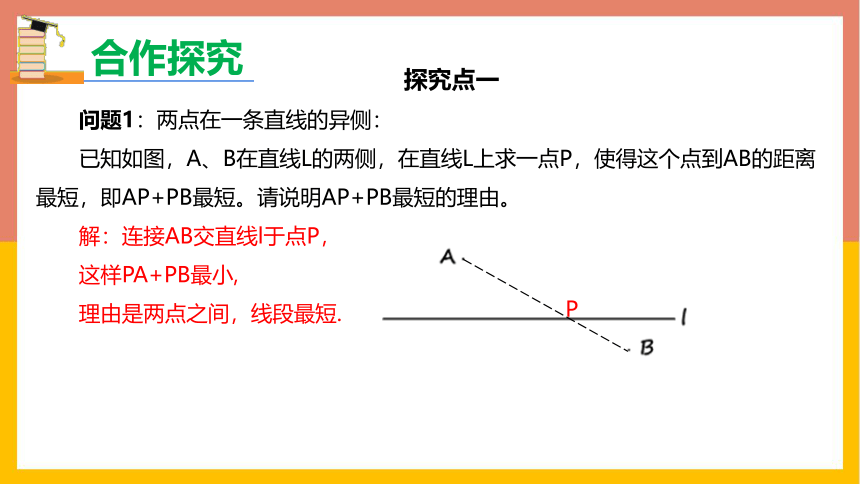
问题1:两点在一条直线的异侧:
已知如图,A、B在直线L的两侧,在直线L上求一点P,使得这个点到AB的距离最短,即AP+PB最短。请说明AP+PB最短的理由。
解:连接AB交直线l于点P,
这样PA+PB最小,
理由是两点之间,线段最短.
P
合作探究
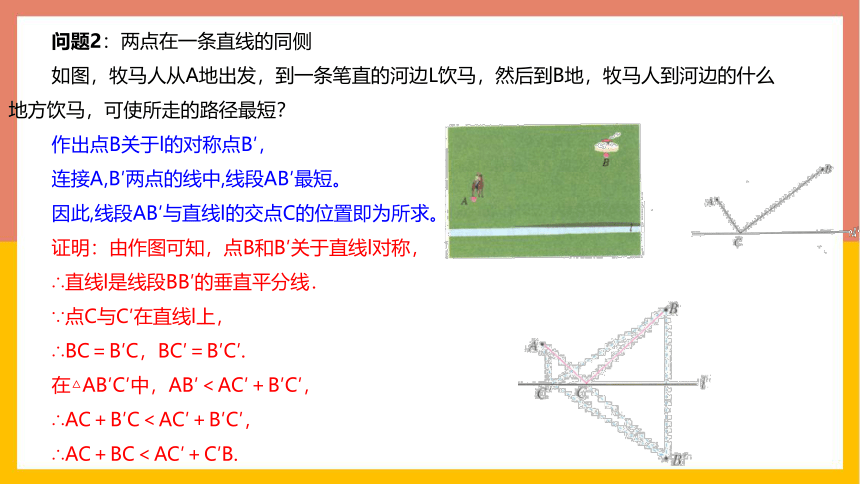
问题2:两点在一条直线的同侧
如图,牧马人从A地出发,到一条笔直的河边L饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
作出点B关于l的对称点B′,
连接A,B′两点的线中,线段AB′最短。
因此,线段AB′与直线l的交点C的位置即为所求。
证明:由作图可知,点B和B′关于直线l对称,
∴直线l是线段BB′的垂直平分线.
∵点C与C′在直线l上,
∴BC=B′C,BC′=B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴AC+B′C<AC′+B′C′,
∴AC+BC<AC′+C′B.
探究点二
问题1:如图,A和B两地在一条河的两岸, 现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直。)
解:(1)如图2,过点A作AC垂直于河岸,且使AC等于河宽.
(2)连接BC与河岸的一边交于点N.
(3)过点N作河岸的垂线交另一条河岸于点M.
则MN为所建的桥的位置.
合作探究
问题2:八(2)班举行文艺晚会,桌子摆成如图所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短?
解:如图.
(1)作C点关于OA的对称点C ,作D点关于OB的对称点D ,
(2)连接C D ,分别交OA,OB于P,Q,那么小明沿C→P→Q→D的路线行走,所走的总路程最短.
1.如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是( )
A.40° B.100° C.140° D.50°
B
随堂检测
2.如图所示,四边形EFGH是一个矩形的台球桌面,有黑白两球分别位于A,B两点,试说明怎样撞 击B,才能使白球先撞击台球桌边EF,反弹后又能击中黑球A
解:先作出点A关于台球边EF的对称点A ,
连接BA 交EF于点O.
将球杆沿BOA 的方向撞击白球,可使白球先撞击台球边EF,然后反弹后又能击中黑球A
A
O
3.如图,点A,B在直线m的同侧,点B′是点B关于m 的对称点,AB′交m于点P.
(1)AB′与AP+BP相等吗?为什么?
(2)在m上再取一点N,并连接AN与BN,比较AN+BN与AP+BP的大小,并说明理由.
解:(1) AB′=AP+BP
点B′是点B关于m 的对称点,
∴BP=B ′P
∴AP+BP=AP+B′P=AB′
(2)在m上再取一点N,并连接AN与BN,
在 ANB ′中,AN+BN >AB ′
故AN+BN>AP+BP
N
4.如图,A和B两地在一 条河的两岸,现要在河上造一座桥MN,使从A到B的路径AM-MN-NB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
D
5.如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5 cm,求∠AOB的度数.
解:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB= ∠COD,
∵PN+PM+MN的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°.
故∠AOB的度数30°.
6.如图,等边△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是 ( )
A
在解决最短路径问题时,我们常利用轴对称、平移等变化把已知问题转化为容易解决的问题,从而作出最短路径的选择。
课堂小结
书面作业:完成相关书本作业
布置作业
再见
八年级上册
13.4 最短路径问题
1、了解解决最短路径问题的基本策略和基本原理,能将实际问题中的“地点”“河” “桥”等抽象为数学中的“点”“线”,使实际问题数学化;
2、能运用轴对称、平移变化解决简单的最短路径问题,体会几何变化在解决最值问题中的重要作用;
学习目标
3、能运用轴对称、平移变化解决简单的最短路径问题,体会几何变化在解决最值问题中的重要作用.
1.两点之间,_______最短。
2.连接直线外一点与直线上各点的所有线段中_______最短。
3.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的__________________。类似的,轴对称图形的对称轴,是任何一对对应点所连线段的______________ 。
4.平移性质:(1)平移前后图形的形状和大小________。(2)对应点连线______________。
线段
垂线段
垂直平分线
垂直平分线
相同
相等
预习反馈
探究点一
问题1:两点在一条直线的异侧:
已知如图,A、B在直线L的两侧,在直线L上求一点P,使得这个点到AB的距离最短,即AP+PB最短。请说明AP+PB最短的理由。
解:连接AB交直线l于点P,
这样PA+PB最小,
理由是两点之间,线段最短.
P
合作探究
问题2:两点在一条直线的同侧
如图,牧马人从A地出发,到一条笔直的河边L饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
作出点B关于l的对称点B′,
连接A,B′两点的线中,线段AB′最短。
因此,线段AB′与直线l的交点C的位置即为所求。
证明:由作图可知,点B和B′关于直线l对称,
∴直线l是线段BB′的垂直平分线.
∵点C与C′在直线l上,
∴BC=B′C,BC′=B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴AC+B′C<AC′+B′C′,
∴AC+BC<AC′+C′B.
探究点二
问题1:如图,A和B两地在一条河的两岸, 现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直。)
解:(1)如图2,过点A作AC垂直于河岸,且使AC等于河宽.
(2)连接BC与河岸的一边交于点N.
(3)过点N作河岸的垂线交另一条河岸于点M.
则MN为所建的桥的位置.
合作探究
问题2:八(2)班举行文艺晚会,桌子摆成如图所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短?
解:如图.
(1)作C点关于OA的对称点C ,作D点关于OB的对称点D ,
(2)连接C D ,分别交OA,OB于P,Q,那么小明沿C→P→Q→D的路线行走,所走的总路程最短.
1.如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是( )
A.40° B.100° C.140° D.50°
B
随堂检测
2.如图所示,四边形EFGH是一个矩形的台球桌面,有黑白两球分别位于A,B两点,试说明怎样撞 击B,才能使白球先撞击台球桌边EF,反弹后又能击中黑球A
解:先作出点A关于台球边EF的对称点A ,
连接BA 交EF于点O.
将球杆沿BOA 的方向撞击白球,可使白球先撞击台球边EF,然后反弹后又能击中黑球A
A
O
3.如图,点A,B在直线m的同侧,点B′是点B关于m 的对称点,AB′交m于点P.
(1)AB′与AP+BP相等吗?为什么?
(2)在m上再取一点N,并连接AN与BN,比较AN+BN与AP+BP的大小,并说明理由.
解:(1) AB′=AP+BP
点B′是点B关于m 的对称点,
∴BP=B ′P
∴AP+BP=AP+B′P=AB′
(2)在m上再取一点N,并连接AN与BN,
在 ANB ′中,AN+BN >AB ′
故AN+BN>AP+BP
N
4.如图,A和B两地在一 条河的两岸,现要在河上造一座桥MN,使从A到B的路径AM-MN-NB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
D
5.如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5 cm,求∠AOB的度数.
解:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB= ∠COD,
∵PN+PM+MN的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°.
故∠AOB的度数30°.
6.如图,等边△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是 ( )
A
在解决最短路径问题时,我们常利用轴对称、平移等变化把已知问题转化为容易解决的问题,从而作出最短路径的选择。
课堂小结
书面作业:完成相关书本作业
布置作业
再见
