2021-2022学年人教版数学八年级上册13.3.2.1等边三角形的性质和判定课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.3.2.1等边三角形的性质和判定课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-21 11:02:17 | ||
图片预览





文档简介
(共27张PPT)
13.3.2.1 等边三角形的性质与判定
八年级上册
学习目标
1、掌握等边三角形的性质.
2、掌握等边三角形的判定方法.
3、会灵活运用性质和判定方法解决实际问题.
学习重难点
重点
难点
等边三角形的性质和判定方法。
会灵活运用性质和判定方法解决实际问题。
下列图片中有你熟悉的数学图形吗?你能说出此图形的名称吗?
导入
等腰三角形
等边三角形
一般三角形
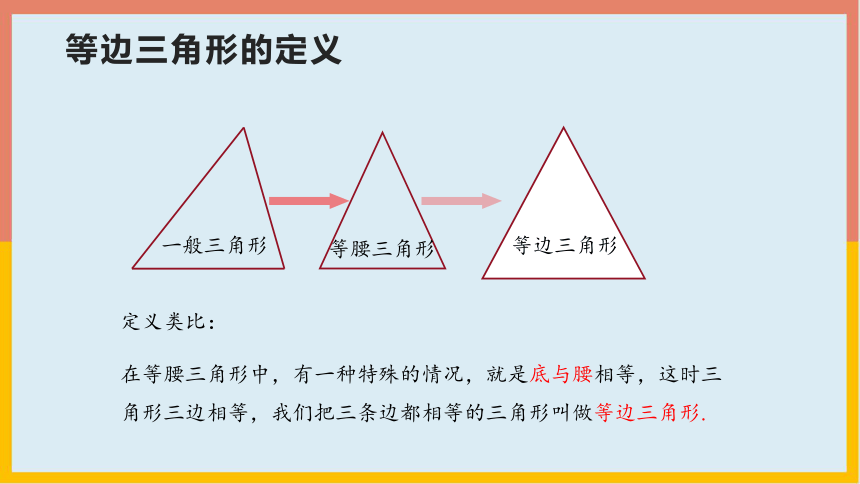
定义类比:
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三条边都相等的三角形叫做等边三角形.
等边三角形的定义
A
B
C
等边三角形是特殊的等腰三角形.
等边三角形的定义
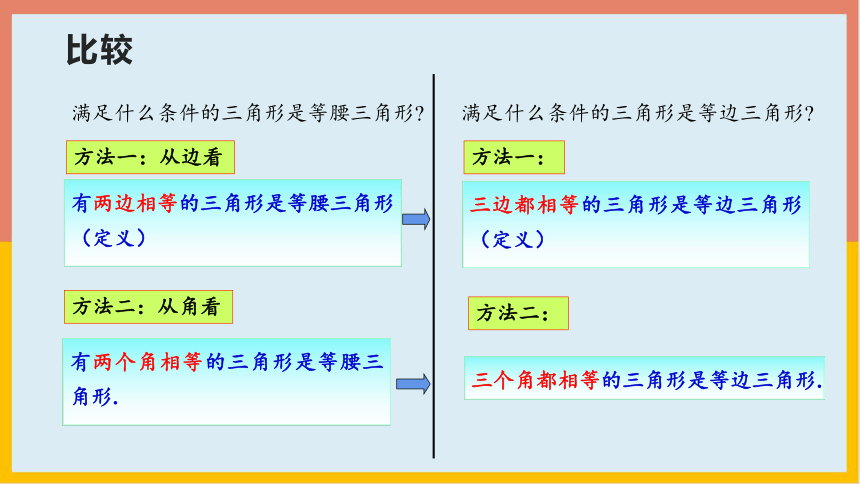
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形
满足什么条件的三角形是等腰三角形
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形.
方法一:从边看
方法二:从角看
方法一:
方法二:
比较
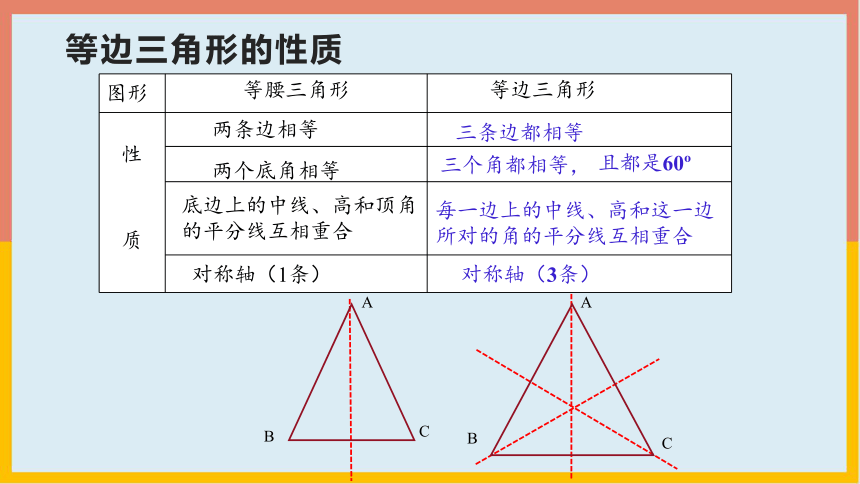
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
A
B
C
A
B
C
等边三角形的性质
A
C
B
D
E
如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.
12
针对训练
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
想一想
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
图形 等腰三角形 判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
∵ ∠A=60°,AB=BC
∴△ABC是等边三角形
等边三角形的判定
例1 如图,△ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点,且DE⊥AC,EF⊥BC,DF⊥AB,计算△DEF各个内角的度数.
解:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°.
∵DE⊥AC,EF⊥BC,DF⊥AB,
∴∠AED=∠EFC=∠FDB=90°,
∴∠ADE=90°-∠A=90°-60°=30°,
∴∠EDF=180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
即△DEF各个内角的度数都是60°.
例题
1.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
D
针对训练
2.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
A.180° B.220° C.240° D.300°
针对训练
C
3.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )
A.3 B.2 C.1 D.0
A
针对训练
例2 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ DE//BC,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
例题
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE, 求证:△ADE是等边三角形.
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ AD=AE,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ADE是等边三角形.
变式训练
例3 如图,已知△ABC是等边三角形,D为边 AC的中点,AE⊥EC,BD=EC,证明:△ADE是等边三角形.
例题
证明:∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=60°,BD⊥AC.
∵AE⊥EC,∴∠BDA=∠CEA=90°.
在Rt△ABD 和Rt△ACE中, AB=AC,
BD=CE,
∴△ABD≌△ACE,
∴AD=AE,∠EAD=∠BAD=60°,
∴△ADE是等边三角形.
例题
1.下列三角形:
①有两个角等于60°的三角形;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有( )
A.①②③ B.①②④
C.①③ D.①②③④
D
针对训练
2.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于 点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
D
针对训练
1.已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为___cm.
9
2.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
课堂练习
B
C
D
A
E
3.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
课堂练习
4.如图,A、O、D三点共线,△OAB和△OCD是两个全等的等边三角形,
求∠AEB的大小.
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A、O、D三点共线,
∴∠DOB=∠COA=120°,
∴△COA ≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
课堂练习
5.如图,已知△ABC是等边三角形,D为边 AC的中点,AE⊥EC,BD=EC,证明:△ADE是等边三角形.
证明:∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=60°,BD⊥AC.
∵AE⊥EC,∴∠BDA=∠CEA=90°.
在Rt△ABD 和Rt△ACE中, AB=AC,
BD=CE,
∴△ABD≌△ACE,∴AD=AE,∠EAD=∠BAD=60°,
∴△ADE是等边三角形.
课堂练习
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
总结
再 见
13.3.2.1 等边三角形的性质与判定
八年级上册
学习目标
1、掌握等边三角形的性质.
2、掌握等边三角形的判定方法.
3、会灵活运用性质和判定方法解决实际问题.
学习重难点
重点
难点
等边三角形的性质和判定方法。
会灵活运用性质和判定方法解决实际问题。
下列图片中有你熟悉的数学图形吗?你能说出此图形的名称吗?
导入
等腰三角形
等边三角形
一般三角形
定义类比:
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三条边都相等的三角形叫做等边三角形.
等边三角形的定义
A
B
C
等边三角形是特殊的等腰三角形.
等边三角形的定义
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形
满足什么条件的三角形是等腰三角形
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形.
方法一:从边看
方法二:从角看
方法一:
方法二:
比较
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
A
B
C
A
B
C
等边三角形的性质
A
C
B
D
E
如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.
12
针对训练
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
想一想
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
图形 等腰三角形 判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
∵ ∠A=60°,AB=BC
∴△ABC是等边三角形
等边三角形的判定
例1 如图,△ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点,且DE⊥AC,EF⊥BC,DF⊥AB,计算△DEF各个内角的度数.
解:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°.
∵DE⊥AC,EF⊥BC,DF⊥AB,
∴∠AED=∠EFC=∠FDB=90°,
∴∠ADE=90°-∠A=90°-60°=30°,
∴∠EDF=180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
即△DEF各个内角的度数都是60°.
例题
1.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
D
针对训练
2.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
A.180° B.220° C.240° D.300°
针对训练
C
3.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )
A.3 B.2 C.1 D.0
A
针对训练
例2 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ DE//BC,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
例题
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE, 求证:△ADE是等边三角形.
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ AD=AE,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ADE是等边三角形.
变式训练
例3 如图,已知△ABC是等边三角形,D为边 AC的中点,AE⊥EC,BD=EC,证明:△ADE是等边三角形.
例题
证明:∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=60°,BD⊥AC.
∵AE⊥EC,∴∠BDA=∠CEA=90°.
在Rt△ABD 和Rt△ACE中, AB=AC,
BD=CE,
∴△ABD≌△ACE,
∴AD=AE,∠EAD=∠BAD=60°,
∴△ADE是等边三角形.
例题
1.下列三角形:
①有两个角等于60°的三角形;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有( )
A.①②③ B.①②④
C.①③ D.①②③④
D
针对训练
2.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于 点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
D
针对训练
1.已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为___cm.
9
2.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
课堂练习
B
C
D
A
E
3.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
课堂练习
4.如图,A、O、D三点共线,△OAB和△OCD是两个全等的等边三角形,
求∠AEB的大小.
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A、O、D三点共线,
∴∠DOB=∠COA=120°,
∴△COA ≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
课堂练习
5.如图,已知△ABC是等边三角形,D为边 AC的中点,AE⊥EC,BD=EC,证明:△ADE是等边三角形.
证明:∵△ABC是等边三角形,D为边AC的中点,
∴AB=AC,∠BAC=60°,BD⊥AC.
∵AE⊥EC,∴∠BDA=∠CEA=90°.
在Rt△ABD 和Rt△ACE中, AB=AC,
BD=CE,
∴△ABD≌△ACE,∴AD=AE,∠EAD=∠BAD=60°,
∴△ADE是等边三角形.
课堂练习
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
总结
再 见
