吉林省长春市南关区希望高级中学2021-2022学年高一上学期期中考试数学试卷(Word版含答案)
文档属性
| 名称 | 吉林省长春市南关区希望高级中学2021-2022学年高一上学期期中考试数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 541.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-20 15:48:41 | ||
图片预览



文档简介
希望高级中学2021-2022学年高一上学期期中考试
数学
第I卷(选择题,共60分)
一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上)
1.设集合,若4∈A,则a=( )
A.-1 B.0 C.1 D.3
2.已知集合,,,则( )
A. B. C. D.
3.设m∈R,则“m>1”是“m2>1”( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.设命题,,则为( )
A., B.,
C., D.,
5.若,则下列不等式中不正确的是( )
A. B. C. D.
6.已知,,,则的最小值为( )
A.2 B.3 C. D.
7.已知,,则m等于( )
A.0 B. C. D.
8.若函数y=f(x)的定义域是[1,2021],则函数的定义域是( )
A.[0,1010] B.[0,1)∪(1,1010]
C.[0,2021] D.(0,1)∪(1,1010]
9.已知,则( )
A. B. C. D.
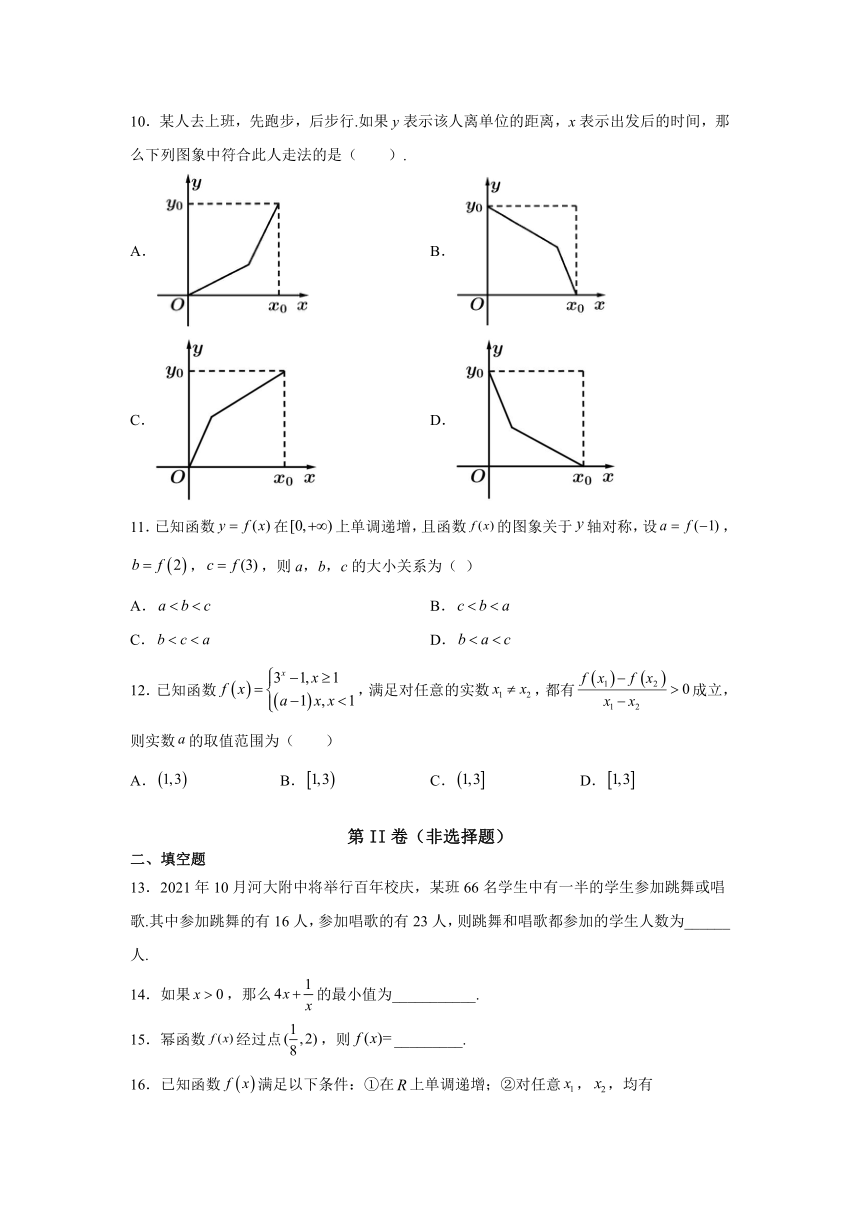
10.某人去上班,先跑步,后步行.如果y表示该人离单位的距离,x表示出发后的时间,那么下列图象中符合此人走法的是( ).
A. B.
C. D.
11.已知函数在上单调递增,且函数的图象关于轴对称,设,,,则a,b,c的大小关系为( )
A. B.
C. D.
12.已知函数,满足对任意的实数,都有成立,则实数的取值范围为( )
A. B. C. D.
第II卷(非选择题)
二、填空题
13.2021年10月河大附中将举行百年校庆,某班66名学生中有一半的学生参加跳舞或唱歌.其中参加跳舞的有16人,参加唱歌的有23人,则跳舞和唱歌都参加的学生人数为______人.
14.如果,那么的最小值为___________.
15.幂函数经过点,则_________.
16.已知函数满足以下条件:①在上单调递增;②对任意,,均有;则的一个解析式为___________.
三、解答题
17.已知集合,.
(1)当时,求,;
(2)若,求实数m的取值范围.
18.已知,,且是的必要不充分条件,求实数的取值范围.
19.某地有一座水库,设计最大容量为128000m3.根据预测,汛期时水库的进水量(单位:)与天数的关系是.水库原有水量为80000,水闸泄水量每天4000.当汛期来临第一天,水库就开始泄洪,估计汛期将持续10天,问:此期间堤坝会发生危险吗?请说明理由(水库水量超过最大容量,堤坝就会发生危险).
20.已知函数
(1)判断并证明函数的奇偶性;
(2)证明:在上为单调增函数.
21.已知函数是定义在上的偶函数,且当时,函数的解析式为.
(1)求当时,函数的解析式;
(2)求函数在区间上的值域.
22.设函数.
(1)若,求实数a的值;
(2)求证:(且);
(3)求的值.
参考答案
1.C
2.D
3.A
4.B
5.C
6.D
7.A
8.B
9.B
10.D
11.A
12.C
13.6
14.4
15.
16.,答案不唯一
17.
(1),
(2)
【分析】
(1)根据集合交集和并集的定义进行求解即可;
(2)根据集合交集的运算性质,结合子集的性质进行求解即可.
(1)
当时,可得集合,,
所以,.
(2)
由,可得,
①当时,可得,解得;
②当时,则满足,解得,
综上实数的取值范围是.
18.
【详解】
解:由,得,
或.
由,得.或
是的必要不充分条件,
则A .
19.第9天会有危险
【分析】
根据进水量与出水量,以及最多总增加水量列不等式,转化为一元二次不等式,解不等式求得第天会有危险.
【详解】
设第n天发生危险.由题意得
,
即,得.
所以汛期的第9天会有危险.
20.(1)是奇函数;
(2)证明见详解.
【分析】
(1)计算,根据奇偶性定义,判断它与的关系,从而得出结论.
(2)用定义法证明函数的单调性,按照书上例题的步骤,先从定义域中取任意两个变量,作差,比较它与零的关系,最后得出结论.
【详解】
解:(1)
定义域为:
,
即:.
所以是奇函数.
(2)证明:设,且,
有,
所以在上为单调增函数.
21.(1);(2);
【分析】
(1)由偶函数有,令即有,即可知时函数的解析式;
(2)根据函数解析式在上的单调性即可求值域.
【详解】
(1)由函数是定义在上的偶函数,即,
令,则,
∴,即,
(2)由(1)知:在上单调递减,
∴在区间上,,,故值域为.
22.(1)2(2)证明见解析 (3)0
【分析】
(1)将代入即可求值。(2)将代入化简即可得证。(3)又(2)易得
,
代入即可。
【详解】
解:(1),
.
(2),
,
(3)由(2)可知.
,…,
又,
∴
数学
第I卷(选择题,共60分)
一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上)
1.设集合,若4∈A,则a=( )
A.-1 B.0 C.1 D.3
2.已知集合,,,则( )
A. B. C. D.
3.设m∈R,则“m>1”是“m2>1”( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.设命题,,则为( )
A., B.,
C., D.,
5.若,则下列不等式中不正确的是( )
A. B. C. D.
6.已知,,,则的最小值为( )
A.2 B.3 C. D.
7.已知,,则m等于( )
A.0 B. C. D.
8.若函数y=f(x)的定义域是[1,2021],则函数的定义域是( )
A.[0,1010] B.[0,1)∪(1,1010]
C.[0,2021] D.(0,1)∪(1,1010]
9.已知,则( )
A. B. C. D.
10.某人去上班,先跑步,后步行.如果y表示该人离单位的距离,x表示出发后的时间,那么下列图象中符合此人走法的是( ).
A. B.
C. D.
11.已知函数在上单调递增,且函数的图象关于轴对称,设,,,则a,b,c的大小关系为( )
A. B.
C. D.
12.已知函数,满足对任意的实数,都有成立,则实数的取值范围为( )
A. B. C. D.
第II卷(非选择题)
二、填空题
13.2021年10月河大附中将举行百年校庆,某班66名学生中有一半的学生参加跳舞或唱歌.其中参加跳舞的有16人,参加唱歌的有23人,则跳舞和唱歌都参加的学生人数为______人.
14.如果,那么的最小值为___________.
15.幂函数经过点,则_________.
16.已知函数满足以下条件:①在上单调递增;②对任意,,均有;则的一个解析式为___________.
三、解答题
17.已知集合,.
(1)当时,求,;
(2)若,求实数m的取值范围.
18.已知,,且是的必要不充分条件,求实数的取值范围.
19.某地有一座水库,设计最大容量为128000m3.根据预测,汛期时水库的进水量(单位:)与天数的关系是.水库原有水量为80000,水闸泄水量每天4000.当汛期来临第一天,水库就开始泄洪,估计汛期将持续10天,问:此期间堤坝会发生危险吗?请说明理由(水库水量超过最大容量,堤坝就会发生危险).
20.已知函数
(1)判断并证明函数的奇偶性;
(2)证明:在上为单调增函数.
21.已知函数是定义在上的偶函数,且当时,函数的解析式为.
(1)求当时,函数的解析式;
(2)求函数在区间上的值域.
22.设函数.
(1)若,求实数a的值;
(2)求证:(且);
(3)求的值.
参考答案
1.C
2.D
3.A
4.B
5.C
6.D
7.A
8.B
9.B
10.D
11.A
12.C
13.6
14.4
15.
16.,答案不唯一
17.
(1),
(2)
【分析】
(1)根据集合交集和并集的定义进行求解即可;
(2)根据集合交集的运算性质,结合子集的性质进行求解即可.
(1)
当时,可得集合,,
所以,.
(2)
由,可得,
①当时,可得,解得;
②当时,则满足,解得,
综上实数的取值范围是.
18.
【详解】
解:由,得,
或.
由,得.或
是的必要不充分条件,
则A .
19.第9天会有危险
【分析】
根据进水量与出水量,以及最多总增加水量列不等式,转化为一元二次不等式,解不等式求得第天会有危险.
【详解】
设第n天发生危险.由题意得
,
即,得.
所以汛期的第9天会有危险.
20.(1)是奇函数;
(2)证明见详解.
【分析】
(1)计算,根据奇偶性定义,判断它与的关系,从而得出结论.
(2)用定义法证明函数的单调性,按照书上例题的步骤,先从定义域中取任意两个变量,作差,比较它与零的关系,最后得出结论.
【详解】
解:(1)
定义域为:
,
即:.
所以是奇函数.
(2)证明:设,且,
有,
所以在上为单调增函数.
21.(1);(2);
【分析】
(1)由偶函数有,令即有,即可知时函数的解析式;
(2)根据函数解析式在上的单调性即可求值域.
【详解】
(1)由函数是定义在上的偶函数,即,
令,则,
∴,即,
(2)由(1)知:在上单调递减,
∴在区间上,,,故值域为.
22.(1)2(2)证明见解析 (3)0
【分析】
(1)将代入即可求值。(2)将代入化简即可得证。(3)又(2)易得
,
代入即可。
【详解】
解:(1),
.
(2),
,
(3)由(2)可知.
,…,
又,
∴
同课章节目录
